Renormalisation - Définition

Grandeurs nues et grandeurs renormalisées

La solution a donc été de réaliser que les constantes initialement placées dans les formules de la théorie (comme par exemple l'expression du lagrangien), représentant formellement la charge électrique et la masse, ainsi que les normalisations des champs eux-mêmes, ne correspondent pas en réalité aux grandeurs physiques mesurées en laboratoire. Telles quelles, elles sont des grandeurs nues, qui ne prennent pas en compte la contribution des boucles de particules virtuelles aux grandeurs physiques mesurées. En particulier, ces effets incluent la contrepartie quantique des rétroactions électromagnétiques, qui avaient posé tant de problèmes au théoriciens de l'électromagnétisme classique. En général, ces effets sont juste aussi divergents que les amplitudes calculées. Il faut donc alors prendre des constantes nues divergentes pour obtenir des quantités mesurables finies.

Pour rendre compte de la réalité, alors, les formules doivent être réécrites en termes des quantités mesurables, renormalisées. La charge de l'électron, par exemple, doit être définie en termes d'une quantité mesurée dans des conditions cinématiques précises, le point de renormalisation, ou point de soustraction. Cette cinématique est en général caractérisée par une certaine énergie, appelée échelle de renormalisation. Les parties du lagrangien laissées de côté, qui impliquent des parties des quantités nues, peuvent alors être réinterprétées comme des contre-termes, qui, dans les diagrammes divergents, compensent exactement les divergences non-souhaitées de toutes les grandeurs calculées.

Renormalisation en QED

Par exemple, dans le lagrangien de l'électrodynamique quantique (QED),

les champs ψ_N, A_N, F_N et la constante de couplage e_N sont des grandeurs nues, d'où l'indice N. Par convention, les quantités nues sont écrites de façon à ce que les termes correspondants du lagrangien soient des multiples des termes renormalisés :

.

Fig. 5 – Le vertex correspondant au contre-terme en Z₁ qui compense la divergence du diagramme de la

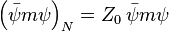
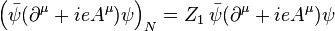
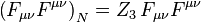Il se trouve que l'invariance de jauge, par l'intermédiaire de l'identité de Ward-Takahashi, implique que l'on peut renormaliser ensemble par la même constante les deux termes de la dérivée covariante (au sens de la théorie de jauge) , ce qui fait que l'on n'a besoin que de 3 constantes de renormalisation Z_i alors que l'on a à renormaliser 4 grandeurs : A^µ, ψ, m et e. F^µν étant une combinaison de dérivées de A^µ se renormalise de la même façon que ce dernier.

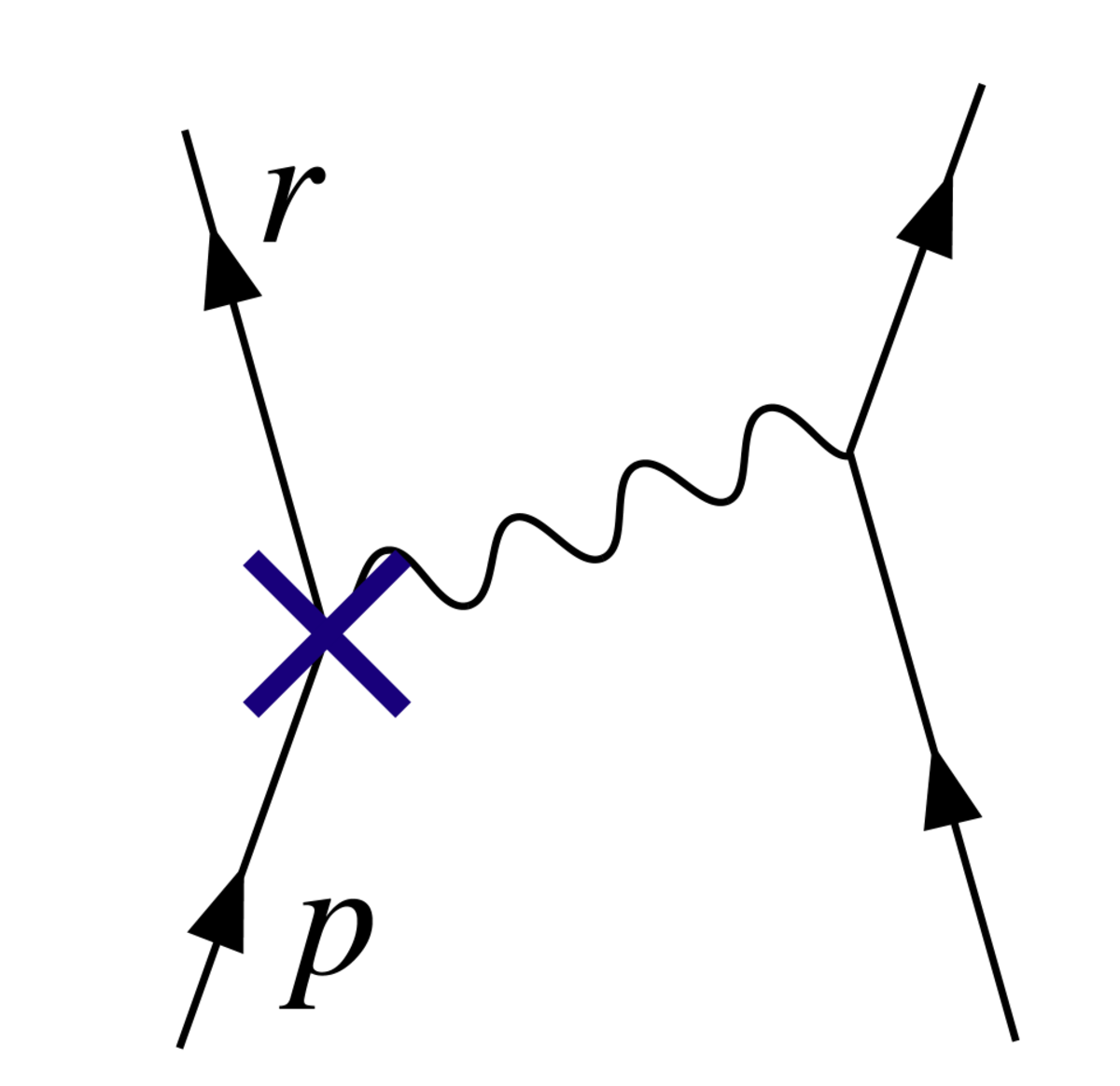
Un terme de ce lagrangien, par exemple, l'interaction électron-photon de la peut alors s'écrire :

La constante physique -e, la charge de l'électron, peut alors être définie en termes de quelque expérience donnée ; nous posons l'échelle de renormalisation à l'énergie caractéristique de cette expérience, et le premier terme représente l'interaction que nous constatons au laboratoire (à quelques petites corrections finies, provenant de diagrammes de boucles fournissant des termes exotiques comme les corrections d'ordre plus haut au moment magnétique. Le reste est le contre-terme. Avec un peu de chance, les parties divergentes des diagrammes contenant des boucles peuvent tous être décomposés en parties avec deux ou trois lignes sortantes, sous une forme algébrique qui peut être compensée par des contre-termes provenant de Z₀, Z₃ ou Z₁. En QED, la chance se concrétise : la théorie est renormalisable ().

Le diagramme avec le contre-terme de vertex en Z₁, placé comme sur la compense la divergence de la boucle de la .

La séparation des « termes nus » entre termes originaux et contre-termes a vu le jour avant l'invention du groupe de renormalisation due à Kenneth Wilson. Dans cette dernière optique, cette séparation n'a aucun caractère objectif, et est non-physique.

Variation des constantes

Pour minimiser la contribution des diagrammes de boucles à un calcul donné – et ainsi faciliter le calcul des grandeurs physiques – on choisit un point de renormalisation voisin des énergies et moments en jeu dans l'interaction que l'on veut calculer. Cependant, le point de renormalisation n'est pas lui-même une grandeur physique : les prédictions physiques de la théorie, si elles peuvent être calculées à tous les ordres, devraient en principe être indépendantes du choix de ce point, tant qu'il reste dans le domaine d'application de la théorie. Les changements d'échelle de renormalisation ne feront qu'affecter les contributions respectives des divers diagrammes de Feynman convenablement rendus finis par renormalisation. On peut exploiter ce phénomène pour calculer la variation des constantes physiques en fonction de l'échelle. Cette variation est dénotée par des fonctions β. La théorie générale de ce type de dépendance d'échelle est connue sous le nom de groupe de renormalisation.

En langage informel, les physiciens des particules parlent souvent de certaines constantes physiques qui dépendent de l'énergie de l'interaction, bien que la quantité indépendante soit en fait l'échelle de renormalisation. Cette variation décrit cependant une manière commode de décrire les changements du comportement de la théorie des champs selon les énergies impliquées dans les interactions. Par exemple, puisque la constante de couplage en QED devient petite aux grandes énergies, la théorie se comporte de plus en plus comme une théorie de particules libres, au fur et à mesure que les énergies échangées dans les interactions deviennent grandes. Ce phénomène est appelé liberté asymptotique. En choisissant une échelle d'énergie croissante, et en utilisant le groupe de renormalisaton, on peut le constater sur des diagrammes de Feynman simples. Si on ne le faisait pas, la prédiction, identique, serait bien plus difficile à faire, car elle proviendrait de compensations compliquées entre diagrammes notamment d'ordre élevé.

Pour prendre un exemple simplifié à l'extrême : l'expression est indéfinie. Pour éliminer les divergences, on peut soustraire le même contre-terme de chacun des termes. On obtient alors l'expression finie

.

On remarque qu'il aurait été bien plus commode de prendre tout de suite ε=b, ce qui aurait directement donné le résultat, le second terme s'annulant. Ce mécanisme est analogue au choix d'une échelle de renormalisation, où on n'a pas besoin de faire apparaître les compensations entre divers termes. Encore faut-il savoir que c'est la même valeur de ε qu'il faut prendre pour les deux termes. Ceci simule le rôle du groupe de renormalisation.