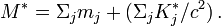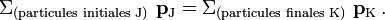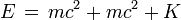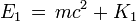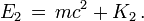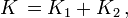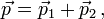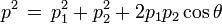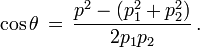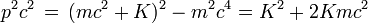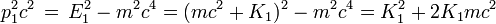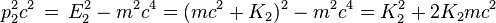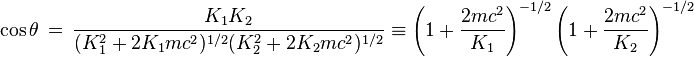Relativité restreinte - Définition

Référentiel du centre d'inertie et masse d'un système de particules

Supposons connu un système isolé et constitué de particules sans interaction, dans un référentiel R : et sont connus et restent inchangés au cours du temps, dans ce référentiel.

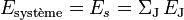
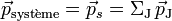
En physique classique, les définitions du centre d'inertie, et d'un référentiel inertiel où ce centre est immobile, ne posent pas de problème : on utilise les vecteurs distances et les masses des corps. En physique relativiste, une définition semblable se heurte à une difficulté de choix (faut-il choisir les masses ou les énergies ?) sans critère décisif.

La définition employée est celle qui permet d'utiliser les égalités relativistes le plus simplement : le référentiel dit « du centre d'inertie » est le référentiel R* dans lequel l'impulsion totale est nulle, soit .

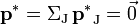
Dans ce référentiel, l'énergie E* du système vérifie l'égalité car il ne s'agit que d'un changement de référentiel, donc .

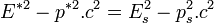
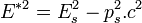
La vitesse relative entre les référentiels R et R*, notée , vérifie , mais cette vitesse est rarement utilisée dans les calculs.

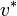
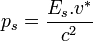
La valeur de la masse totale M* du système ainsi obtenue est indépendante du référentiel dans lequel on l'évalue : Cette invariance par rapport aux changements de référentiel, et la vérification des formules du quadrivecteur impulsion du système font que cette définition répond à toutes les propriétés attendues pour une masse.

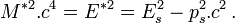
Par la conservation de l'énergie, et l'absence d'interaction (il n'y a donc pas d'énergie dans le système qui y soit consacrée), on a :

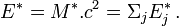
Or l'énergie E^* de chaque particule j (dans le repère R*) est la somme de l'énergie m c² correspondant à sa masse au repos m additionnée à son énergie cinétique K^* (toujours dans le repère R*), c'est-à-dire : . D'où :

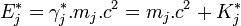
Ce qui montre que  : la masse totale d'un système de particules indépendantes est supérieure à la somme des masses individuelles des particules.

Conservation du quadrivecteur énergie-impulsion d'un système isolé

En physique classique, la quantité de mouvement et l'énergie cinétique globales d'un système isolé se conservent au cours du temps, du moins quand les chocs sont élastiques. C'est une propriété compatible mais indépendante du principe de relativité galiléen. Un changement de référentiel galiléen donne de nouvelles valeurs à l'énergie cinétique et aux cordonnées de la quantité de mouvement du système, mais ces valeurs aussi sont conservées dans le temps, dans ce référentiel.

En relativité restreinte, c'est le quadrivecteur énergie-impulsion global d'un système isolé qui se conserve, et c'est aussi une propriété compatible et indépendante du principe de relativité d'Einstein. Les coordonnées de ce vecteur à quatre dimensions (quadrivecteur) regroupe l'énergie et la quantité de mouvement, et se conservent quelleque soient les interactions entre les éléments du système isolé. De même qu'en physique non-relativiste, un changement de référentiel donne de nouvelles valeurs à l'énergie (coordonnée temporelle) et aux coordonnées de l'impulsion (coordonnées spatiales), et dans ce nouveau référentiel la conservation des valeurs de ces coordonnées, au cours du temps, est toujours valable.

Le principe de constance est le suivant :

Indépendamment des détails de l'expérience, le quadrivecteur d'un système isolé de particules se conserve dans toute interaction interne.

Autrement dit on peut écrire :

Puisque le quadrivecteur est conservé, chacune de ses composantes dans un système de référence donné (dont les valeurs dépendent du système choisi) est également conservée dans les collisions. La composante temporelle représentant l'énergie E du système et la composante spatiale représentant son impulsion , on aboutit donc pour chaque référentiel à deux lois de conservation, l'une pour l'énergie, l'autre pour la quantité de mouvement (ou impulsion).

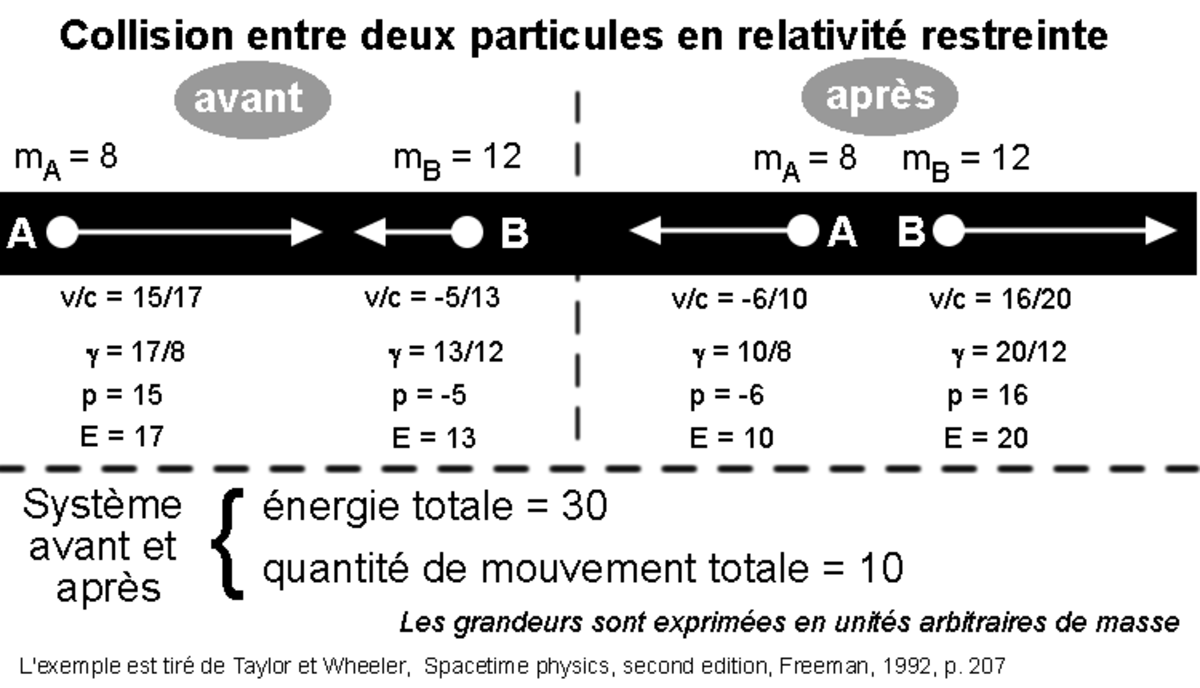
Un exemple (académique)

Une collision de deux particules est représenté dans la figure ci-contre. Une particule A de masse 8 (en unités arbitraires) animée d'une vitesse v/c de 15/17 dirigée vers la droite frappe une particule de masse 12 arrivant en sens inverse avec une vitesse v/c de 5/13 (les chiffres ont été choisis pour que les calculs "tombent juste"). Après la collision, A rebondit dans l'autre sens en ayant communiqué à B une partie de sa quantité de mouvement. L'énergie totale, somme des énergies des particules A et B est conservée, de même que la quantité de mouvement totale. Les grandeurs E et p indiquées représentent en réalité (E/c²) et (p/c) et sont exprimées en unités de masse, arbitraires. Avec ces grandeurs on a la relation E ² = p ² + m ². Le facteur γ est toujours défini par γ = [1 - (v/c)²]^-1/2.

Collision élastique

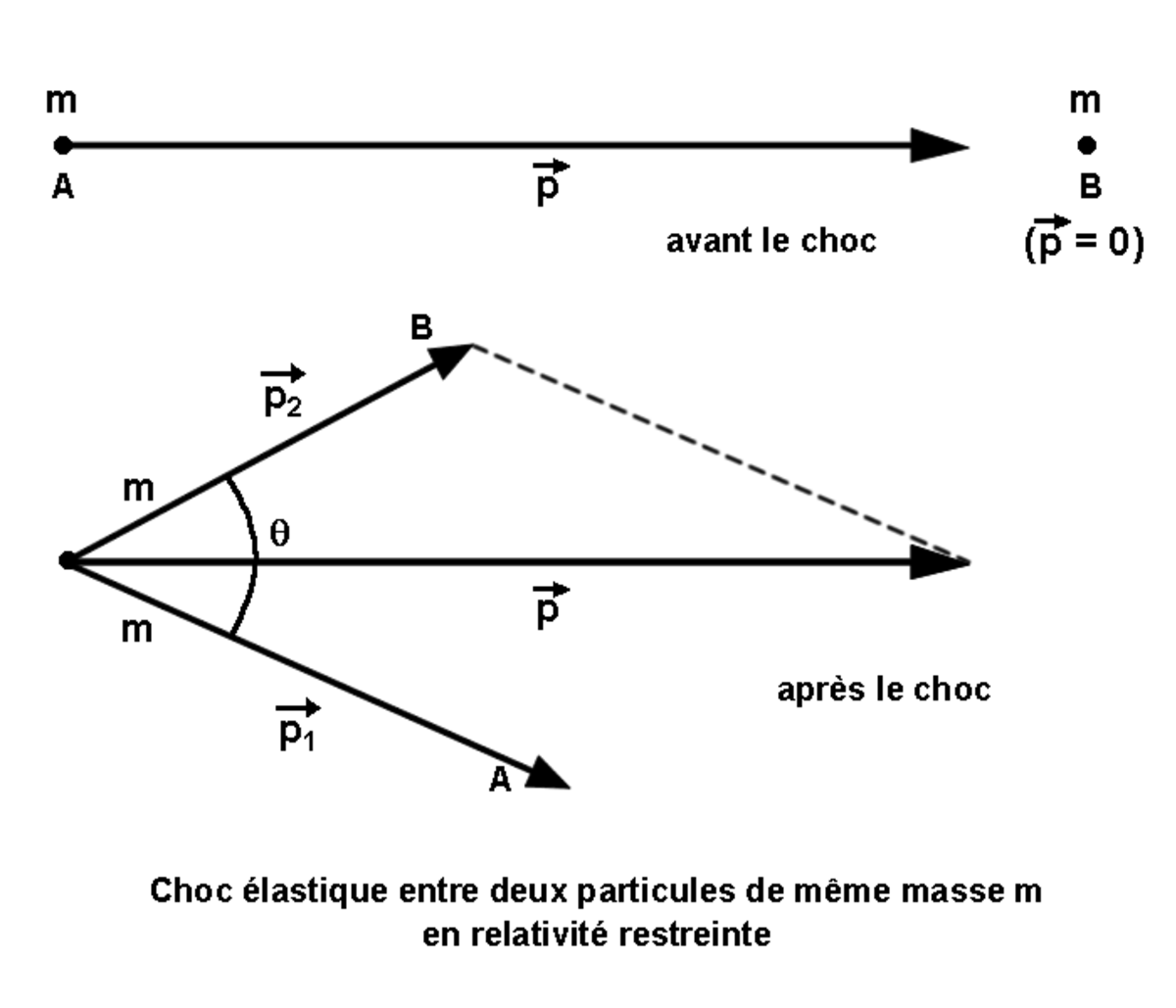
Dans un accélérateur de particules il arrive qu'une particule de très haute énergie heurte une particule au repos et communique à cette dernière une partie de son énergie cinétique. Si les seuls échanges d'énergie concernent précisément cette énergie cinétique (conservation de la quantité de mouvement du système), on dit que le choc est élastique. Les formules traduisant la conservation du quadrivecteur du système formé par ces deux particules permet d'analyser la collision. En mécanique newtonienne la direction des deux particules après un choc forme un angle droit. Ce qui n'est pas le cas dans le cas des chocs entre particules relativistes où leurs directions forment un angle aigu. Ce phénomène est parfaitement visible sur les enregistrements de collisions effectués dans des chambres à bulles.

Considérons un électron de masse m et d'énergie très élevée frappant un autre électron intialement au repos. Les vecteurs impulsions des deux particules sont tracés sur la figure ci-contre. Avant le choc l'impulsion de l'électron incident est . Après le choc, les impulsions des deux électrons sont et . En écrivant l'énergie d'un électron comme la somme de son énergie au repos mc² et de son énergie cinétique K, on peut écrire l'énergie totale du système avant la collision comme :

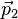
De même,

La loi de conservation de l'énergie dit que E = E + E et par conséquent

formule indiquant bien que l'énergie cinétique est conservée elle aussi (collision élastique).

La loi de conservation de la quantité de mouvement dit que

et par conséquent si nous appelons θ l'angle entre les deux vecteurs et , on a la relation

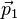
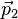
d'où l'on tire

En exprimant le carré de l'impulsion des différents électrons en fonction de leur énergie et de leur masse à l'aide des formules indiquées on obtient

pour l'électron incident et

pour les électrons après le choc.

Comme K = K + K on aboutit facilement à la formule finalement simple

Cette formule montre que cos θ est positif et donc que les directions des électrons de l'état final font entre elles un angle aigu.

On trouve facilement dans la littérature le traitement du cas où le choc est symétrique, les deux électrons possédant chacun la même énergie K = K = K/2. Dans cette situation particulière la formule générale devient

      pour une collision symétrique.

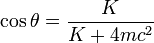
• Dans la limite newtonienne des faibles vitesses, les énergies cinétiques sont beaucoup plus petites que l'énergie au repos mc² et par conséquent

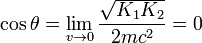
tend vers zéro, ce qui signifie que l'angle θ tend vers π /2. C'est le résultat non relativiste.

• Dans la limite au contraire des très hautes énergies, ce sont les termes d'énergie cinétique qui sont beaucoup plus grands que le terme mc² et par conséquent

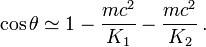
Dans ce cas le cosinus tend vers 1, ce qui signifie que l'angle entre les vitesses des électrons tend vers zéro. Cela implique un comportement complètement différent du cas newtonien.

Les formules s'appliquent évidemment au cas de la collision entre deux protons.

Diffusion Compton

Une application physique des formules de conservation de l'énergie et de la quantité de mouvement d'un système de particules est fournie par l'analyse de la collision entre un photon de haute énergie et un électron au repos, choc constituant ce que l'on appelle la diffusion Compton.