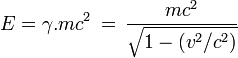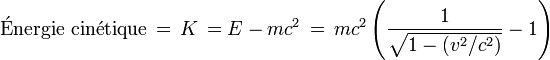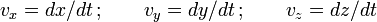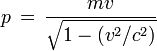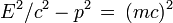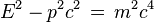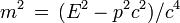Relativité restreinte - Définition
La liste des auteurs de cet article est disponible ici.
Le quadrivecteur énergie-impulsion
On peut poursuivre le raisonnement. De même que la quantité de mouvement d'une particule, dont la variation est souvent appelée à tort « impulsion » par anglicisme, était le produit « 
» de la masse par la vitesse, de même le produit « m
» du quadrivecteur vitesse « » par la masse « m » de la particule devient un quadrivecteur impulsion. On l'appelle souvent vecteur « énergie-impulsion », en exprimant ainsi le fait que énergie et impulsion (du moins quantité de mouvement) sont réunies en un concept physique de manière indissociable, de la même façon que l'espace et le temps composent l'espace-temps. En effet si les composantes spatiales de ce quadrivecteur s'identifient de façon évidente à celles d'une impulsion classique, les physiciens ont été conduits par Einstein à identifier la composante temporelle de ce quadrivecteur avec l’énergie de la particule considérée. Bien que les raisons de ce choix soient multiples, il n'est pas si facile d'en donner une véritable démonstration, mais cette situation est tout à fait courante en physique, les hypothèses naissant en même temps que la théorie se développe et que les confirmations expérimentales se succèdent. En vérité les dizaines de milliers de confirmations expérimentales quotidiennes de la théorie ainsi imaginée, sont un gage suffisant de la justesse des hypothèses qui en constituent le fondement.
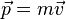
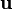
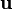
Dans un référentiel d'inertie (par exemple le référentiel terrestre en première approximation, nommé ci-après référentiel du laboratoire) les coordonnées des évènements liés à la particule suivie sont (t, x, y, z) et les composantes dans ce référentiel du quadrivecteur énergie-impulsion du mobile sont :
; avec : 
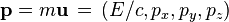
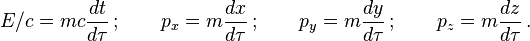
Expression relativiste de l'énergie
En tenant compte de la donnant le rapport entre le temps propre (le temps t’ de la fusée, ou τ de la particule en mouvement) et le temps t dans le référentiel considéré (référentiel du laboratoire), on a : 
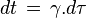
On aboutit donc à l'expression de l'énergie totale de la particule dans le référentiel du laboratoire, celui par rapport auquel la particule est animée de la vitesse 
(car l'énergie dépend du référentiel dans lequel on la calcule !) sous la forme de :
- En relativité restreinte, l'énergie totale d'une particule reste égale à la somme de l'énergie au repos m.c2 contenue dans sa masse et de l'énergie cinétique K. En tenant compte de l'expression relativiste de l'énergie, on voit que l'énergie cinétique d'une particule est donnée par l'expression :
-
- Aux "faibles" vitesses (c'est-à-dire petites devant celle de la lumière, soit tous les cas courants "classiques"), on obtient, (en première approximation) :
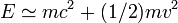
- Cette formule montre que l'énergie totale de la particule est la somme d'une énergie au repos m.c2 inconnue de la mécanique newtonienne et de l'énergie cinétique classique (1/2)m.v2 ; aux "faibles" vitesses.
-
- Pour les vitesses très proches de celle de la lumière, c'est la quantité 1 - β = [1 - (v/c)] qui compte.
- On a :
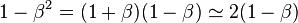
- De sorte que l'énergie totale peut alors s'écrire, (en première approximation) :
![E \simeq pc = \frac{mc^2}{\sqrt{2(1-\beta)}}\equiv \frac{mc^2}{\sqrt{2[1-(v/c)]}}](https://static.techno-science.net/illustration/Definitions/autres/6/6a958361fb5fa1bbdbc1ce7dbff8c388_7928a33011d3f35f16085f2e384a076f.png)
Expression relativiste de l'impulsion
D'autre part comme les composantes de la vitesse de la particule dans le référentiel du laboratoire sont :
En tenant compte du facteur de dilatation du temps entre dt et dτ, on arrive à l'autre formule importante fournissant la valeur de l'impulsion dans le référentiel du laboratoire :
Équivalence de l'énergie et de la masse au repos
Le quadrivecteur énergie-impulsion présente la caractéristique d'avoir sa norme, ou son carré scalaire (au sens du carré d'intervalle d'espace-temps), invariante lors d'un changement de référentiel. En bref la quantité
est indépendante du référentiel dans lequel elle est calculée. Or dans le référentiel de la particule la vitesse est nulle, de même que l'impulsion, de sorte que la norme de cette quantité invariante vaut (m c)2. Dans n'importe quel référentiel on a donc la relation capitale suivante
ou encore
(Les facteurs c qui s'introduisent dans ces formules assurent leur homogénéité, p a la grandeur de m v, E celle de m v 2.)
On peut démontrer directement cette formule à partir de donnant l'énergie et l'impulsion.
On peut faire plusieurs observations :
- (i) La valeur de l'énergie totale de la particule dépend du référentiel de l'observateur. Cependant, la valeur de l'énergie de masse est identique dans tous les référentiels, et en particulier dans le référentiel propre de la particule. C'est donc une caractéristique intrinsèque de la particule.
- (ii) Lorsque v tend vers c, γ tend vers l'infini, ce qui signifie qu'il faut une énergie infinie pour accélérer une particule jusqu'à atteindre la vitesse de la lumière. Cela est évidemment impossible. On arrive cependant à accélérer des particules à des vitesses très proches de c.
- (iii) La relativité restreinte apparaît dans tous les phénomènes physiques, même là où les vitesses intervenant ne sont pas relativistes. Un exemple flagrant est le défaut de masse de l'atome le plus simple : la masse de l'atome d'hydrogène
est inférieure à la somme des masses de l'électron et du proton d'une quantité juste égale à l'équivalent en masse de l'énergie d'ionisation de l'atome.
L’équivalence de la masse et de l'énergie est donnée par la célèbre E=mc2. Poser cette équivalence fut un pas révolutionnaire, car les concepts de matière et d'énergie étaient distincts jusque-là, bien que certains scientifiques, comme Poincaré et Lorentz, eussent indépendamment tenté le rapprochement dans le domaine de l'électromagnétisme. De nos jours, il ne faut pas non plus surestimer cette équivalence, car tandis que la masse est la norme du quadrivecteur énergie-impulsion, l'énergie n'est que l'une des composantes de ce quadrivecteur. La masse donnée par
est invariante par changement de référentiel (elle est la même dans tout référentiel). L'énergie au contraire dépend du référentiel choisi, c'est évident puisque la vitesse changeant, l'énergie cinétique change aussi.