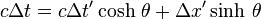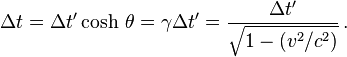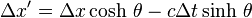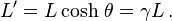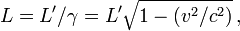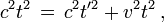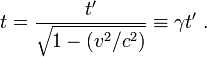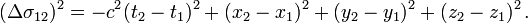Relativité restreinte - Définition
La liste des auteurs de cet article est disponible ici.
La théorie
Les postulats d'Einstein (1905)
La théorie d'Einstein est centrée sur le principe de relativité qui concerne l'observation et la mesure des phénomènes en fonction du référentiel depuis lequel l'observateur (ou l'appareil de mesure) effectue les mesures sur l'expérience.
La relativité resteinte ne considère que le cas où l'observateur est dans un référentiel inertiel, les autres référentiels sont l'objet d'étude de la relativité générale. Rappelons qu'un référentiel est dit inertiel si tout objet isolé (sur lequel ne s’exerce aucune force ou sur lequel la résultante des forces est nulle) est soit immobile, soit en mouvement de translation rectiligne uniforme. Par exemple : une fusée dans l'espace loin de toute masse constitue un référentiel inertiel si aucun moteur n'est allumé.
Les postulats de la relativité restreinte sont les suivants :
- Les lois de la physique ont la même forme dans tous les référentiels inertiels
- La vitesse de la lumière dans le vide a la même valeur dans tous les référentiels inertiels
Le premier postulat est le principe de relativité proprement dit, dans sa conception restreinte à la classe des référentiels inertiels. Il formalise un constat de Galilée selon lequel le mouvement rectiligne uniforme est « comme rien » pour l'observateur appartenant au référentiel mobile.
Le second postulat formalise l'interprétation des équations de Maxwell suivant laquelle il n'y a pas d'éther, et est conforme aux expériences. Une des conséquences est que la vitesse de la lumière est indépassable, ce qui oblige à synchroniser les horloges d'un référentiel donné par utilisation de signaux lumineux : il suffit que le « gardien du temps » émette un top horaire, disons à midi. Puis, lorsque l'observateur situé à la distance r recevra le top il tiendra compte du temps r /c que le top aura mis à lui parvenir et mettra son horloge à l'heure « midi+r /c ».
On peut se passer du second postulat pour déterminer les équations des transformations de Lorentz à condition d'introduire une hypothèse supplémentaire au premier postulat : l'espace-temps est homogène et isotrope. Ce fait a été découvert dès 1910 par Kunz et indépendamment par Comstock. L'hypothèse additionnelle conduit à un groupe de transformations, dépendant d'un paramètre c2, physiquement homogène au carré d'une vitesse. Ces transformations s'identifient aux transformations de Galilée si c2 est infini et aux transformations de Lorentz si c2 est fini positif. L'identification de c à la vitesse de la lumière, établie comme finie par les observations, se traduit par le second postulat. Jean-Marc Levy-Leblond fait remarquer que cette approche implique seulement l'existence d'une vitesse-limite c, qui est celle de toutes les particules sans masse, et donc de la lumière dans nos théories actuelles. Si le photon devait s'avérer avoir une masse (voir à ce sujet les propriétés physiques du photon), la relativité ne serait pas remise en question, mais la lumière aurait une vitesse légèrement inférieure à c, et qui dépendrait des référentiels.
Synchronisation des horloges
Plaçons nous dans une situation idéale où les difficultés techniques sont surmontées sans même y penser.
Dans le référentiel d'un observateur, étant donné une horloge immobile utilisée comme référence, il faut synchroniser une autre horloge du référentiel (c'est-à-dire une horloge immobile dans ce référentiel). Pour cela, il faut déterminer la distance entre les deux : une unité de mesure des longueurs étant connue, et sachant que la vitesse de la lumière (connue aussi, et indépassable) ne dépend pas du référentiel, il suffit de déterminer le temps mis par la lumière pour faire l'aller-retour entre les deux horloges ; mais une méthode plus manuelle peut tout aussi bien faire l'affaire. Ensuite, pour régler les deux horloges de telle sorte qu'elles aient la même unité de mesure du temps et le même temps zéro, il suffit qu'elles communiquent à la vitesse de la lumière, et, pour l'initialisation du temps zéro, que l'on tienne compte du temps mis par l'information pour aller de l'une à l'autre.
Ainsi, si un événement a lieu loin de l'horloge de référence, il peut être précisément localisé et daté par une horloge proche et immobile (dans le référentiel).
Mesure du temps et des longueurs dans les référentiels
Deux référentiels inertiels étant donnés, en translation rectiligne uniforme l'un par rapport à l'autre, comment s'assurer qu'ils ont le même système de mesure du temps et des longueurs ?
- Tout d'abord, dans un seul référentiel, les hypothèses de l'isotropie et de l'homogénéité de l'espace impliquent que les mesures que l'on peut faire sur un objet ne dépendent pas de sa position dans le référentiel.
- En transmettant des doubles de l'unité de mesure et de l'horloge de référence d'un référentiel inertiel à l'autre, on leur fait subir une accélération (pour passer de l'immobilité dans l'un à l'immobilité dans l'autre), ce qui implique que ces doubles ne sont pas dans un référentiel inertiel durant cette phase mais dans un référentiel accéléré : on peut imaginer que dans ce référentiel transitoire, leurs propriétés ne sont plus les mêmes. Mais une fois l'immobilité acquise dans le nouveau référentiel, le principe de relativité implique qu'ils ont les mêmes propriétés que dans leur précédent référentiel inertiel : les unités de mesures sont les mêmes dans les deux référentiels. Ce sera la vitesse relative entre les deux référentiels qui va donner des différences de mesures pour une même expérience.
Les transformations de Lorentz
On considère deux référentiels
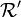




Les hypothèses d'Einstein conduisent aux transformations dites « de Lorentz ». Les formules de Lorentz permettent d'exprimer les coordonnées (x, y, z, t) d'un événement donné dans le référentiel « fixe » (disons la Terre) en fonction des coordonnées (x ’, y ’, z ’, t ’ ) du même événement dans le référentiel « mobile » (disons une fusée). Elles s'écrivent :
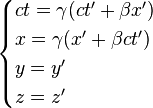
où β et γ sont des facteurs sans dimension définis par
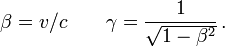
Ces expressions se simplifient et prennent une forme proche d'une rotation si on fait intervenir les fonctions hyperboliques de paramètre θ, appelé rapidité, qui est un angle de « rotation » dans l'espace de Minkowski, défini par

Avec ces notations on obtient
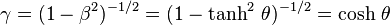
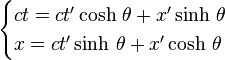
Pour obtenir les formules correspondant à la transformation inverse il suffit de changer β en -β, et donc θ en -θ.
Une recette : pour trouver le signe à mettre devant sinh θ il suffit de considérer un point au repos dans l'un des référentiels (disons celui de la fusée, avec x ’ = 0 par exemple) et de voir quel doit être le signe de la coordonnée spatiale dans l'autre référentiel (disons le référentiel fixe dans lequel x croît si la fusée a une vitesse positive).
Si les transformations spéciales simplifient l'étude analytique, elles ne nuisent en rien à la généralité. On peut aisément passer au cas où les référentiels en mouvement ne sont pas parallèles l'un à l'autre, et sont d'orientation quelconque par rapport à leur vitesse relative

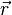
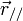
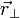
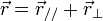
En posant
donnent :
ce qui conduit à
Comme
on a (en multipliant vectoriellement par
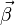
On obtient donc l'expression des transformations générales de Lorentz sous la forme :
Dilatation du temps et contraction des longueurs
Les transformations de Lorentz mènent à une vision révolutionnaire de la physique et font apparaître des phénomènes qui heurtent le sens commun.
Dans les exemples qui suivent nous allons être amenés à considérer deux événements successifs. On réécrira donc les formules précédentes en remplaçant les x et les t par des Δx et des Δt représentant l'écart spatial ou temporel entre le premier événement et le second.
Dilatation des durées
L'intervalle de temps séparant deux événements dans un référentiel est mesuré par une quantité différente dans un autre référentiel.
Considérons le référentiel terrestre constitué par un ensemble d'observateurs au repos les uns par rapport aux autres et munis d'horloges . Ces observateurs terrestres sont situés le long du trajet d'une fusée se déplaçant à la vitesse v par rapport au référentiel de la Terre. Supposons que la fusée émette un éclair toutes les secondes, le déclenchement du signal étant commandé par une horloge interne à la fusée. Dans la fusée la période de temps entre deux flashs est donc égale à 1 seconde et sera notée Δt'. Les flashs successifs étant émis au même point pour la fusée, l'intervalle spatial Δx' qui les sépare dans ce référentiel est nul. Comment la période de ces éclairs va-t-elle être perçue par les observateurs terrestres disposés le long du parcours de la fusée ?
Puisque Δx' = 0 l'équation de Lorentz
montre que l'intervalle Δt entre les éclairs successifs perçus par les observateurs liés au référentiel terrestre (et dont les horloges, rappelons-le, marquent toutes la même heure) est donné par
Cette expression indique que Δt est toujours plus grand que Δt '. Ainsi, l'intervalle de temps entre deux éclairs mesuré par 1 seconde dans le référentiel de la fusée est mesuré par γ secondes (γ > 1) dans le référentiel terrestre. On peut dire encore que les observateurs terrestres voyant l'horloge de la fusée à travers le hublot constatent que cette horloge retarde (les horloges terrestres doivent tourner γ secondes, donc plus d'une seconde, avant de voir l'horloge de la fusée tourner d'une seconde). Pour dire les choses rapidement, une horloge embarquée paraît ralentir. C'est cet effet qu'on appelle la dilatation relativiste du temps. Il est à l'origine du paradoxe des jumeaux, le jumeau revenant d'un voyage imaginaire à une vitesse proche de celle de la lumière (ce qui est évidemment technologiquement impossible à réaliser pour le moment) se retrouvant au retour plus jeune que son frère resté sur Terre, puisque son horloge de voyageur aura moins tourné que celle du sédentaire.
Considérons le cas où deux événements sont tels qu'ils se produisent en un même point de l'espace dans un certain référentiel. D'après la formule ci-dessus c'est dans ce référentiel que, lue sur une seule et même horloge, la durée mesurée est la plus courte. On lui attribue le nom de durée propre. Pour tout référentiel par rapport auquel le voyageur se déplace, la durée entre les deux mêmes événements demande, pour sa mesure, deux horloges, une en chacun des points du référentiel où se trouvera le voyageur à l'instant initial et à l'instant final. Cette durée sera toujours plus longue que la durée propre.
Les vérifications expérimentales sont nombreuses : durée de vie de atmosphériques, durée de vie de particules dans les accélérateurs, marche des horloges embarquées des satellites (le phénomène sert dans ce cas à isoler l'effet de la gravitation), etc.
Contraction des longueurs
Supposons que dans le référentiel
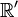
Dans le référentiel



s'écrit
Par conséquent, la longueur L mesurée sur Terre est
de sorte que L est plus petit que L’.
Il faut cependant se défendre d'appliquer ce phénomène de contraction des longueurs de façon irréfléchie. Il faut toujours passer par la définition soigneuse des événements en cause et examiner comment leurs coordonnées changent d'un référentiel à l'autre. Autrement on peut tomber sur de nombreux paradoxes. L'un des plus connus relatifs à cette contraction relativiste des longueurs est celui de la voiture censée rentrer dans un garage plus court qu'elle, à condition de rouler assez vite.
Relativité de la simultanéité
La modification de la valeur des durées entre deux événements lors du passage d'un référentiel à l'autre a souvent été exploitée dans les premières présentations de la théorie de la relativité, notamment par Einstein. En particulier la relativité limite la notion de simultanéité aux événements vus à partir d'un seul référentiel galiléen.
Deux événements simultanés dans



Illustration simple
Dans l'expérience suivante, qui illustre de façon simple la dilatation du temps prévue par la relativité restreinte, on considère une montre à photons dans laquelle un grain de lumière effectue à la vitesse c de la lumière des allers-retours entre deux miroirs.
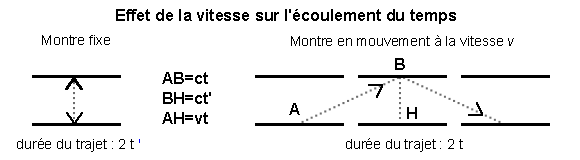
La durée d'un aller-retour dans un référentiel est égale au quotient du trajet effectué dans ce référentiel par la célérité de la lumière, laquelle ne dépend pas du référentiel. Si la montre est fixe par rapport à l'observateur, le trajet correspond à la distance au repos entre les deux miroirs et dure un temps 2t '. Si la montre se déplace par rapport à l'observateur, celui-ci verra le photon suivre une ligne brisée plus longue que le segment parcouru dans le référentiel précédent. La durée 2t du parcours est supérieure à 2t ' : la montre en mouvement retarde (il y a dilatation du temps).
La longueur de l'hypoténuse du triangle rectangle ABH de la figure est ct, celle de la hauteur est ct ' et celle de la base est vt si on note v la vitesse de translation de la montre dans le référentiel « fixe ». On a donc (théorème de Pythagore) :
d'où on tire immédiatement
On retrouve donc de façon simple la formule antérieure donnant la dilatation du temps.
La célérité de la lumière étant de 300 000 km/s, un avion volant à 0,3 km/s (soit 1000 km/h) a une vitesse égale au millionième de celle de la lumière de sorte que l'erreur commise en utilisant l'approximation galiléenne est inférieure à un millionième de millionième (soit 10-12), tout à fait négligeable dans la pratique courante. Cependant pour des mesures très précises de temps de trajets utilisées dans les expériences spatiales et aussi par le GPS, il faut impérativement tenir compte des corrections relativistes (à la fois celles de la relativité restreinte et de la relativité générale d'ailleurs).
Pour un corps se déplaçant à une vitesse égale au dixième de celle de la lumière, l'effet relativiste est de l'ordre de un pour cent. Ainsi les effets relativistes ne deviennent significatifs que pour des vitesses proches de la célérité de la lumière, impossibles à atteindre dans la vie courante (mais pas en laboratoire : les accélérateurs de particules permettent au contraire d'atteindre des vitesses allant jusqu'à quelques mètres par seconde de moins que c seulement). C'est une des raisons pour lesquelles nous avons des difficultés à appréhender concrètement le fonctionnement de la relativité restreinte.
L'intervalle d'espace-temps entre deux événements
La théorie relativiste peut donner l'impression (ne serait-ce que par son nom) de rendre les choses totalement dépendantes du référentiel (inertiel) depuis lequel sont faites les mesures. Les précédents paragraphes sur la relativité des longueurs et des durées semblent illustrer cette opinion. Pourtant ce point de vue est erroné car plus profondément la relativité restreinte s'attache au contraire à dégager ce qui est invariant par changement de coordonnées. Dans cette optique l’invariance de l'intervalle d'espace-temps entre deux événements est un élément fondateur de la théorie relativiste.
Dans un référentiel, un événement est caractérisé par ses coordonnées spatio-temporelles : « tel endroit, tel instant ». Deux événements situés respectivement en x1,y1,z1,t1 et en x2 y2, z2, t2 sont séparés par un intervalle d'espace-temps dont le carré est
Nous écrirons plus simplement
Cet intervalle est un invariant relativiste : sa valeur ne dépend pas du référentiel galiléen dans lequel on l'évalue. On peut le vérifier sur les .
Par suite de la présence du signe « - » le "carré" de l'intervalle d'espace-temps peut se révéler positif ou négatif : l'appellation de "carré" n'est que conventionnelle. C'est ce qui fait toute la différence avec le carré de la distance euclidienne, qui, elle, est toujours positive. On notera toutefois que les quantités Δt2 et Δs2 restent évidemment de « véritables » carrés, et à ce titre positifs.
Le signe de l'invariant d'espace-temps Δσ2 permet de classer deux événements l'un par rapport à l'autre, imagé par le cône de lumière, ce classement a un caractère absolu et correspond à leur possibilité ou non d'être liés par un lien causal.
Le temps et l'espace jouent des rôles symétriques dans l'intervalle d'espace-temps, et qu'il est donc logique de les mesurer de la même façon. C'est le point de vue adopté par la nouvelle définition de la vitesse de la lumière, qui, en étant fixée de manière arbitraire, établit une équivalence de fait entre longueur et temps, en redéfinissant le mètre à partir de la seconde. Concrètement on peut mesurer une distance ou un temps indifféremment en centimètres ou en secondes.
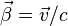
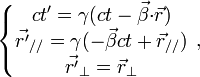
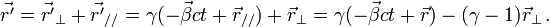
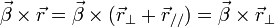
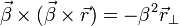
![\left\{\begin{matrix} ct'=\gamma(ct-\vec{\beta}{\cdot}\vec{r})\\ \vec{r'}=\gamma(-\vec{\beta}ct + \vec{r})+[(\gamma-1)/\beta^{2}]\,\vec{\beta}\times(\vec{\beta}\times\vec{r})\\ \end{matrix}\right.](https://static.techno-science.net/illustration/Definitions/autres/2/2722995ac8211ee563452dd9f8d60f92_fb5ce06f931f82b797555be2051f25d0.png)