Relativité générale - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Généralités - Conséquences de la théorie - Résumé de la théorie

Résumé de la théorie

Référentiels et synchronisation des horloges

L’idée centrale de la relativité est que l’on ne peut pas parler de quantités telles que la vitesse ou l’accélération sans avoir auparavant choisi un cadre de référence, un référentiel. Tout mouvement, tout événement est alors décrit relativement à ce référentiel de l'observateur.

La relativité restreinte postule que ce référentiel doit être inertiel et peut être étendu indéfiniment dans l’espace et dans le temps.

Dans le but de ne privilégier aucun type de référentiels en particulier dans l'écriture des lois de la nature (principe de covariance générale), la relativité générale traite en plus les référentiels non-inertiels, c'est-à-dire dans lesquels un corps libre de toute contrainte ne suit pas un mouvement rectiligne et uniforme. Dès lors, tout système de coordonnées est a priori admissible et, généralement, ses limites se révèlent à l'usage.

En physique classique, un exemple de référentiel non-inertiel est celui d'un véhicule qui nous transporte et qui suit un virage : la force centrifuge que l’on ressent contrarie le mouvement inertiel des corps par rapport au véhicule. Un autre exemple est le référentiel lié à la terre, qui du fait de la rotation terrestre voit se manifester la force de Coriolis bien mise en valeur par le pendule de Foucault. Une force centrifuge est dite fictive car elle n'est qu'une manifestation de l'inertie (premier principe de Newton), et non pas due à l'application d'une force.

En relativité générale, il est admis que l’on ne peut définir un référentiel que localement et sur une période finie. Cette limitation est une nécessité car elle s'impose dans plusieurs cas :

Cas le plus simple : un référentiel cartésien de l'espace en trois dimensions tournant sur lui-même autour d'un axe. L'utilisation de la relativité restreinte impose une contraction du périmètre du cercle de rotation qui aboutit à un périmètre nul à une certaine distance de l'axe de rotation. À cette distance, ce référentiel n'est plus utilisable.
L'espace s'avérant courbe, en relativité générale, l'utilisation d'un référentiel droit (utilisé pour un espace euclidien ou pseudo-euclidien, comme l'espace de Minkowski) revient à projeter cet espace sur un espace euclidien, ce qui ne peut être que localement et provisoirement possible, de la même manière, qu'à cause de la courbure de la surface terrestre, on ne peut dessiner une carte plate sans distorsion que sur une région limitée. Un exemple célèbre est la métrique de Schwarzschild qui correspond à un référentiel sphérique pseudo-euclidien à quatre dimensions (applicable sans limitation à l'espace de Minkowski), et qui n'est plus valable à l'approche du rayon de Schwarzschild.
La synchronisation des horloges se heurte à d'insurmontables difficultés : dans de nombreux cas il n'est pas possible de synchroniser parfaitement les horloges se trouvant sur un circuit fermé, ni même sur d'autres types d'axes de coordonnées car les propriétés de l'espace évoluant avec le système observé, des horloges initialement synchronisées se désynchronisent. On peut toutefois réussir cette synchronisation en plaçant l'observateur dans un référentiel synchrone (c'est-à-dire en chute libre dans le champ de gravitation) où sont choisis comme axes des géodésiques de l'espace-temps, évoluant au cours du temps de ce référentiel.

Principe d'équivalence

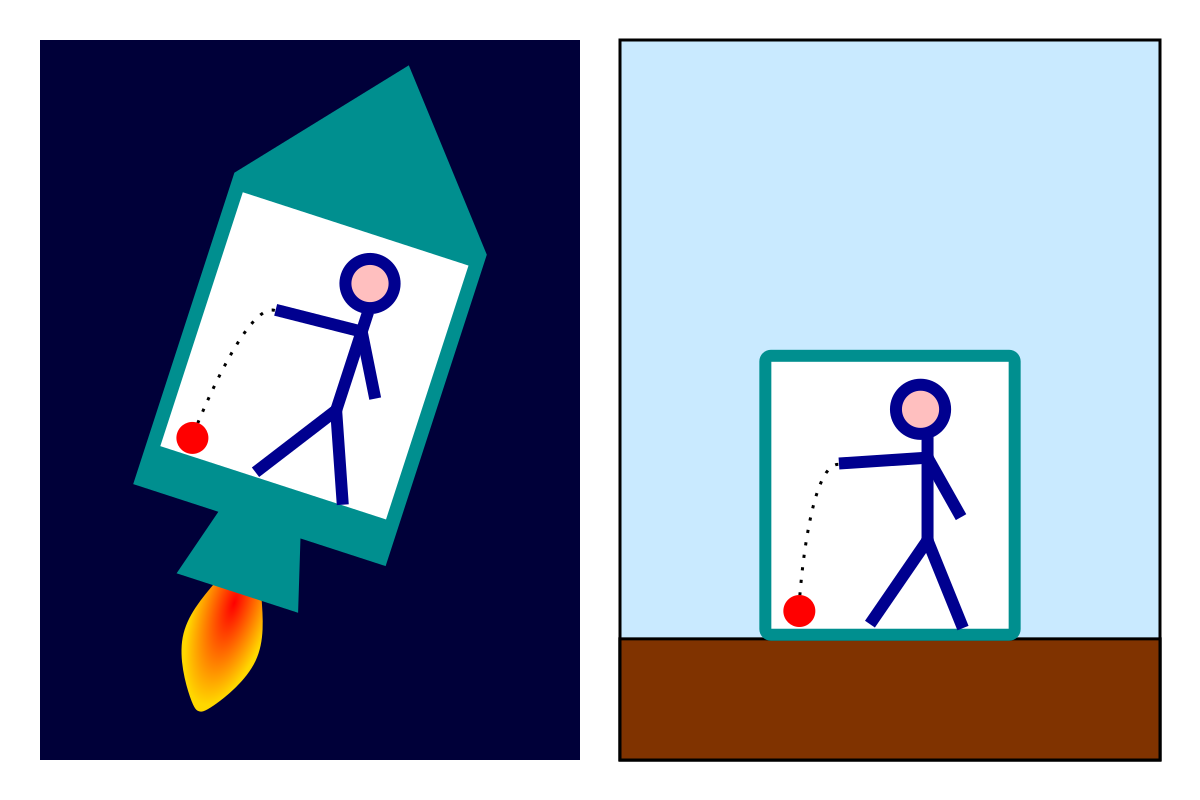
Version moderne de l'ascenseur d'Einstein : dans l'espace vide, une fusée subit une accélération constante.
La chute d'un objet vue par un observateur extérieur (à gauche), et vue par l'hôte de la fusée (à droite).

Parce qu’il n’a jamais été possible de mettre en évidence le moindre écart entre la masse d’inertie (résistance d’un corps à l’accélération) et la masse pesante (qui détermine son poids dans un champ de gravité), le principe d'équivalence en relativité générale postule qu’il n’y a pas lieu de distinguer localement un mouvement de chute libre dans un champ gravitationnel constant, d’un mouvement uniformément accéléré en l’absence de champ gravitationnel : dans les deux cas la chute d'un corps est décrite par la même loi, celle de la chute libre.

Ce résultat n’est que local, c’est-à-dire valable pour un espace restreint, « petit ». Dans un volume plus important et avec des accéléromètres sensibles, on distinguera au contraire très bien un champ de gravité (forces concourantes), une simple accélération (forces parallèles) et un effet centrifuge (forces divergentes). Mais dans un volume quasi-ponctuel, aucune mesure ne peut faire la distinction.

D'ailleurs, cette équivalence est utilisée dans le cadre de l’entraînement des astronautes : ceux-ci montent dans des avions effectuant un vol parabolique où la force centrifuge contrebalance quelques minutes les forces de gravité, simulant ainsi la « chute libre » d’un corps satellisé (mais dans ce cas la chute libre peut durer indéfiniment, puisque la trajectoire est une boucle).

Conséquences du principe d'équivalence

Principalement : existence d'un référentiel inertiel en chaque point de l'espace-temps, et détermination complète du champ de gravitation par la métrique du référentiel choisi.

En chaque point de l'espace-temps il existe un référentiel localement inertiel : un référentiel en chute libre (dans le champ de gravitation, s'il y en a) dans lequel tous les corps chutent simultanément au référentiel, si bien qu'ils ne paraissent subir aucune gravitation par rapport à ce référentiel. Par hypothèse un tel référentiel décrit un espace de Minkowski, localement. Ainsi le choix d'un référentiel fait-il disparaitre, localement, les effets de la gravitation, ou bien il en crée ; mais ces effets ne sont que locaux.
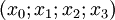
En chaque point de l'espace-temps, la gravitation est décrite comme le choix d'un référentiel non-inertiel $\ (x_0;x_1;x_2;x_3)$ , et la métrique de ce référentiel contient toutes les informations sur le champ de gravitation local.
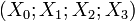
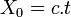
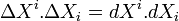
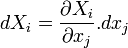
Construction de la métrique. 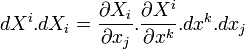Si $\ \left( X_0;X_1;X_2;X_3 \right)$ sont les coordonnées dans un référentiel inertiel local (avec, par convention, $\ X_0 = c.t$ ), la métrique de cet espace de Minkowski est notée $\ \Delta X^i.\Delta X_i = dX^i.dX_i$ , avec la convention d'Einstein, et comme $\ dX_i = \frac{\partial X_i}{ \partial x_j}.dx_j$ , on obtient comme métrique pour le référentiel non-inertiel choisi : $dX^i.dX_i = \frac{\partial X_i}{ \partial x_j}.\frac{\partial X^i}{ \partial x^k}.dx^k.dx_j$ , que l'on note aussi $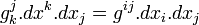g^j_k.dx^k.dx_j = g^{ij}.dx_i.dx_j$ , avec $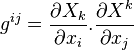g^{ij} = \frac{\partial X_k}{ \partial x_i}.\frac{\partial X^k}{ \partial x_j}$ .
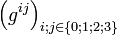
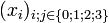
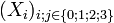
Construction du référentiel. La métrique $\left( g^{ij} \right)_{i;j \in \{0;1;2;3\} }$ étant donnée, la recherche des $\left( \frac{\partial X_i}{ \partial x_j} \right)_{i;j \in \{0;1;2;3\} }$ ne donne pas une solution unique, mais donne une infinité de solutions correspondantes, pour la moitié d'entre elles, à un changement de référentiel non-inertiel $\ (x_i)_{i;j \in \{0;1;2;3\} }$ à $\ (X_i)_{i;j \in \{0;1;2;3\} }$ inertiel ; et pour chacune de ces solutions, en connaissant un des deux référentiels on obtient l'autre par intégration.

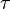
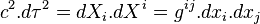
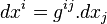
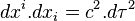
Le temps propre $\ \tau$ du référentiel inertiel (Minkowskien) vérifie $\ c^2.d\tau^2 = dX_i.dX^i = g^{ij}.dx_i.dx_j$ . En posant $\ dx^i = g^{ij}.dx_j$ , avec la convention d'Einstein, on peut écrire $\ dx^i.dx_i = c^2.d\tau^2$ .

La matrice $\left( \frac{\partial X_i}{ \partial x_j} \right)_{i;j \in \{0;1;2;3\} }$ est inversible, comme tout changement de référentiel est mathématiquement réversible.

Dérivée covariante

Cas général

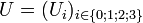
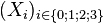
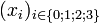
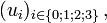
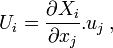
Soit un quadrivecteur $\ U = (U_i)_{i \in \{0;1;2;3\} }$ pour un référentiel (localement) inertiel $\ (X_i)_{i \in \{0;1;2;3\} }$ . Ses coordonnées dans un référentiel quelconque $\ (x_i)_{i \in \{0;1;2;3\} }$ sont $\ (u_i)_{i \in \{0;1;2;3\} } \, ,$ , avec $U_i = \frac{\partial X_i}{ \partial x_j}.u_j \, ,$ .

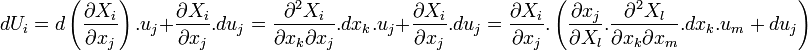
On a donc $dU_i = d \left( \frac{\partial X_i}{ \partial x_j} \right).u_j + \frac{\partial X_i}{ \partial x_j}.du_j = \frac{\partial^2 X_i}{\partial x_k \partial x_j}.dx_k.u_j + \frac{\partial X_i}{ \partial x_j}.du_j =\frac{\partial X_i}{ \partial x_j}. \left( \frac{ \partial x_j}{\partial X_l}.\frac{\partial^2 X_l}{\partial x_k \partial x_m} .dx_k.u_m + du_j \right)$ .

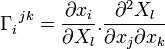
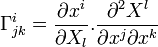
On nomme « symboles de Christoffel » les termes $\ \Gamma_i^{~jk} = \frac{ \partial x_i}{\partial X_l}.\frac{\partial^2 X_l}{\partial x_j \partial x_k}$ et $\ \Gamma^i_{jk} = \frac{ \partial x^i}{\partial X_l}.\frac{\partial^2 X^l}{\partial x^j \partial x^k}$ , qui souvent s'expriment par une formule différente mais équivalente.

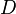
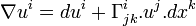
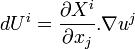
En appelant différentielle absolue ou différentielle covariante l'opérateur $\ D$ ou $\ \nabla$ défini par $\ \nabla u^i = du^i + \Gamma^i_{jk}.u^j.dx^k$ , on peut écrire $dU^i = \frac{\partial X^i}{ \partial x_j}. \nabla u^j$ .

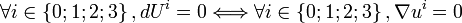
On a donc la propriété : $\forall i \in \{0;1;2;3\} \, , dU^i = 0 \Longleftrightarrow \forall i \in \{0;1;2;3\} \, , \nabla u^i = 0$ .

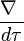
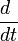
On appelle parfois principe de correspondance en relativité générale le fait de pouvoir substituer $\frac{ \nabla~}{d \tau}$ à $\frac{ d~}{dt}$ dans les équations de la physique classique pour en faire des équations de la physique relativiste, dans la mesure où des quadrivecteurs peuvent y remplacer les vecteurs.

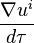
La dérivée covariante du quadri-vecteur dans le référentiel quelconque est définie par $\frac{\nabla u^i}{d \tau }$

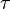
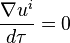
Dans le cas où, par rapport au référentiel inertiel, le quadri-vecteur est constant au cours du temps propre $\ \tau$ , on a $\frac{\nabla u^i}{d \tau } = 0$ .

Particule en chute libre

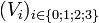
Considérons une particule de masse non-nulle mais négligeable (c'est-à-dire n'influençant pas le champ gravitationnel environnant de manière significative) en chute libre : un référentiel associé à cette particule est donc inertiel et dedans sa quadri-vitesse, de coordonnées $(V_i)_{i \in \{0;1;2;3\} }$ , y est constante.

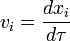
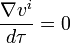
On obtient donc dans un référentiel quelconque $\ v_i = \frac{dx_i}{d \tau}$ et $\frac{\nabla v^i}{d \tau } = 0$ .

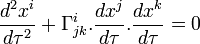
Cette équation peut aussi s'écrire $\frac{d^2x^i}{d\tau^2} + \Gamma^i_{jk}.\frac{dx^j}{d\tau}.\frac{dx^k}{d\tau} = 0$ , ce que l'on nomme aussi équation des géodésiques en relativité générale.

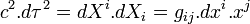
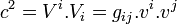
Par ailleurs, pour toute particule en chute libre, on a $\ c^2.d\tau^2 = dX^i.dX_i = g_{ij}.dx^i.x^j$ , donc $\ c^2 = V^i.V_i = g_{ij}.v^i.v^j$ : la pseudo-norme de la quadri-vitesse est égale à c dans tout référentiel.

Ces calculs n'ont pas lieu d'être pour une particule de masse nulle car son temps propre n'existe pas.

Particule de masse nulle

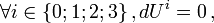
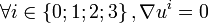
Dans le cas d'une particule de masse nulle, dont on suppose qu'elle n'influence pas le champ de gravitation environnant, on ne peut utiliser son temps propre car il n'existe pas, par contre on sait que dans un référentiel inertiel, sa vitesse est constante, donc $\forall i \in \{0;1;2;3\} \, , dU^i = 0 \, ,$ d'où $\,~\forall i \in \{0;1;2;3\} \, , \nabla u^i = 0$ .

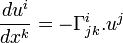
On en tire $\frac{du^i}{dx^k} = - \Gamma^i_{jk}.u^j$ . Cette égalité est d'ailleurs aussi vérifiée par les particules massives (toujours de masse négligeable) en chute libre.

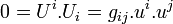
Par ailleurs, la pseudo-norme de la quadri-vitesse des particules de masse nulle est $\ 0 = U^i.U_i = g_{ij}.u^i.u^j$ dans tout référentiel.

Si la lumière est bien modélisée par des particules de masse nulle, elle subit bien la gravitation en relativité générale, suivant une même loi que les autres particules ; seules changent les coordonnées de la vitesse initiale.

Dynamique

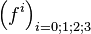
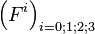
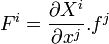
Supposons que dans un référentiel quelconque soit exercée une force relativiste, sous la forme d'un quadri-vecteur $\ \left( f^i \right)_{i =0;1;2;3}$ , sur le corps observé. Par changement de référentiel, on peut considérer cette force dans un référentiel d'inertie local par un quadri-vecteur $\ \left( F^i \right)_{i =0;1;2;3}$ tel que $\ F^i=\frac{\partial X^i}{ \partial x^j}.f^j$ .

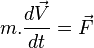
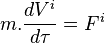
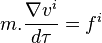
De l'égalité $m. \frac{d\vec V}{dt} = \vec F$ , en physique classique, on tire par le principe de correspondance $m.\frac{dV^i}{d\tau} = F^i$ en relativité restreinte, puis enfin $m.\frac{\nabla v^i}{d\tau} = f^i$ , équation de la dynamique relativiste en présence d'un champ de gravitation.

Tenseur d’énergie et courbure de l’espace

Mathématiquement parlant, Einstein modélise l’espace-temps par une variété pseudo-riemannienne quadri-dimensionnelle, et son équation du champ gravitationnel relie la courbure de la variété en un point, au tenseur énergie-impulsion en ce point, ce tenseur étant une mesure de la densité de matière et d’énergie (étant entendu que matière et énergie sont équivalentes).

Cette équation est à la base de la fameuse formule qui dit que la courbure de l’espace définit le mouvement de la matière, et la matière définit la courbure de l’espace (les deux étant équivalents). La meilleure façon de se représenter la géométrie de l’espace-temps est d’imaginer que celui-ci se comporte comme une surface élastique creusée localement par la présence d’un objet massif, une boule par exemple. Pour reprendre une expression célèbre due à John Archibald Wheeler : « La masse et l’énergie disent à l’espace-temps comment se courber, et la courbure de l’espace-temps dit à la matière comment se comporter ».

Tenseur d'énergie

Le tenseur d'énergie-impulsion $\ T_{ij}$ est le tenseur de densité de l'énergie et de l'impulsion de la matière répartie dans l'espace. Il généralise le quadrivecteur énergie-impulsion de la relativité restreinte : cela est rendu nécessaire par l'étude de la matière comme étendue dans l'espace.

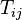
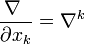
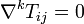
En posant $\frac{\nabla~}{\partial x_k} = \nabla^k$ , on montre que ce tenseur vérifie $\nabla^k T_{ij} = 0$ .

Courbure de l'espace-temps

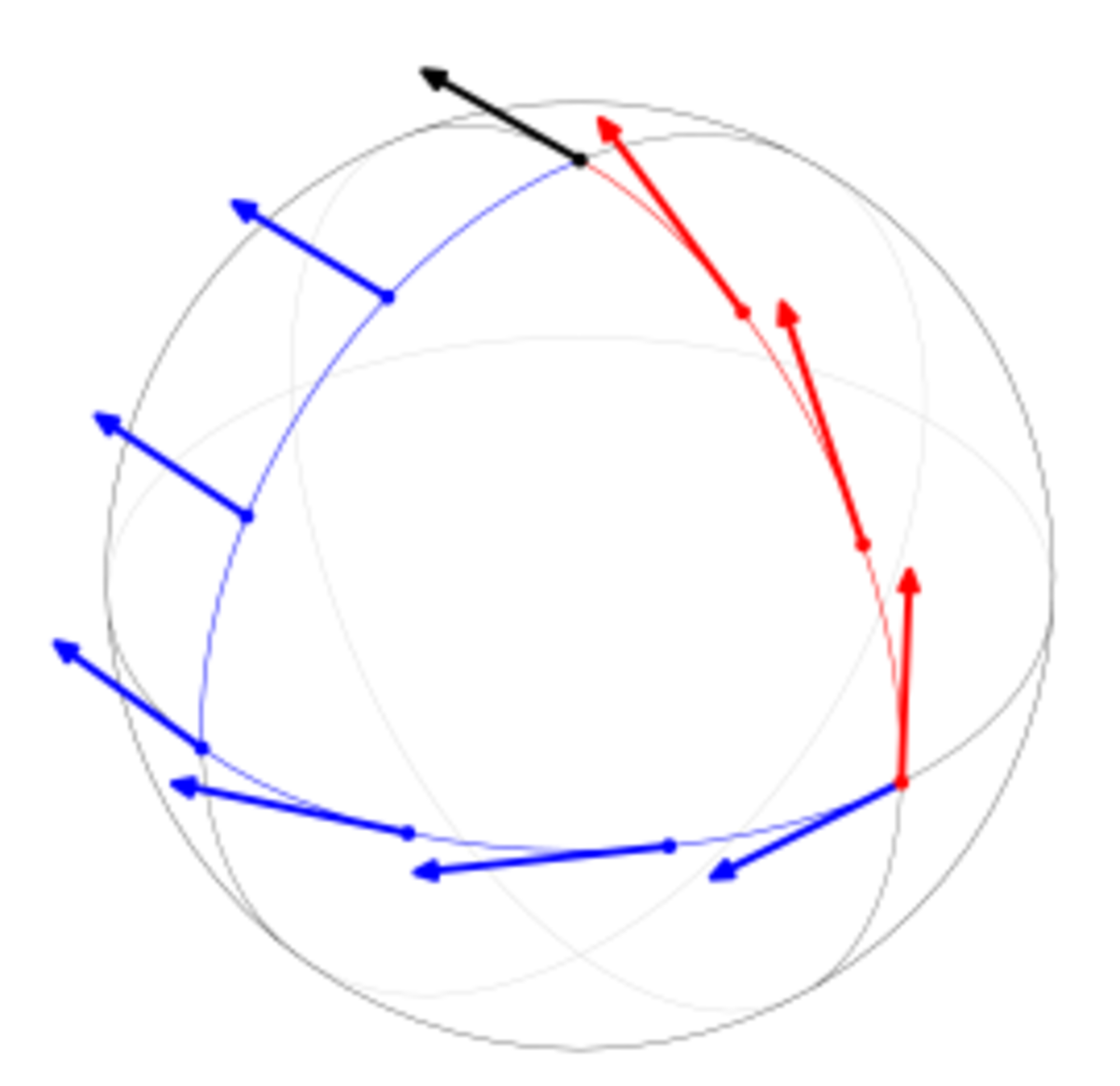
Situation visible : sur une sphère. Le vecteur tangent noir est transporté par deux chemins différents le long de géodésiques : un chemin bleu et un rouge. À l'arrivée, l'orientation du vecteur obtenu dépend du chemin : cette différence, qui n'existe pas (est nulle) en géométrie plane, est mesurée par le tenseur de Riemann-Christoffel.

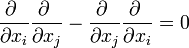
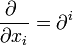
Dans un espace plat (euclidien ou pseudo-euclidien comme celui de Minkowski), le théorème de Schwarz dit que $\frac{\partial~}{\partial x_i}\frac{\partial~}{\partial x_j} - \frac{\partial~}{\partial x_j}\frac{\partial~}{\partial x_i} = 0$ , ce que l'on écrit aussi $\left[ \partial^i ; \partial^j \right] = 0$ , avec $\frac{\partial~}{\partial x_i} = \part^i$ et $\ [A;B]= A \circ B - B \circ A$ .

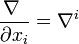
Une mesure de la courbure de l'espace est dans l'expression de $\left[ \nabla^i ; \nabla^j \right] = \frac{\nabla~}{\partial x_i}\frac{\nabla~}{\partial x_j} - \frac{\nabla~}{\partial x_j}\frac{\nabla~}{\partial x_i}$ , avec $\frac{\nabla~}{\partial x_i} = \nabla^i$ . Émerge de ces calculs un peu laborieux le tenseur de Riemann-Christoffel construit uniquement à partir de la métrique $\ g_{ij}$ .

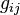
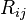
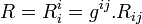
Quelques calculs supplémentaires permettent d'en tirer le tenseur de Ricci $\ R_{ij}$ . Ce tenseur vérifie un certain nombre de propriétés qui le rendent incontournable dans la recherche du lien entre la courbure de l'espace et les corps qui y sont présents. On défini aussi le scalaire nommé la courbure principale $\ R = R^i_i = g^{ij}.R_{ij}$ .

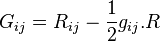
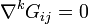
Einstein savait que le tenseur $\ G_{ij} = R_{ij}-\frac{1}{2}g_{ij}.R$ vérifie l'égalité $\nabla^k G_{ij} = 0$ , comme le tenseur énergie-impulsion.

Élie Cartan montra, après qu'Einstein ait exposé ses équations de la relativité générale, que le seul tenseur $\ G_{ij}$ non trivial, d'ordre 2, lié à la géométrie et vérifiant cette dernière égalité est bien ce tenseur, nommé maintenant le « tenseur d'Einstein ».

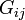
Les équations d'Einstein

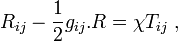
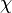
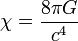
Einstein a postulé que les équations liant la matière présente et la courbure de l'espace sont $\ R_{ij}-\frac{1}{2}g_{ij}.R = \chi T_{ij} \;,$ où $\ \chi$ est une constante homogénéisant les dimensions. On détermine par l'approximation newtonienne que $\ \chi = \frac{8 \pi G}{c^4}$ .

Hilbert a justifié cette équation par le principe de moindre action dès 1915.

Dans ces équations, il s'agit de prolonger le lien créé entre la masse inertielle et l'énergie totale du corps, énoncé dans relativité restreinte, en une relation reliant la cause de la gravitation (la courbure de l'espace) à l'énergie de la matière présente.

L’équation du champ d’Einstein n’est pas linéaire, et n'a pas une solution unique. Pour la relativité générale, les lois de Newton ne sont que des approximations valables dans un référentiel local, à faible champ de gravitation et pour de petites vitesses.

La relativité générale se distingue des autres théories existantes par la simplicité du couplage entre matière et courbure géométrique, mais il reste à réaliser l’unification entre la relativité générale et la mécanique quantique, et le remplacement de l’équation du champ gravitationnel par une loi quantique plus générale. Peu de physiciens doutent qu’une telle Théorie du Tout donnerait lieu aux équations de la relativité générale dans certaines limites d’application, de la même manière que cette dernière permet de redonner la loi de la gravitation de Newton comme approximation.

Constante cosmologique et observations

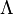
L’équation du champ peut contenir un paramètre « supplémentaire » appelé la constante cosmologique $\ \Lambda$ qui a été introduite à l’origine par Einstein pour qu’un univers statique (c’est-à-dire un univers qui n’est ni en expansion, ni en contraction) soit solution de son équation.

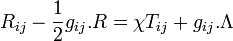
Les équations d'Einstein s'écrivent alors : $\ R_{ij}-\frac{1}{2}g_{ij}.R = \chi T_{ij} + g_{ij}.\Lambda$ .

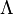
Cet effort se solda par un échec pour deux raisons : d'un point de vue théorique, l’univers statique décrit par cette théorie est instable ; et de plus les observations de l’astronome Edwin Hubble dix ans plus tard démontrèrent que l’Univers était en fait en expansion. Donc $\ \Lambda$ fut abandonnée, mais récemment, des techniques astronomiques ont montré qu’une valeur non nulle de ce paramètre est nécessaire pour expliquer certaines observations.

L’étude des solutions de l'équation d'Einstein est une branche de la physique nommée cosmologie. Elle permet notamment d’expliquer l’excès de l’avance du périhélie de Mercure, de prédire l’existence des trous noirs, des ondes gravitationnelles et d’étudier les différents scénarii d’évolution de l’Univers. Notons que l’astrophysicien bien connu Stephen Hawking a démontré qu’un univers comme le nôtre comportait nécessairement des singularités gravitationnelles.

Plus récemment (octobre 2004), des mesures effectuées par laser avec les satellites LAGEOS ont montré que le champ gravitationnel de la Terre lui-même engendre des distorsions de positionnement de la Lune de deux mètres par an comparativement à ce qui serait prévu par les seules lois de Newton. Ce chiffre est en accord à 1% près avec ce qui est prévu par la Relativité générale.

Conséquences de la théorie

- Introduction - Généralités - Conséquences de la théorie - Résumé de la théorie

Lucy survole un astéroïde en forme de cacahuète 🚀

Découverte du fossile d'un dinosaure géant méconnu 🦕

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Page générée en 0.248 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise