Relativité générale - Définition
La liste des auteurs de cet article est disponible ici.
Conséquences de la théorie
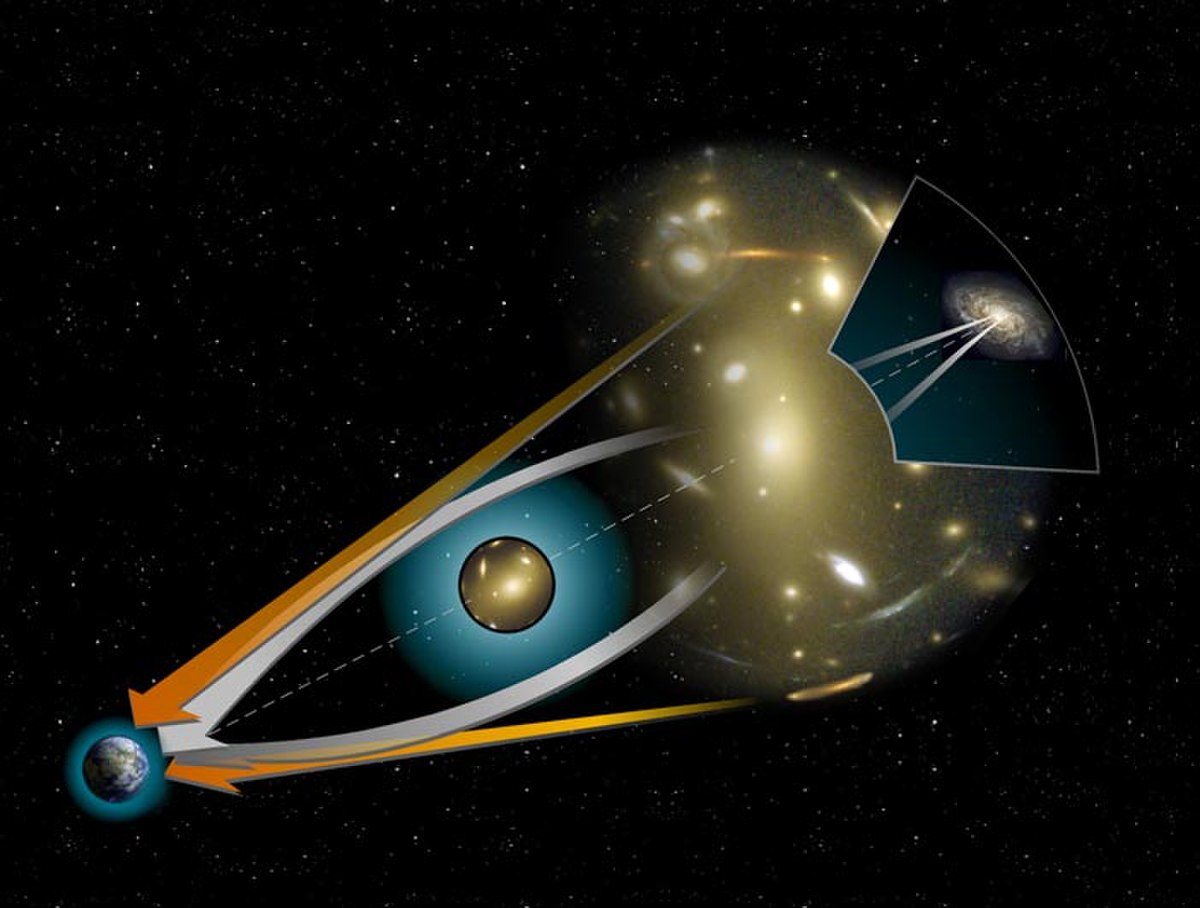
Lentille gravitationnelle
La lumière suit les géodésiques (des lignes d'espace-temps) qui sont déformées aux abords d'un corps massif par effet de la gravitation. Par conséquent, et contrairement au prévisions newtonniennes, la trajectoire de la lumière peut être fortement infléchie en présence d'un corps massif (une planète particulièrement massive) près de la trajectoire d'un rayon, et même deux rayons issus d'un même corps présent d'un côté de la planète massive, et dirigés dans des directions différentes, peuvent se rejoindre du côté opposé et créer une image dédoublée, une sorte de mirage d'origine gravitationnelle.
De tels phénomènes sont observés depuis de nombreuses années et servent notamment à la détection de la matière noire présente dans l'univers.
Trou noir
À la suite de la découverte de la métrique de Schwarzschild (1916), il est apparu dans les équations que pour toute masse sphérique il existe une distance au centre (le rayon de Schwarzschild) où des phénomènes particuliers se manifestent, si la masse est de rayon inférieur : pour un observateur un peu éloigné, les corps s'approchant de ce rayon semblent s'immobiliser, ses horloges s'arrêter et ceci pour l'éternité ; de plus, mis à part les phénomènes gravitationnels, nulle information ne semble pouvoir venir de cette masse centrale, pas même la lumière, et la masse centrale elle-même n'est décelable que par ses effets gravitationnels.
Toutefois, ce rayon de Schwarzschild n'apparut que comme une possible singularité topologique de l'espace-temps, une absurdité qui marquait une limite de la théorie, ce qui ne satisfaisait pas Einstein. Entre 1938 (Georges Lemaître) et 1939 (Robert Oppenheimer) est émise l'hypothèse que c'était un phénomène réaliste, nommé collapse gravitationnel. Dans les années 1960, la nature de ce phénomène a été précisée : il a été compris que le rayon de Schwarzschild n'est pas une singularité topologique de l'espace-temps mais seulement une singularité de la métrique utilisée due à la courbure de l'espace alors que la métrique est construite comme si l'espace était plat. Les phénomènes décrits par la métrique de Schwarzschild restent valables pour l'observateur éloigné, une métrique de Kruskal (1960) a permis de comprendre comment se fait le passage du rayon de Schwarzschild pour le voyageur.
Depuis, différents types de trous noirs ont été mis en évidence (avec ou sans charge ou moment cinétique), leur dynamique a été étudiée en détails, l'hypothèse de leur évaporation a été précisément formulée, et la notion, très hypothétique, de trou de ver a été avancée. L'observation et la détection des trous noirs est toujours l'objet de travaux intenses.
Ondes gravitationnelles
En considérant un champ de gravitation faible, la métrique
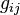
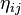
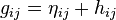
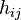
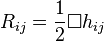

Dans le vide, l'équation d'Einstein s'écrit
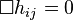
On peut de même considérer la gravitation comme une perturbation ondulatoire par rapport à une métrique quelconque non-perturbée, c'est-à-dire dans un espace-temps courbe, et on peut aussi considérer des ondes gravitationnelles de forte intensité, et étudier le rayonnement énergétique de ces ondes (en utilisant le tenseur énergie-impulsion).
La détection de telles ondes est l'objet d'intenses recherches internationales ; la petitesse des énergies mises en jeu les rendant difficilement perceptibles. La seule détection faite à ce jour est indirecte : en 1974, une perte d'énergie a été observée dans un pulsar binaire (PSR 1913+16) et a été interprétée comme due à l'émission d'ondes gravitationnelles car conforme aux prévisions faites précédemment par Thibault Damour.
La physique quantique permet d'émettre l'hypothèse qu'à cette onde est associée une particule responsable de l'interaction gravitationnelle : le graviton, de masse nulle car se déplaçant à la vitesse de la lumière dans le vide.
Modèles d'Univers
À partir des équations d'Einstein, plusieurs modèles d'Univers sont possibles. En 1915, Einstein concevait l'Univers comme stationnaire, ce que les observations cosmologiques ont contredit. Plus tard Alexandre Friedmann et Georges Lemaître ont proposé des modèles non-stationnaires : la métrique de Friedmann-Lemaître-Robertson-Walker montre que trois modèles homogènes et isotropes de l'Univers sont possibles (suivant la valeur d'un paramètre dans la métrique : espace plat, à courbure positive, ou à courbure négative). L'hypothèse de l'homogénéité et l'isotropie, qui constitue le principe cosmologique et est en accord avec les observations sur une grande échelle, implique que l'on peut choisir un temps universel tel que la métrique de l'espace soit la même à tout instant, pour tous les points et dans toutes les directions, ce qui est compatible avec la théorie du Big Bang qui prévaut actuellement.
D'autres modèles cosmologiques, plus exotiques, sont compatibles avec les équations de la relativité générale. Par exemples : l'Univers de de Sitter correspondant en physique un univers homogène, isotrope, vide de matière et ayant une constante cosmologique positive ; l'univers mixmaster qui est un univers vide de matière, homogène mais anisotrope, dont le taux d'expansion diffère dans les trois directions d'espace ; l'Univers de Gödel qui ne respecte pas le principe de causalité.
Exemples de métriques
Les équations d'Einstein sont :
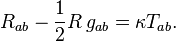
- La Métrique de Schwarzschild :Dans le vide et pour une constante cosmologique identiquement nulle, l'équation d'Einstein se réduit à :
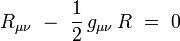
Dans le cas particulier d'un champ central engendré par un corps à symétrie sphérique, la métrique de Schwarzschild (16 janvier 1916) fournit une solution exacte à cette équation (qui n'est valide qu'à l'extérieur du corps) :
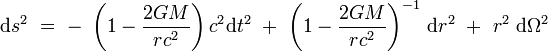
où M la masse totale du corps, et dΩ2 le carré de la distance élémentaire sur la sphère euclidienne de rayon unité en coordonnées sphériques :
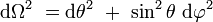
- La métrique Friedmann-Lemaître-Robertson-Walker, où l'Univers est localement homogène et isotrope.
- L'espace de Sitter correspondant en physique à un Univers vide avec constante cosmologique positive.
- L'espace anti de Sitter correspondant en physique à un Univers vide avec constante cosmologique négative.