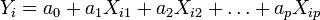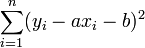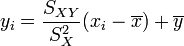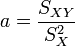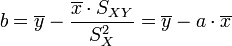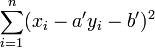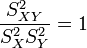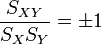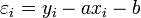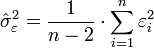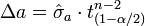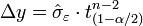Régression linéaire - Définition

Introduction

En statistiques, étant donné un échantillon aléatoire un modèle de régression simple suppose la relation affine suivante entre Y_i et X_i:

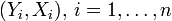
La régression linéaire consiste à déterminer une estimation des valeurs a et b et à quantifier la validité de cette relation grâce au coefficient de corrélation linéaire. La généralisation à p variables explicatives de ce modèle est donnée par

et s'appelle la régression linéaire multiple.

Situation

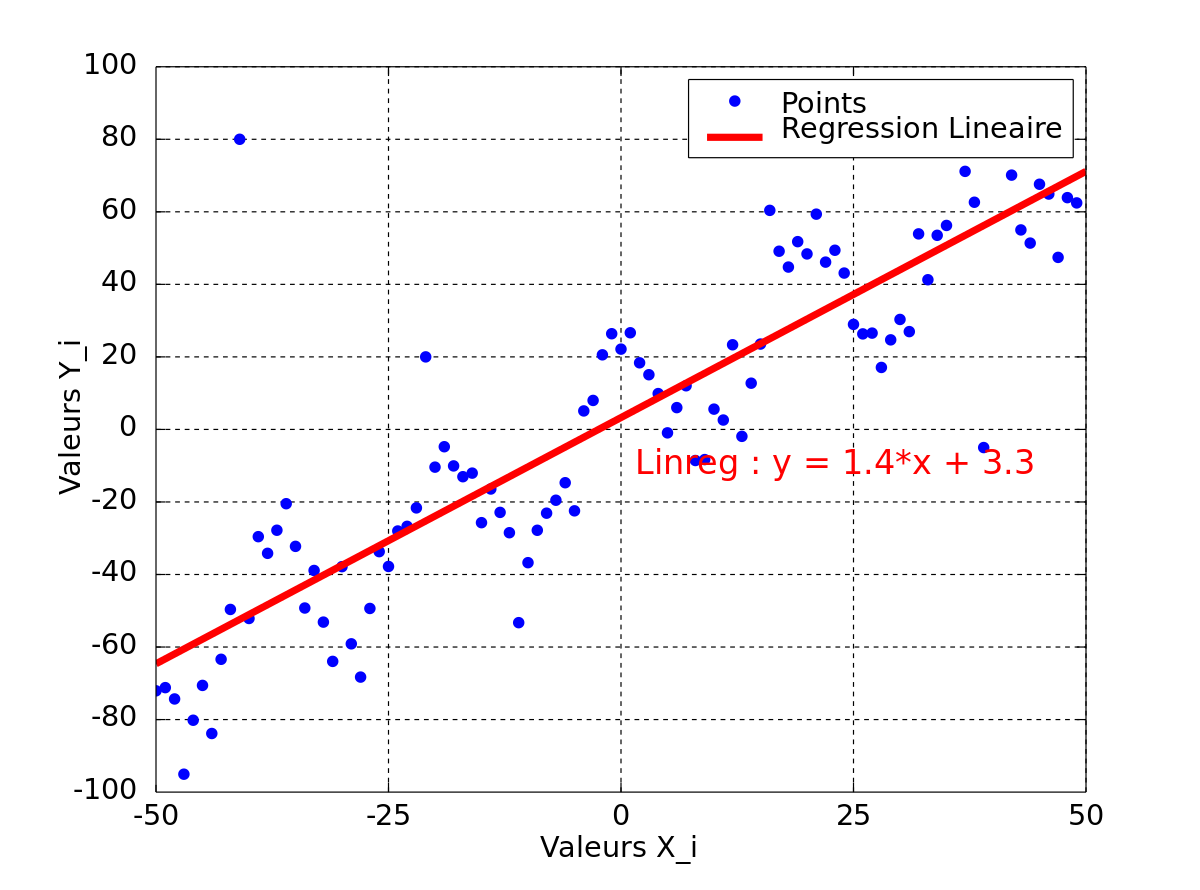
Empiriquement, à partir d'observations , on a représenté dans un graphe l'ensemble de ces points représentant des mesures d'une grandeur y_i en fonction d'une autre x_i, par exemple la taille y_i des enfants en fonction de leur âge x_i.

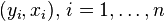
Les points paraissent alignés. On peut alors proposer un modèle linéaire, c'est-à-dire chercher la droite dont l'équation est y_i = ax_i + b et qui passe au plus près des points du graphe.

Passer au plus près, selon la méthode des moindres carrés, c'est rendre minimale la somme des carrés des écarts des points à la droite

où (y_i - ax_i - b)² représente le carré de la distance verticale du point expérimental (y_i,x_i) à la droite considérée comme la meilleure.

Cela revient donc à déterminer les valeurs des paramètres a et b (respectivement le coefficient directeur de la droite et son ordonnée à l'origine) qui minimisent la somme ci-dessus.

Résultat de la régression

La droite rendant minimale la somme précédente passe par le point G et a pour coefficient directeur . Son équation est donc :

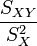
soit

Définitions

• Moyenne empirique des x_i : .
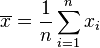
• Moyenne empirique des y_i : .
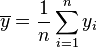
• Point moyen: .
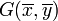
• Variance empirique des x_i : .
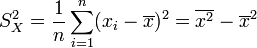
• Ecart-type empirique des x_i : .
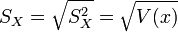
• Variance empirique des y_i : .
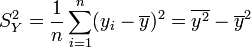
• Ecart-type empirique des y_i : .
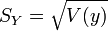
• Covariance empirique des x_i, y_i : .

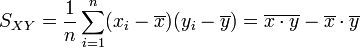
La formule de la variance se retient par la mnémonique : La moyenne des carrés moins le carré de la moyenne

de même pour la covariance : La moyenne du produit moins le produit des moyennes.

Coefficient de corrélation linéaire

On peut aussi chercher la droite D' : x = a'y + b' qui rende minimale la somme :

On trouve alors une droite qui passe aussi par le point moyen G et telle que

.

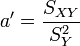
On souhaite évidemment tomber sur la même droite. Ce sera le cas si et seulement si

a' = 1/a,

c'est-à-dire si

aa' = 1.

Les droites sont confondues si et seulement si

c'est-à-dire si et seulement si

On appelle cette quantité le coefficient de corrélation linéaire entre x et y. On peut démontrer que ce nombre est toujours compris entre -1 et 1.

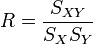
En pratique sa valeur absolue est rarement égale à 1, mais on estime généralement que l'ajustement est valide dès que ce coefficient est assez proche de 1 ou -1.

Voir également : Corrélation (mathématiques).

Erreur commise

Si l'on appelle ε_i l'écart vertical entre la droite et le point (x_i, y_i)

alors l'estimateur de la variance résiduelle σ²_ε est :

la variance de a, σ²_a, est estimée par

.

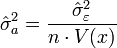
On est dans le cadre d'un test de Student sur l'espérance avec écart type inconnu. Pour un niveau de confiance α donné, on estime que l'erreur sur a est :

où t^n-2_(1-α/2) est le quantile d'ordre α/2 de la loi de Student à n-2 degrés de liberté.

L'erreur commise en remplaçant la valeur mesurée y_i par le point de la droite ax_i + b est :

À titre d'illustration, voici quelques valeurs de quantiles.

Exemples de quantiles de la loi de Student

n	niveau de confiance
	90 %	95 %	99 %	99,9 %
5	2,02	2,57	4,032	6,869
10	1,812	2,228	3,169	4,587
100	1,660	1,984	2,626	3,390

Lorsque le nombre de points est important (plus de 100), on prend souvent une erreur à 3σ, qui correspond à un niveau de confiance de 99,7 %.