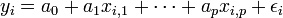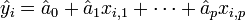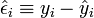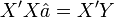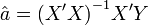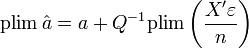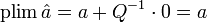Régression linéaire multiple - Définition
La liste des auteurs de cet article est disponible ici.
La méthode des moindres carrés ordinaires
Estimateur des moindres carrés ordinaires (EMCO)
Du modèle complet:
On va estimer les paramètres et obtiendra:
Les résidus estimés sont la différence entre la valeur de y observée et estimée. Soit:
Le principe des moindres carrés consiste à rechercher les valeurs des paramètres qui minimisent la somme des carrés des résidus.
-
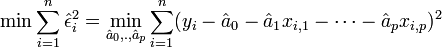
Ce qui revient à rechercher les solutions de
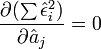
La solution obtenue est l'estimateur des moindres carrés ordinaires, il s'écrit :
Théorème —
-
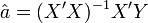
- avec X' la transposée de X
-
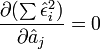
- En passant l'opérateur de dérivation dans la somme, on a
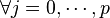
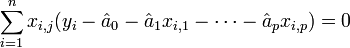
- Il suffit alors d'écrire cette dernière relation sous forme vectorielle :
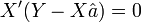
Remarques:
- Pourquoi minimiser la somme des carrés plutôt que la simple somme? Cela tient au fait que la moyenne de ces résidus sera 0, et donc que nous disposerons de résidus positifs et négatifs. Une simple somme les annulerait, ce qui n'est pas le cas avec les carrés.
- si les x j sont centrés, X 'X correspond à la matrice de variance-covariance des variables exogènes ; s'ils sont centrés et réduits, X 'X correspond à la matrice de corrélation.
Interprétation géométrique, algébrique et statistique de l'estimateur MCO
- L'estimateur MCO correspond à une projection orthogonale du vecteur Y sur l'espace formé par les vecteurs X.
- L'estimateur MCO correspond à une matrice inverse généralisée du système Y = Xa pour mettre a en évidence. En effet, si on prémultiplie par l'inverse généraliseé (X'X) − 1X' on a: (X'X) − 1X'Y = (X'X) − 1X'Xa = a
- L'estimateur MCO est identique à l'estimateur obtenu par le principe du maximum de vraisemblance.
Propriétés des estimateurs
Si les hypothèses initiales sont respectées, l'estimateur des MCO (Moindres Carrés Ordinaires) possède d'excellentes propriétés.
Propriétés en échantillons finis
Propriété — L'estimateur MCO est sans biais, c.-à-d.
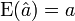
![\begin{align} \operatorname{E}[\hat a] &=\operatorname{E}\left[(X'X)^{-1}X'Y\right]\\ &= \operatorname{E}\left[a + (X'X)^{-1}X'\varepsilon\right]\\ &= a + (X'X)^{-1}X'\operatorname{E}[\varepsilon]\qquad \text{ sous } H_1 \text{ et } H_5\\ &=a+0 \qquad \qquad \qquad \qquad \text{ sous } H_2\\ &=a\end{align}](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/652c61484a82737503ef24f774b4d642_ee03bf07903cd0a9dbde8685bb900802.png)
- Cette propriété se base seulement sur les hypothèses d'espérance nulle des résidus. La présence d'autocorrélation ou d'hétéroscédasticité n'affecte pas ce résultat.
Propriété — L'estimateur MCO est le meilleur estimateur linéaire sans biais, sous les hypothèses H1 à H5
- C.-à.-d. qu'il n'existe pas d'estimateur linéaire sans biais de a qui ait une variance plus petite. Cette propriété en anglais est désignée par BLUE, pour best linear unbiased estimator. La preuve est donnée par le Théorème de Gauss-Markov.
Propriété — L'estimateur MCO est distribué selon une loi normale
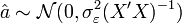
Propriétés asymptotiques
Propriété — L'estimateur MCO est convergent en probabilité, c.-à-d.
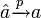
- Récrivons:
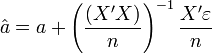
- Prenons la limite en probabilité:
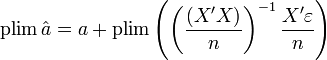
- Comme on a fait l'hypothèse H8 que
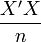
- Il reste alors à étudier le comportement de
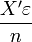
![\operatorname{E}[x_i\varepsilon_i]=0](https://static.techno-science.net/illustration/Definitions/autres/5/51a6492a30d60c2e0bf31cffb8227cf0_aafd4fd9e7ec4e09fc893bf39765ae47.png)
![\operatorname{E}[x_i\varepsilon_i]=0](https://static.techno-science.net/illustrationWebp/Definitions/autres/5/51a6492a30d60c2e0bf31cffb8227cf0_aafd4fd9e7ec4e09fc893bf39765ae47.png)
- On a donc finalement:
Propriété — L'estimateur MCO suit asymptotiquement une loi normale
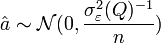
- Ce résultat est obtenu sans l'hypothèse de normalité des résidus (H6).
