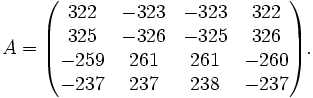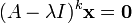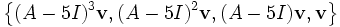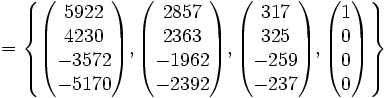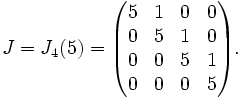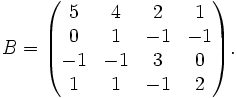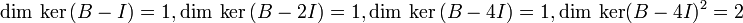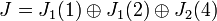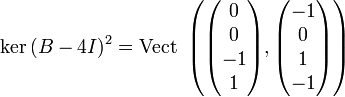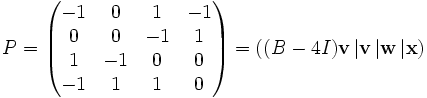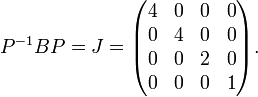Réduction de Jordan - Définition

Exemples de réduction de Jordan

Examinons les méthodes de détermination des matrices de passage par deux exemples.

Exemple 1

Déterminons la matrice de passage pour l'exemple suivant:

Recherchons les espaces caractéristiques, c’est-à-dire vecteurs x solutions de

Qui nous permettront de déterminer la suite de vecteurs dont les éléments forment les colonnes de la matrice de passage.

Remarquons alors que 5 est valeur propre et que le premier vecteur de la base de définition de la matrice possède pour polynôme minimal associé (X-5)⁴. Son espace caractéristique est donc l'espace entier. Si nous notons v ce vecteur alors, la famille composée des éléments (A − 5I)³(v), (A − 5I)²(v), (A − 5I)(v) et v forme une base de Jordan.

Nous avons déterminé la matrice de passage:

Et la matrice de Jordan est la suivante:

Exemple 2

Considérons l'exemple suivant

Les valeurs propres de B sont 4, 4, 2 et 1. De plus, on remarque que:

Nous en déduisons que l'espace vectoriel se décompose en somme directe suivante:

Nous remarquons que le vecteur colonne (0,0,−1,1)^T a pour image par la matrice (-1,0,1,-1)^T. Ces deux vecteurs colonnes engendrent l'espace caractéristique de valeur propre 4.

On en déduit

Nous en déduisons la matrice de passage et la forme de Jordan:

et

Groupe simple d'ordre 168

Il existe, à un isomorphisme près, un unique groupe simple d'ordre 168. Il peut être vu comme le groupe linéaire d'un espace vectoriel de dimension 3 sur le corps fini à deux éléments. La réduction de Jordan est une méthode pour déterminer la structure de ce groupe.