Rastérisation - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La rastérisation est un procédé qui consiste à convertir une image vectorielle en une image matricielle destinée à être affichée sur un écran ou imprimée par un matériel d'impression.
Les scènes en 3 dimensions étant généralement stockées en mémoire de manière vectorielle, ce terme s'applique également pour leur rendu à l'écran (l'écran fournissant une image matricielle), c'est d'ailleurs la principale utilisation du mot "rastérisation". Par extension, on englobe aussi dans la rastérisation tous les procédés permettant d'améliorer l'aspect final du rendu 3D.
La rastérisation d'images en deux dimensions étant nécessaire à l'intérieur de son équivalent 3D, la suite de cet article s'intéressera uniquement à la rastérisation d'images en trois dimensions dans le but de détailler les deux méthodes simultanément.
Ce procédé est l'une des deux principales techniques de rendu 3D, avec le ray tracing. Comparé au ray tracing, la rastérisation est beaucoup plus rapide en termes de calcul.
Principe géométrique de base
La conversion d'images vectorielles en trois dimensions vers une image matricielle en deux dimensions se fait en deux étapes : le conversion de l'image vectorielle 3D en image vectorielle 2D, puis la rastérisation (voir récursivité) de celle-ci en une image matricielle 2D finale.
Calcul des coordonnées 2D
La première étape est la projection des différents modèles de l'image vers le plan 2D. Ce calcul peut être résumé en trois étapes :
- l'intégration du modèle dans le monde, "Model to World" (M2W)
- la prise en compte de la position et de l'angle de la caméra, "World to Vue" (W2V)
- la prise en compte des dimensions de l'écran, "Vue to Projection" (V2P)
Chacune de ces étapes correspond à une matrice. Le calcul est une simple multiplication des coordonnées de chaque vertex avec les trois matrices. On obtient ainsi pour chaque sommet ses coordonnées 2D ainsi que sa profondeur.
Remarque : dans les APIs 3D actuelles, Direct3D utilise ces 3 matrices alors qu'OpenGL n'utilise pas la matrice monde (World) en effet, elle est combinée avec la matrice Vue donnant par conséquent une matrice "Model-Vue" (GL_MODELVIEW).
Transformation Model to World
La matrice M2W correspond à une succession d’opérations réalisées sur un objet. Ces opérations sont :
- la rotation
- la translation
- la mise à l'échelle
En terme physique on dirait qu’appliquer une matrice M2W à un objet revient à passer du référentiel propre à l’objet (le modèle) au référentiel commun à tous les objets d’une scène graphique (le monde).
-
Les matrices de rotation * Matrice de rotation dans le plan: 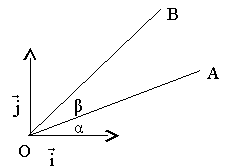
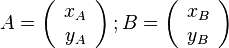
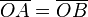
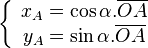
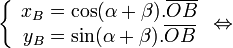
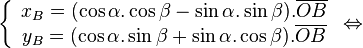
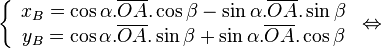
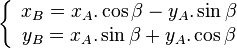
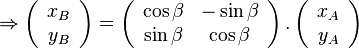
- matrices de rotation dans l'espace:
Dans un repère
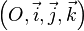
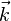
- autour de l'axe des z:
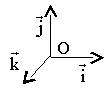
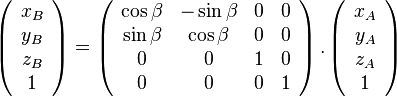
- autour de l'axe des y:
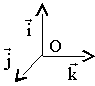
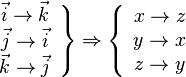
On a alors: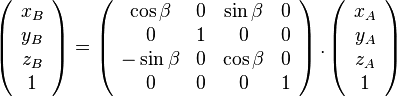
- autour de l'axe des x:
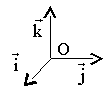
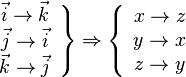
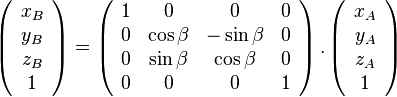
-
La matrice de translation 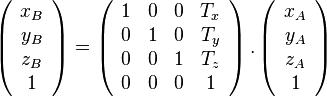
-
La matrice de mise à l'échelle 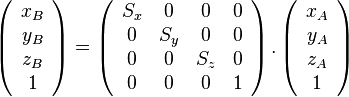
-
Synthèse M2W ![\left[ W \right] = \underbrace {\left[ T \right].\left[ {R_x } \right]....\left[ S \right].\left[ {R_z } \right].\left[ {R_y } \right]}_{M2W}.\left[ M \right]](https://static.techno-science.net/illustration/Definitions/autres/8/84477ea2ea5eebb77564cd609818176a_7b4db2ac510829a2bd5352dec269bd92.png)
- Matrices de rotation
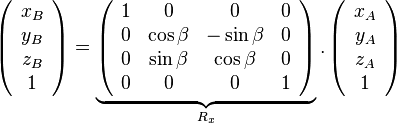
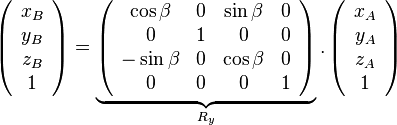
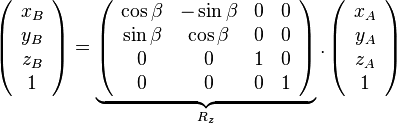
- Matrices de translation
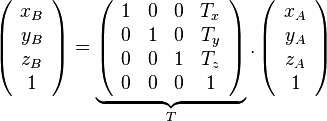
- Matrices de mise à l'échelle
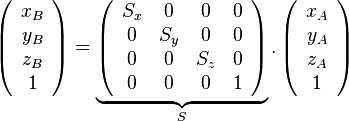
Transformation World to View
Cette matrice procède au calcul effectif des coordonnées de chaque point en fonction de la position et de la direction de la caméra.
Voici une matrice de vue classique. Pos et Dir sont les vecteurs indiquant respectivement la position de la camera et l'endroit pointé. Le vecteur Up indique la direction verticale. Up, puis F, S et U doivent tous être normalisés.
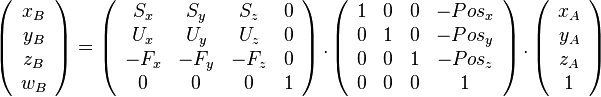
F = Pos − Dir
S = F * Up
U = S * F
Transformation View to Projection
La matrice de projection permet d'adapter les coordonnées calculées aux dimensions du framebuffer (c'est-à-dire de la fenêtre ou de l'écran). En effet une fois les coordonnées multipliées par la matrice de vue, il faut encore prendre en compte la façon dont l'observateur perçoit la scène. Il faut prendre en compte certains paramètres comme les proportions de l'image (4/3, 16/9, ou autre) ou l'angle de vision (120° dans la réalité, généralement 45° à l'écran). C'est à cela que sert cette matrice.
Filtrage des vertexes
Une fois les coordonnées 2D de chaque sommet connues, différentes techniques existent dans le but d'accélérer la suite du rendu.
Le back-face culling consiste à calculer la normale de chaque face et à la comparer avec l'orientation de la caméra. Si l'angle entre les deux est supérieur à 90°, la face est dirigée vers l'extérieur et n'a donc pas besoin d'être calculée.
Si les coordonnées 2D à l'écran de tous les sommets d'une face sont à l'extérieur de la fenêtre de vision, il n'est pas non plus nécessaire d'effectuer le reste des opérations pour celle-ci.
Rastérisation des coordonnées 2D vers l'image finale
La dernière opération est de transformer chaque face, ligne ou point en pixels à l'écran. Par exemple une ligne qui doit aller des coordonnées (2,3) à (5,3) remplira les pixels (2,3), (3,3), (4,3) et (5,3). L'opération est néanmoins nettement plus complexe pour une ligne oblique ou pour l'intérieur d'un triangle.
Pour chaque pixel ainsi calculé, il s'agit de déterminer ses caractéristiques en pondérant les valeurs aux sommets, qui, elles, sont connues. Pour reprendre l'exemple de la ligne, si le sommet à gauche est rouge et celui à droite est bleu, le premier pixel à gauche sera complètement rouge, le suivant un peu moins rouge et un peu plus bleu, et ainsi de suite jusqu'au dernier pixel qui sera complètement bleu.
Z-buffer
L'utilisation d'un z-buffer est une technique permettant de déterminer quel pixel se trouve au-dessus de quel autre. Il est en effet fréquent que deux éléments se chevauchent, et pour savoir quelles parties de quel(s) élément(s) sont visibles il est possible d'enregistrer au fur et à mesure leur profondeur dans un emplacement mémoire.
Ainsi si un pixel doit écraser un autre pixel déjà existant, on vérifie grâce au z-buffer que le premier est plus proche de la caméra que le second. Si c'est le cas, le pixel sera écrasé et le z-buffer mis à jour avec la nouvelle valeur de profondeur.
Ne pas utiliser de z-buffer signifie que les derniers éléments à être dessinés le seront forcément au-dessus des autres, même s'ils devraient normalement être en dessous.
Stencil buffer
Un stencil buffer est un tampon mémoire permettant de filtrer les endroits où l'image doit être dessinée. Le mot "stencil" signifie "pochoir" en français.
Le stencil et le z-buffer sont très liés, puisqu'il s'agit dans les deux cas de filtrer les pixels ou non. Contrairement au z-buffer, il est possible de donner l'ordre au processeur graphique de remplir le stencil buffer dans certaines conditions. L'utilisation d'un stencil buffer repose donc généralement sur deux rendus : un premier rendu partiel permettant de remplir le stencil buffer, puis un second rendu définitif où le filtrage est appliqué.
Pour des exemples pratiques, voir au bas de l'article (ombre portées et reflets).
Anticrénelage

L'anticrénelage ou anti-aliasing permet d'éviter le crénelage des lignes à l'écran. Par exemple si une ligne va des coordonnées (1,3) à (4,4) elle doit remplir entièrement les pixels (1,3) et (4,4), mais seulement partiellement les pixels (2,3), (2,4), (3,3) et (3,4).
Sans anti-crénelage, l'algorithme ne se soucie pas du remplissage partiel, ce qui créé un effet d'escalier. Avec un anti-crénelage, un remplissage partiel est effectué grâce à la moyenne pondérée de la couleur existante à cet endroit et de la nouvelle couleur.
Le FSAA ou Full Screen Anti-Aliasing consiste à appliquer l'anti-aliasing une fois l'ensemble des pixels dessinés. Il s'agit de détecter les sauts de couleurs brusques et de les atténuer en modifiant légèrement les pixels avoisinants.
Résultat final
Le résultat final est une image matricielle stockée dans un framebuffer. Cette image est alors généralement affichée à l'écran ou dans une fenêtre.

















































