Raisonnement par récurrence - Définition

Histoire

L'histoire des débuts du raisonnement par récurrence peut prêter à interprétation, suivant ce que l'on acccepte d'identifier comme tel. Si on regarde les choses d'assez loin on peut déclarer comme Jean Itard en 1961 à propos des éléments d'Euclide On ne trouvera jamais le leitmotiv moderne un peu pédant : « nous avons vérifié la propriété pour 2, nous avons montré que si elle est vraie pour un nombre, elle est vraie pour son suivant, donc elle est générale » et ceux qui ne voient l'induction complète qu'accompagnée de sa rengaine auront le droit de dire qu'on ne la trouve pas dans les Éléments. Pour nous, nous la voyons dans les prop. 3, 27 et 36, VII, 2, 4 et 13 VIII, 8 et 9 IX. Ce point de vue n'est cependant pas forcément partagé des autres historiens.

Le XVII^e siècle et ensuite

Le triangle de Pascal extrait de son manuscript. Par base Pascal entend une diagonale du triangle. Pascal se sert de la géométrie de son triangle pour en énoncer les propriétés. En termes modernes : les coefficients binômiaux sont définis par la relation  ; la conséquence XII, celle à propos de laquelle Pascal introduit la récurrence, revient à énoncer que pour tout entier p entre 1 et n, , ce que Pascal démontre par récurrence sur n. L'étape de récurrence est exposée sur un cas particulier.

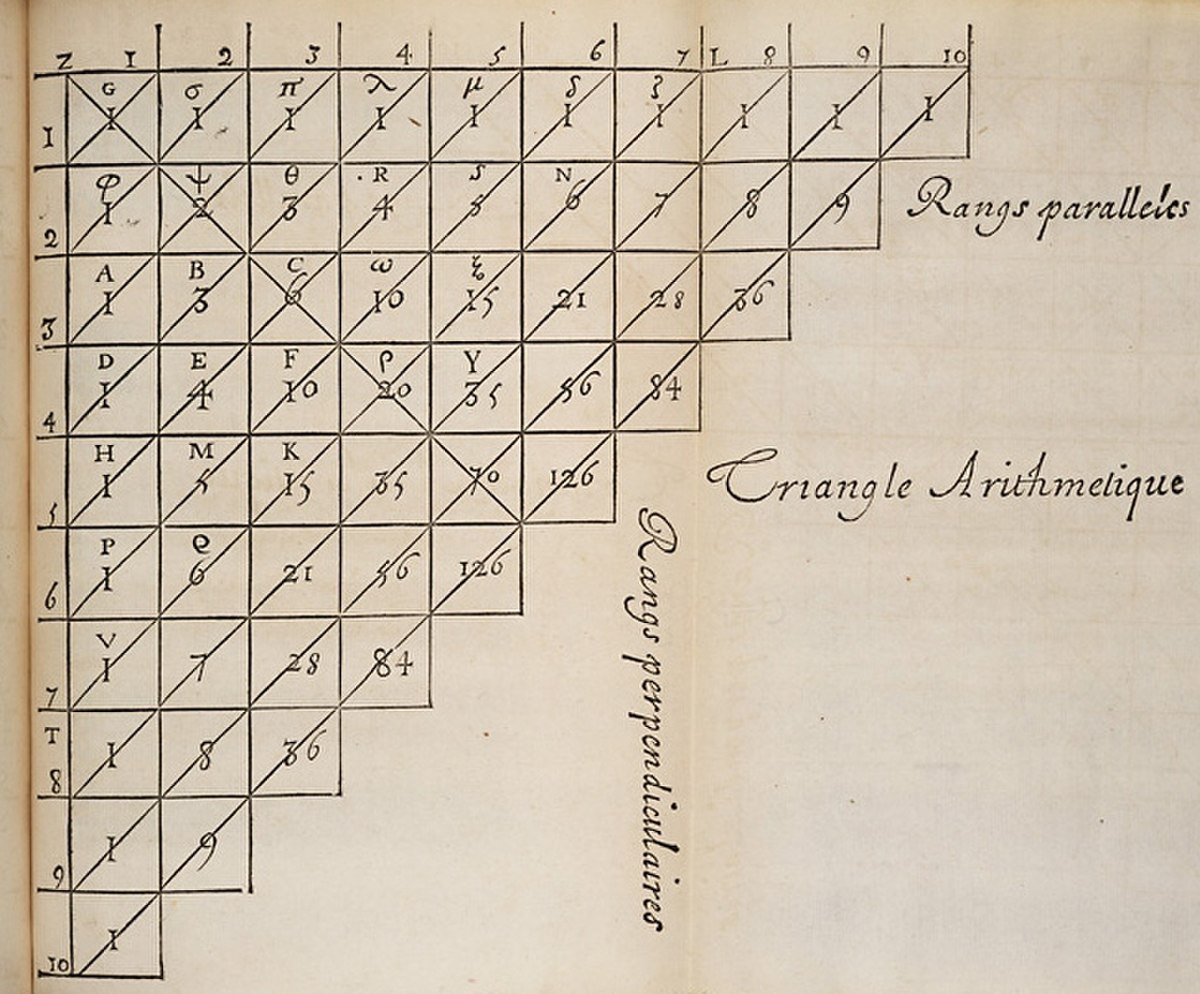
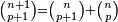
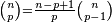
On trouve dans le Traité du triangle arithmétique de Blaise Pascal, écrit en 1654 mais publié en 1665, ce qui est généralement considéré comme la première utilisation tout à fait explicite du raisonnement par récurrence. En particulier, même si Pascal utilise parfois dans son traité des formes moins abouties, il écrit ceci :

Quoique cette proposition ait une infinité de cas, j'en donnerai une démonstration bien courte, en supposant 2 lemmes.

• Le 1, qui est évident de soi-même, que cette proportion se rencontre dans la seconde base; car il est bien visible, que φ est à σ comme 1 est à 1.
• Le 2, que si cette proportion se trouve dans une base quelconque, elle se trouvera nécessairement dans la base suivante.

D'où il se voit qu'elle est nécessairement dans toutes les bases : car elle est dans la seconde base par le premier lemme ; donc par le second elle est dans la troisième base, donc dans la quatrième, et à l'infini.

Toujours au XVII^e siècle, il faut mentionner Pierre de Fermat et Jacob Bernoulli qui critiquent tous deux la méthode d'induction de John Wallis, appelée depuis induction incomplète, qui correspond grossièrement à une démonstration pour les premiers entiers et « ainsi de suite ». Fermat promeut par ailleurs la méthode de descente infinie, liée à la récurrence (voir ci-dessous), et qu'il est le premier à identifier et nommer mais qui est déjà utilisée, là sans ambiguïté aucune, par Euclide. Mais Bernoulli propose de démontrer plutôt le passage de n à n+1, c'est-à-dire exactement le raisonnement par récurrence.

Au cours du XVIII^e et du XIX^e siècle, le raisonnement par récurrence est de plus en plus utilisé pour aboutir finalement à sa formalisation et à son axiomatisation, d'abord partiellement par Grassmann en 1861, puis par Richard Dedekind en 1888 et indépendamment par Giuseppe Peano en 1889. Pour Dedekind il s'agit d'achever l'arithmétisation des réels, en donnant un cadre formel permettant de développer la méthode des coupures publiée en 1872. Pour Peano ce sont les prémisses de son très ambitieux projet de formalisation des mathématiques (voir formulaire de mathématiques). Dans les deux cas la récurrence n'est plus simplement un principe de démonstration reposant sur l'intuition, mais un axiome formalisant une propriété des entiers naturels.

Avant le XVII^e siècle

Que Pascal soit ou non l'inventeur du raisonnement par récurrence, on ne peut négliger ses nombreux précurseurs.

Les choses se compliquent du fait de l'absence d'un langage algébrique moderne. Certains résultats ne peuvent parfois pas même être énoncés en toute généralité, et le sont donc pour des entiers donnés, alors que les idées essentielles pour la démonstration du résultat général (passage de n à n+1) sont présentes.

Florian Cajori (1918) la décèle dans la méthode cyclique de Bhaskara et dans la démonstration d'Euclide de l'existence d'une infinité de nombres premiers.

On a découvert depuis les années 1970 plusieurs formes de raisonnement par récurrence dans les mathématiques du monde arabo-islamique, voir Rashed (1972). Ainsi, vers l'an 1000, le persan Al-Karaji établit la formule du binôme de Newton (en fait il n'a pas les notations qui lui permettrait de l'énoncer dans le cas général, mais les méthodes fonctionnent pour un entier arbitraire). Il calcule également la somme des cubes des n premiers entiers naturels, al-Samaw'al poursuit ses travaux. Ces résultats utilisent bien des formes « archaïques » de définition et de raisonnement par récurrence (comme la régression, on part d'un entier donné choisi arbitrairement, et par un procédé manifestement général, en passant de n à n-1, on se ramène au cas initial). À peu près à la même époque, Ibn al-Haytham utilise le raisonnement par récurrence pour calculer la somme des cubes puis des puissances quatrièmes des n premiers entiers naturels. Bien qu'il ne mentionne même pas la possibilité d'aller au-delà de la puissance 4, sa méthode, itérative, le permettrait.

Durant le Moyen Âge européen, le philosophe et mathématicien juif languedocien Levi ben Gershom (1288-1344), dit Gersonide, fait un usage systématique de la régression pour établir des résultats de combinatoire (somme des cubes, nombre de permutations…).

Pascal, ou Bernoulli étaient déjà considérés au XIX^e siècle comme les pères du raisonnement par récurrence, mais ensuite, on a beaucoup cité pendant la première moitié du XX^e siècle le mathématicien italien Francesco Maurolico et son ouvrage Arithmeticorum libri duo (1575), ceci à la suite d'un article de G. Vacca de 1909, qui influença Moritz Cantor. et fut traduit dans d'autres langues par exemple en français en 1911. Pour démontrer que la somme des n premiers entiers impairs est un carré parfait, Maurolico utilise une proposition, qui est le passage du cas n au cas n+1 (mais celle-ci n'est pas énoncée comme un lemme, en vue de la proposition précédente). D'autre part il apparaît, d'après la correspondance de Pascal, que celui-ci a lu Maurolico. Cependant un article de Hans Freudenthal (1953), montre que Maurolico utilise dans son livre très peu de raisonnements de type récurrence (sous quelque forme que ce soit), et d'autre part les découvertes de travaux antérieurs de Al-Karaji, ben Gershom et autres relativisent fortement son apport, ceci au point que les ouvrages généralistes d'histoire des mathématiques ne le mentionnent plus.