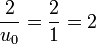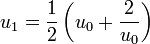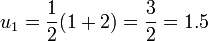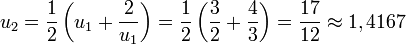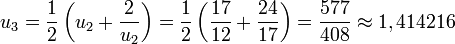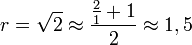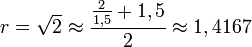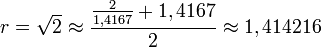Racine carrée - Définition
La liste des auteurs de cet article est disponible ici.
Racine carrée et autres structures
Si un ensemble E possède une multiplication, il peut être intéressant de se poser la question de savoir quand, pour un élément a de E, il existe un élément b tel que b2 est égal à a. Si E est égal à Z, a vérifie la propriété précédente si, et seulement si a est un carré parfait. Le terme de racine carrée sera étendu pour une raison de simplicité. La phrase 3 n'a pas de racine carrée dans Z possède un sens complètement défini.
Supposons que l'ensemble E soit égal à celui des nombres complexes, c'est-à-dire des nombres de la forme a + i.b où a et b sont des nombres réels et i l'unité imaginaire. L'unité imaginaire est un nombre dont le carré est égal à -1. Si α est un nombre complexe, alors il existe toujours un nombre complexe β tel que β2 soit égal à α. De plus, -β vérifie la même propriété. Il est fréquent de dire que β et -β sont les racines carrées de α, ce qui est tout de même plus commode que de dire que β et -β sont les racines de l'équation X2 - α = 0. On parle alors des racines carrées de α.
Par extension, et quand il n'existe pas d'ambiguité, la locution racine carrée de α où α est un élément d'un ensemble E munis d'une multiplication signifie n'importe quel élément x solution de l'équation x2 = α. La notation √α est néanmoins souvent déconseillée, elle est associée à un élément précis et non pas un ensemble.
Dans le cas des nombres réels, c'est l'article qui permet de faire la différence. Un auteur parlant d'une racine carrée de 2, traite d'un des deux éléments √2 ou bien -√2. En revanche l'expression la racine carrée de deux évoque toujours la solution positive. Comme l'expression √2 est toujours positive et le terme fonction racine définie sur les réels positifs désigne toujours la valeur positive, on évite cette confusion dans les enseignements un peu élémentaires des mathématiques en ne faisant usage que de l'expression : la racine carrée, alors toujours positive.
Extraction de racines carrées
Un premier algorithme
Nous allons exposer un algorithme qui va nous permettre d’extraire la racine carrée d’un nombre. Évidemment, si la racine carrée n’est pas un nombre décimal, alors l’algorithme ne se termine jamais, mais on s'approche autant qu'on peut le souhaiter du résultat : la suite des chiffres est exacte.
Nous commençons par séparer les chiffres du nombre par paires en commençant à partir de la virgule. Nous plaçons le nombre dont on veut extraire la racine en haut, de la même façon que lorsque nous effectuons une division selon la méthode classique ; la racine carrée sera inscrite au-dessus de ce nombre.
À chaque étape :
- on abaisse la paire de chiffres la plus significative non encore utilisée et on la place au côté d’un reste éventuel de l'étape précédente ;
- soit r le résultat intermédiaire de la racine carrée obtenu précédemment (égal à zéro au début). On cherche le plus grand chiffre x tel que le nombre y=(20r + x)x ne dépasse pas la valeur courante ;
- on place x sur la ligne supérieure au-dessus de la paire abaissée, pour former le nouveau résultat intermédiaire ;
- on soustrait y de la valeur courante pour former un nouveau reste ;
- si le reste est nul et qu’il n’y a plus de chiffre à abaisser alors l’algorithme se termine sinon on recommence.
(nota : la suite des chiffres en gras s'inscrit au fur et à mesure au-dessus du nombre initial, au-dessus de la paire de chiffre traité selon l'algorithme, et donne le résultat : 12,34 . La place de la virgule est significative mais n'a pas besoin d'être prise en compte pendant les calculs, il suffit de la constater à la fin)
1 2 3 4 01 52,27 56 1 r=0 à cette étape x=1 01 1 y=(20*0+1)1 = 1 <= 01 alors que (20*0+2)*2 = 4 > 01 donc x = 1 ____ __ j'inscris le 1: r=1 pour l'étape suivante 00 52 2x je pose 01-01=00 et j'abaisse 52: apparait 52 x=2 00 44 12 y=(20*1+2)2 = 44 <= 52 alors que (20*1+3)*3= 69 > 52 donc x = 2 _______ __ j'inscris le 2: r=12 pour l'étape suivante, 20*r = 240 08 27 24x 52-44 = 08, je pose 08 et j'abaisse 27: apparait 827 x=3 07 29 123 y=(20*12+3)*3 = 243*3 = 729 < 827 _______ __ j'inscris le 3: r=123 pour l'étape suivante, 20*r=2460 98 56 246x 827-729 = 98, je pose 98 et j'abaisse 56: apparait 9856 x=4 98 56 1234 y=(20*123+4)*4 = 9856 _______ j'inscris le 4: r=123400 -- 9856-9856 = 0 et il n'y a plus rien à abaisser : fin de l’algorithme
Vérification :
12,34 × 12,34 = 12×12 + 2×12×0,34 + 0,34×0,34. = 144 + 8,16 + (0,32×0,32 + 2×0,02×0,32 + 0,02×0,02) = 144 + 8,16 + 0,1024 + 0,0128 + 0,0004 = 152,2756
Jusqu’au XIXe siècle on utilisait couramment cet algorithme en accélérant les calculs à l’aide d’un abaque formé d’un jeu de réglettes : les bâtons de Napier.
Bien que décrite ici pour des nombres écrits en base 10, la procédure fonctionne dans n’importe quelle base, base 2 comprise. Dans ce qui précède, 20 représente le double de la base, et en binaire ce nombre serait remplacé par 100.
Par les fractions continues
Une fraction continue permet d'exprimer un nombre réel. Dans le cas particulier des racines carrés, son expression est relativement simple, ce qui permet de formuler deux méthodes d'extraction de racine. Elles possèdent toutes deux l'avantage de présenter des fractions optimales, c'est-à-dire que si p / q est une des valeurs que propose l'algorithme, alors aucune fraction de a / b avec b < q n'approche plus précisément la racine.
La deuxième méthode converge très rapidement : à chaque étape, le nombre de décimales exactes double.
La méthode de Héron
La méthode de Héron est un algorithme permettant d’approcher les racines carrées. Son importance est avant tout historique, elle a été développée par les Babyloniens. Elle fournit de bonnes approximations au prix de quelques divisions.
- Prenons la valeur rapprochée
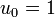
-
- On a ainsi obtenu la racine carrée de 2 à la précision 10 − 4.
On peut avoir une approche plus algorithmique en simplifiant cette méthode par la formule de Newton
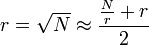
- Prenons de nouveau la valeur rapprochée
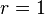
-
- On obtient la racine carrée de 2 à la précision 10 − 4.
- En appliquant cette formule on pourra écrire en langage basic :
- N = 2 /* Nombre dont on cherche la racine carrée
- r = 1 /* r = valeur rapprochée = 1
- DO /* Début de la boucle
- r = (r + (N / r)) / 2 /* Approximation
- PRINT "Racine de ";N;" ~= ";r /* Affichage du résultat
- LOOP /* Fin de la boucle
Calcul par la méthode du goutte à goutte
Les racines carrées, approximations entières
On a parfois besoin de construire des tables des parties entières des racines carrées des entiers naturels. Les premières sont données par :
| CARRE | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | .. | 15 | 16 | 17 | .. | 24 | 25 | 26 | 27 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RACINE | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | .. | 3 | 4 | 4 | .. | 4 | 5 | 5 | 5 |
Une observation des premiers termes montrent que la suite stationne d’entiers en entiers, et saute successivement d’un incrément de manière régulière. Plus précisément,
- le 0 est répété 1 fois,
- le 1, 3 fois
- le 2, 5 fois
- le 3, 7 fois
- le 4, 9 fois
Le nombre de fois que l’entier n est répété est le n-ième entier impair. La preuve repose sur l’identité suivante :
Autre méthode
Il est aisé de savoir quelle sera la taille de la racine carrée d'un nombre et cela avec un calcul élémentaire. Cela tient à la multiplication elle même: Si vous prenez le nombre de bits significatifs de deux nombres lorsque vous en faites le produit le résultat compte autant de bits que la somme des bits de chacun des opérandes. Dans le cas de la racine carrée les opérateurs sont égaux et comptent donc le même nombre de bits. En conséquence quand vous avez un nombre quelconque sa racine comporte la moitie de bits. Si vous avez un nombre de 1024 bits vous savez que la racine en aura 512. Vous pouvez donc encadrer la racine ainsi 513 bits< Racine< 511 bits
Plus loin
Mais arrivé là on peut affiner considérablement le résultat Le prodigieux algorithme du compte goutte n’est utilisable que dans son intégralité car on ne connait en principe pas la longueur de la racine. C’est désormais faux. On peut donc utiliser ce calcul pour, par exemple, les 10 premiers chiffres de la racine et ensuite compléter la valeur a 512 bits Si vous voulez extraire la racine de : 286566083047005741820534465902668361736253328912991487181716 On commence par déduire la taille de la racine qui sera donc 30 chiffres, puis on extrait les 10 premiers chiffres au compte goutte 5389438444. nous complétons la racine avec 20 fois le chiffre 9 et nous obtenons ainsi la valeur haute de la racine 538943844499999999999999999999 et en complétant avec des 0 on obtient la limite basse 53894384440000000000000000000. Vérifions:la racine étant 538943844471945205222588086383 elle est bien comprise dans notre fourchette. Plus vous calculez de chiffres au ‘compte goutte’, qui est spécialement rapide, plus vous resserrez la fourchette
Précision: Comment passer de la fourchette au résultat. 538943844499999999999999999999 538943844400000000000000000000 = 538943844471945205222588086383 ????
La solution informatique est classique ! Une simple recherche dichotomique mais au lieu de tester directement la valeur calculée avec le nombre de départ il faut l'élever au carré
function Racine_64(C: int64): int64; var a, b, d, d1: int64; begin A:= borne basse; B:= borne haute; repeat D:= (a + B) shr 1; D1:= D * D; <= on élève au carré avant de tester if D1 > C then A:= D - 1 else if C > D1 then B:= D + 1 else Result:= A; until B > A; end;
Par cette méthode, il sera possible d'extraire de nombreuses racines carrées.
Goutte à goutte
Cette méthode est utilisée pour identifier les X premiers chiffres de la racine. Mais il existe d'autres méthodes. Cherchons la racine carrée de 700528656608304465974182053402668361736253328912991487181716 On prend les 19 premiers chiffres(19 correspondant a un nombre de 64 bits) et on en extrait la racine par la classique fonction SQRT de l' ordinateur 70052865660830446 et obtenez 264675018 exactement comme avec la méthode compte goutte mais sans l'utiliser Il ne vous reste qu' mettre des 9 ou des 1 comme dans l'exemple (un décalage et un Or en informatique). On connait sans problème la longueur (voir plus haut).
Les racines n-ièmes
La solution informatique est exactement la même seul le test dans la recherche change D := (a + B) shr 1; D1 := D * D; <= on éleve au carré If suffit simplement de changer le Calcul de D1 par exponentiation désire Si vous cherchez la racine 164758 ème du nombre D1 := D * D; devient D1:=D^164758 et par approximations sucessives vous obtiendrez votre racine 164758 eme
Cette méthode présente une difficulté: si pour la racine carrée nous savons calculer rapidement la longueur (Nombre de bits div 2) Comment savoir quel sera la longueur de la racine 164758 Ce n'est en réalite sans importance et n'a quasiment aucune incidence sur le calcul Elle permet juste de gagner un ou deux cycles de la recherche dichotomie Quelques milliardièmes de secondes moyennant un calcul long informatiquement (conversion valeur ASCI et numérique) Si vous faites une recherche dichotomique pour 10 vous avez 1- 50 1- 25 1- 12 1- 6 2- 12 4- 12 8- 12 8- 12 Le calcul des racines par approximation a donc son couteau suisse: la recherche dichotomique
On peut si on le désire connaitre malgré tout la taille de la racine n° d'un nombre quelconque Sachant que pour connaitre le nombre de chiffres d'une exponentiation on utilise la formule suivante
- R := Round(A * Log10(B)) + 1;
où A est la valeur et B la puissance. Il est aisé connaissant R et B de retrouver Log10(10] une simple recherche dichotomique (encore elle) vous permettra de retrouver le log10
Et les décimales ?
Le calcul est automatique : il suffit de multiplier le nombre de départ par 10 autant de fois que vous désirez de décimales.
C'est la faute à Héron !
Bien involontaire, il faut le dire tout de suite. Dans la recherche dichotomique qu'il donne, il existe un goulet au niveau de la dichotomie elle-même : le calcul du carré (pour lui une division). C'est la plus longue, informatiquement parlant, des quatre opérations arithmétiques. Son rapport avec la multiplication est de 25, comprendre qu'il faut le même temps à un ordinateur pour faire 25 multiplications que pour faire une seule division. Toutes les recherches sur cette méthode étaient donc basées sur le gain de cycles de recherche et non sur le test lui-même.
Gagner un cycle de calcul chez Héron équivaut à en gagner 25 sur une recherche dichotomique au niveau du temps. On comprend l'incidence de la pertinence de la valeur d'initialisation.
Approximation de √a à l'aide de suites adjacentes
Soit a un nombre réel strictement positif.
Considérons les suites u et v définies par
- u(0) = 1,
- v(0) = a,
- u(n + 1) = la moyenne harmonique de u(n) et v(n) = 2 / (1 / u(n) + 1 / v(n)),
- v(n + 1) = la moyenne arithmétique de u(n) et v(n) = (u(n) + v(n)) / 2.
Les suites u(n) et v(n) sont adjacentes, et convergent vers la même limite :
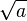
Remarquons l'originalité de cette méthode qui mêle moyennes harmonique, géométrique et arithmétique. En effet
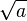
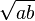
(L'intéressante moyenne arithmético-géométrique et la moyenne géométrico-harmonique sont définies par des suites similaires.)