Racine carrée de deux - Définition

Calcul babylonien

Dupliquer un carré

Construction d'un carré d'aire 2.

La question de la duplication d'un carré correspond à la construction d'un carré d'aire double de celle d'un carré donné. On suppose que l'on dispose d'un carré d'aire 1 et l'on cherche à construire un carré d'aire 2. Par définition, le carré d'aire 1 possède un côté de longueur 1 et le carré d'aire 2 possède la même aire que celle de deux carrés d'aire 1.

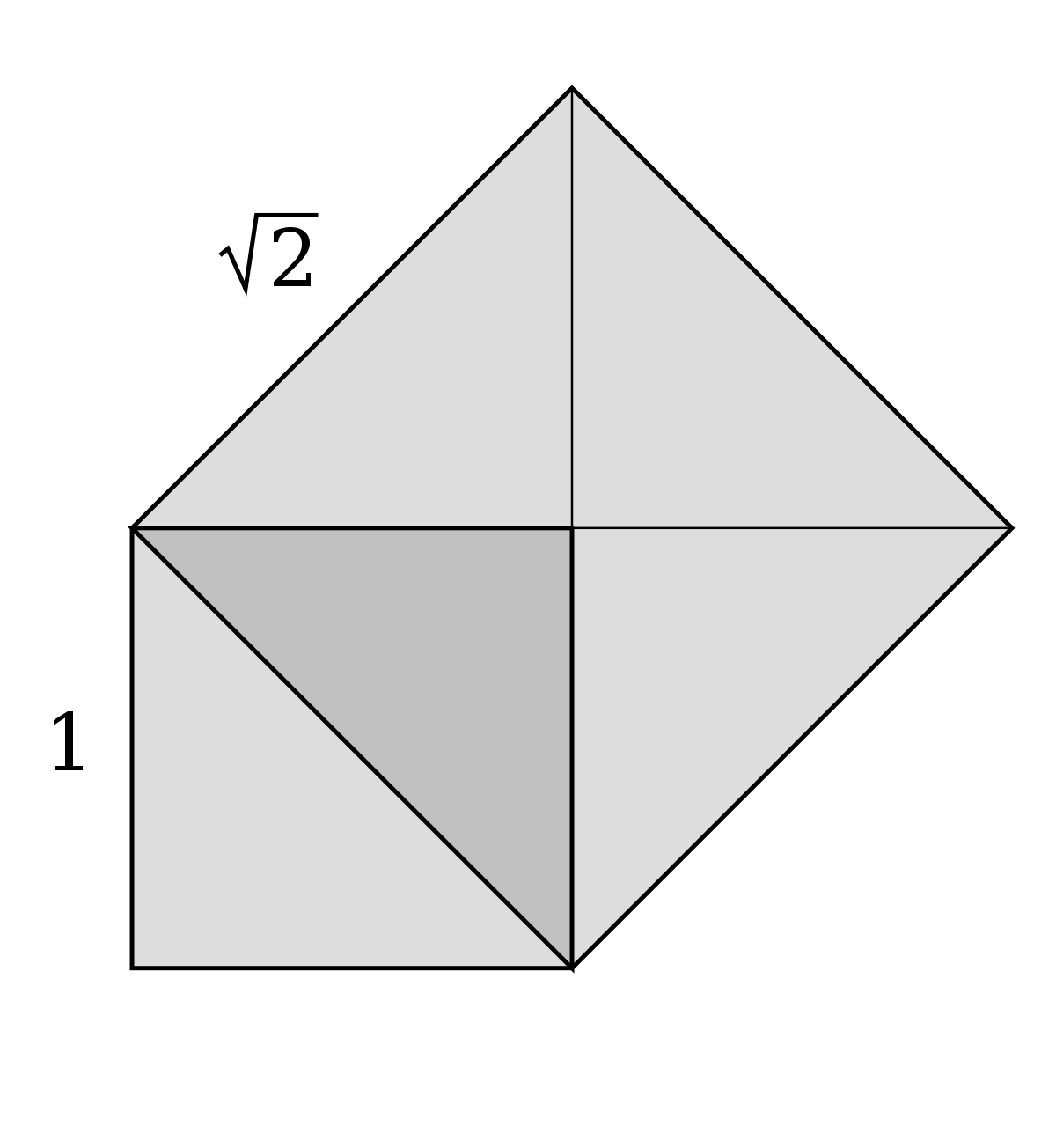
Les Babyloniens savent comment faire, ils savent même calculer le côté du carré d'aire deux avec grande précision. Il existe deux méthodes simples pour s'en persuader. La plus directe consiste à étudier la figure de gauche. Le carré de côté 1 est composé de deux triangles, celui de côté noté √2 est formé d'exactement quatre triangles du même type, il est donc d'aire double. Une autre manière de se rendre compte du rapport deux entre les aires des carrés de la figure est l'usage du théorème de Pythagore. Un triangle isocèle rectangle de petit côté de longueur 1 possède une hypoténuse de carré égal à 1 + 1 = 2. Cette hypoténuse est la diagonale d'un carré de côté de longueur 1.

Duplication du carré grâce au cercle

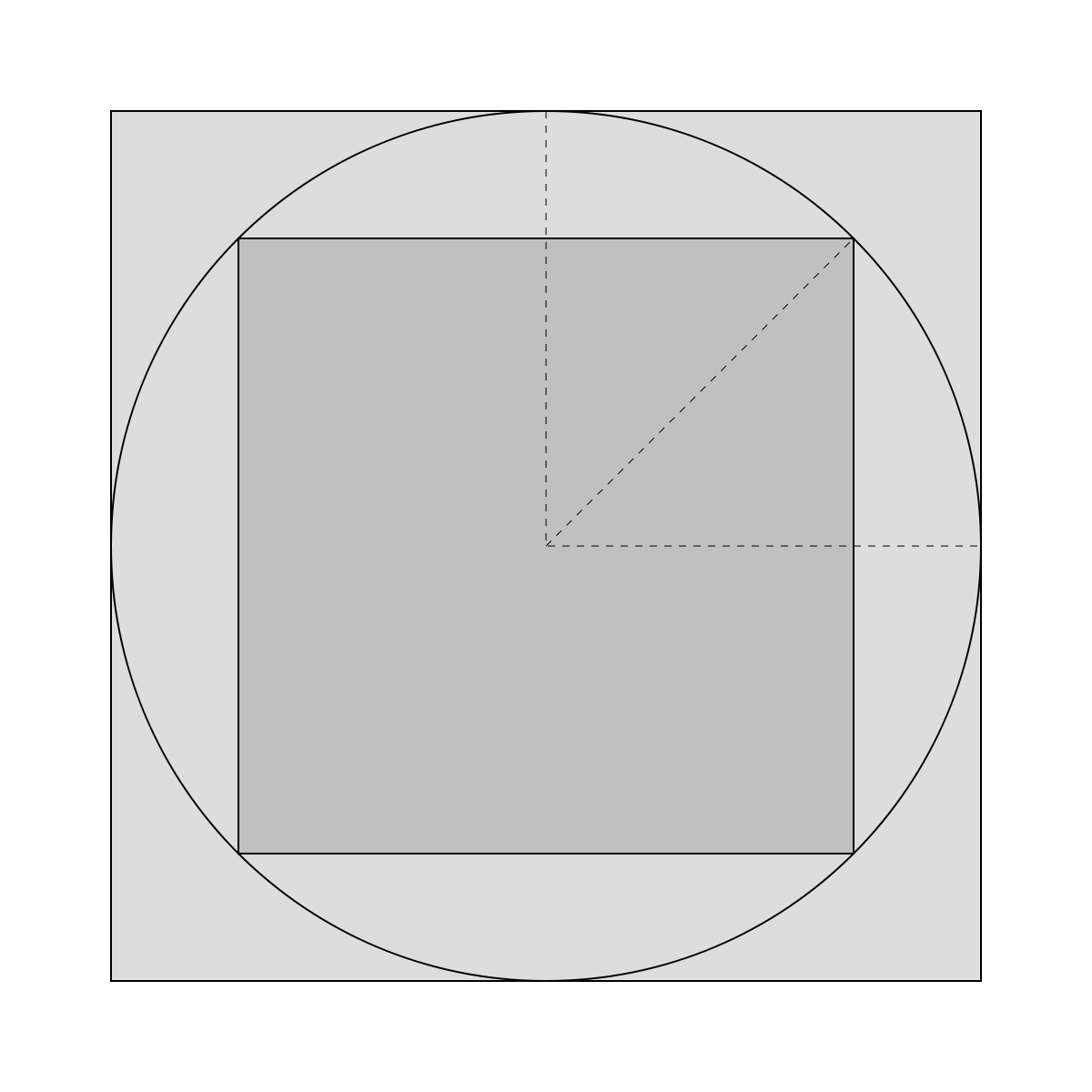
L'aire d'un carré s'obtient par multiplication de la longueur du côté par lui-même. La longueur du côté du carré d'aire 2 multiplié par lui même est donc égal à 2. Par définition de √2, ce carré est de longueur √2.

Il est en outre possible, à l'aide d'un cercle, de dupliquer le carré sans en changer l'orientation. Dans la figure ci-contre le grand carré a une surface double du petit carré. Il suffit pour s'en convaincre de faire pivoter le petit carré d'un huitième de tour. Le rapport des côtés des deux carrés est donc de √2. La figure de gauche illustrera, pour les mathématiciens futurs la présence de la racine carré de deux dans le sinus et le cosinus du huitième de tour.

cos(45°)=sin(45°)=1/√2=√2/2

Plus tard, ce tracé séduit de nombreux architectes comme Andrea Palladio dans sa Villa Rotonda ou dans l’Église ronde de Preslav. On la retrouve dans le cloître de la cathédrale de Cahors où la surface de la cour intérieure est égale à la surface de la galerie qui l'entoure ou dans les carnets de Villard de Honnecourt.

Rendre carré un rectangle

première étape du calcul

Les Babyloniens disposent de puissantes méthodes de calcul et, comme en témoigne la tablette YBC 7289, savent fournir une excellente approximation de √2. Si leur méthode reste encore inconnue, on imagine qu'ils utilisent le raisonnement présenté ici ou un équivalent.

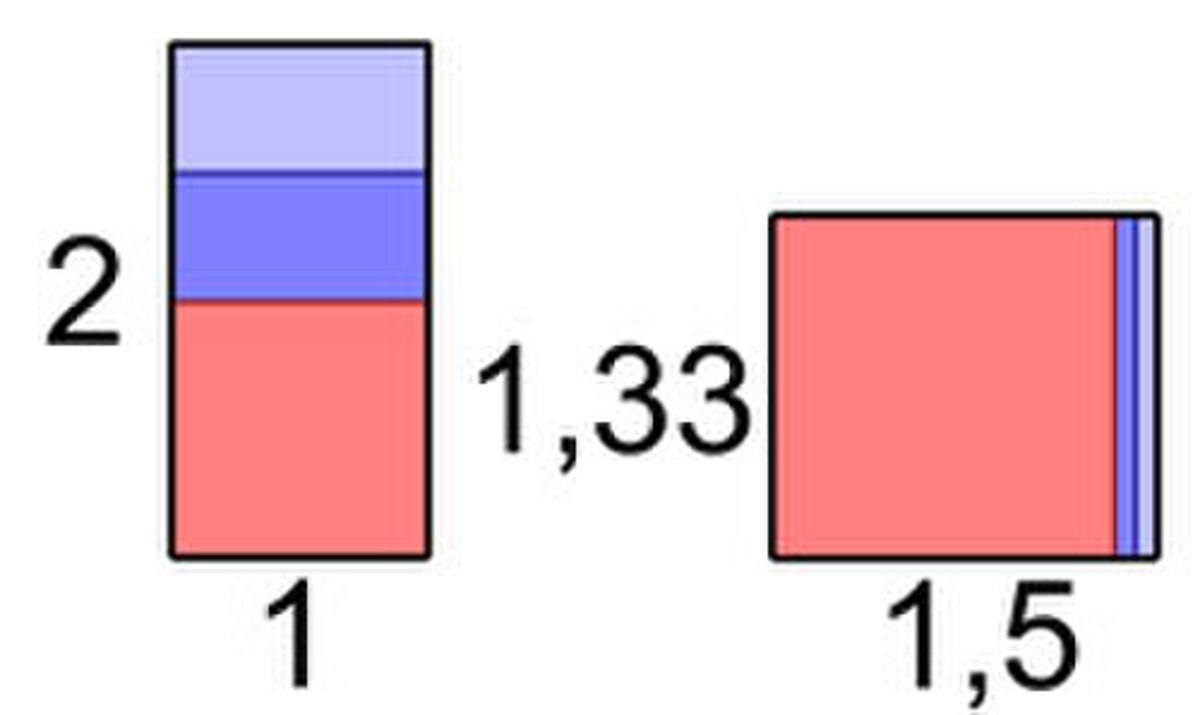
La méthode consiste à construire un carré de la même aire qu'un rectangle. On commence par un rectangle de base 1 et de hauteur 2. Ensuite, pour rendre plus carré ce rectangle, on en construit un deuxième de base la moyenne des longueurs des côtés du premier rectangle, soit 1,5 : la moyenne de 1 et de 2. Sa hauteur est calculée pour que le nouveau rectangle soit d'aire 2, elle vaut 2/1,5 = 1,3333... A l'image des Babyloniens, les calculs sont ici réalisés en numération positionnelle, à l'image de notre notation décimale, mais eux comptent en base 60, ce que l'on ne fait pas ici pour des raisons de simplicité. Si l'on recommence, on trouve pour base la moyenne de 1,5 et de 1,3333... soit 1,4166... et pour hauteur 2/1,416... soit 1,4117... . L'itération suivante donne 1,4142... une approximation avec cinq chiffres significatifs. Pour obtenir la précision babylonienne, il faudrait itérer encore une fois l'opération.

Cette méthode ne donne jamais exactement la bonne valeur, et la suite des chiffres après la virgule ne s'arrête jamais. Pour les Babyloniens, ces difficultés ne sont pas nouvelles, on les trouve aussi pour certaines divisions. Avec les conventions modernes ce phénomène se produit pour 1/3 qui est un nombre proche de 0,3333, mais notre système décimal ne donne jamais exactement la bonne valeur.

Calculer avec √2

Un calcul avec √2

Les Babyloniens savent résoudre des questions du second degré. Cela les amène à pouvoir calculer des expressions contenant la valeur de √2. Pour les Babyloniens, le calcul de (√2 + 1)(√2 - 1), s'exprime comme la multiplication de 2,4142 par 0,4142. Ils ne disposent en effet d'aucun langage symbolique pour écrire √2 et la différence entre les deux expressions est suffisamment petite pour être acceptable.

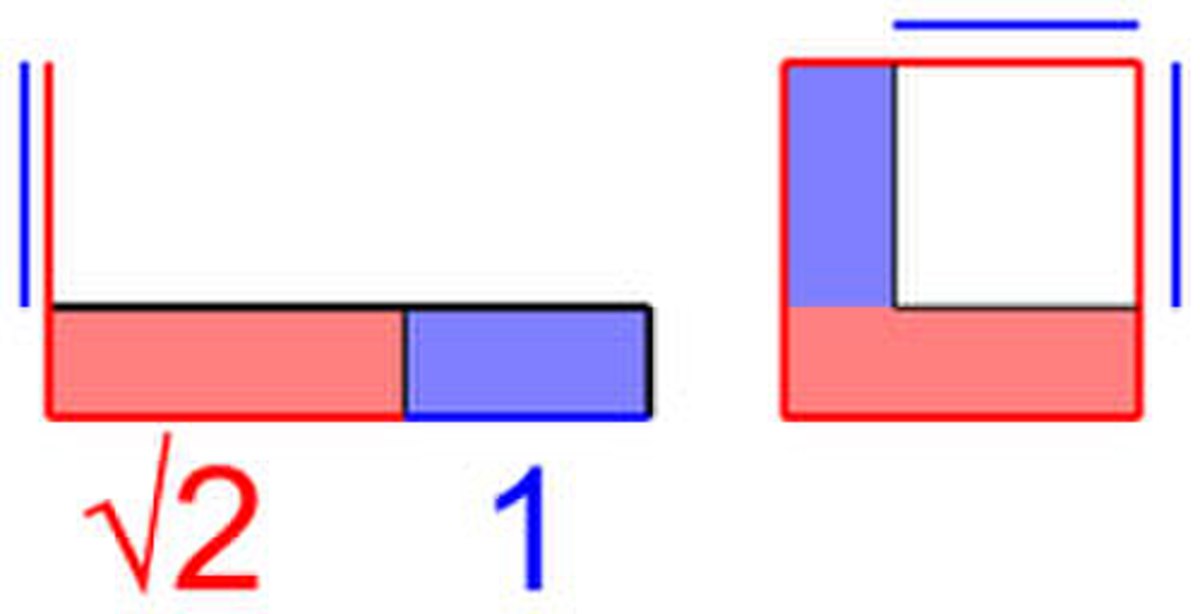
Plutôt que de calculer une multiplication longue et fastidieuse, surtout en base 60, ils raisonnent géométriquement. La question revient à mesurer l'aire d'un rectangle de base √2 + 1 et de hauteur √2 - 1, à l'image de la figure de droite. En déplaçant la zone bleue du rectangle habilement, on remarque que le résultat est la différence entre l'aire d'un carré de côté √2 et l'aire d'un carré de côté 1. Le résultat est donc 1, obtenu en évitant des calculs rébarbatifs. Cette démarche géométrique est l'équivalent des calculs algébriques suivants, si p désigne la longueur de la diagonale d'un carré et q celle de son côté :

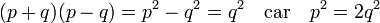
Les Babyloniens utilisent encore d'autres méthodes de calculs, repris et interprétés différemment par les Grecs. Ils ne concernent néanmoins pas directement la racine de deux.

Les calculs chez les babyloniens sont plus complexes que maintenant. Pour réaliser une multiplication en base 10, il suffit de connaître les tables de multiplications jusqu'à 10. L'équivalent chez les babyloniens suppose la connaissance des tables jusqu'à 60. A lieu d'imposer aux apprentis scribes de connaître par cœur des résultats comme 47 x 59, ils utilisaient des méthodes, fondées sur les carrés parfaits.

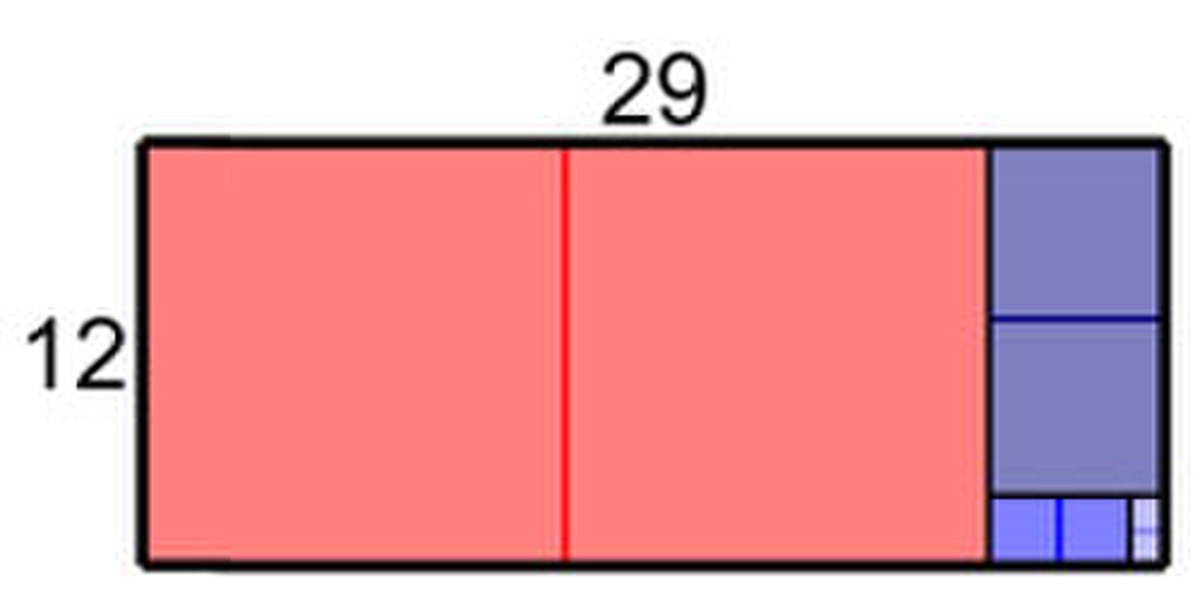
Les babyloniens disposent de tables des carrés, ils s'en servent pour effectuer des multiplications. Illustrons le pour la multiplication de 12 par 29. On remarque que 29 est égal à 2 x 12 + 5. Autrement dit :

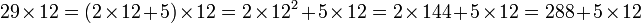
Graphiquement, cela revient à calculer l'aire en rouge sur le rectangle de droite. De la même manière 12 est égal à 2 x 5  2. La prise en compte de la zone bleue foncée donne :

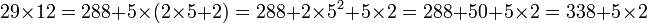
Il est possible de prolonger encore la méthode, mais les babyloniens savaient que 5 x 2 = 10 et le résultat est donc 348.