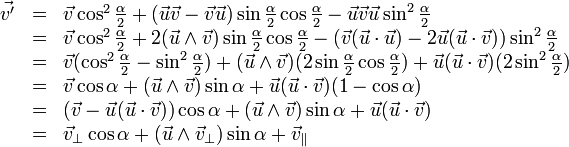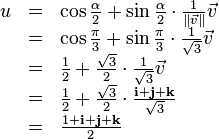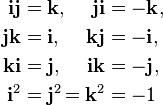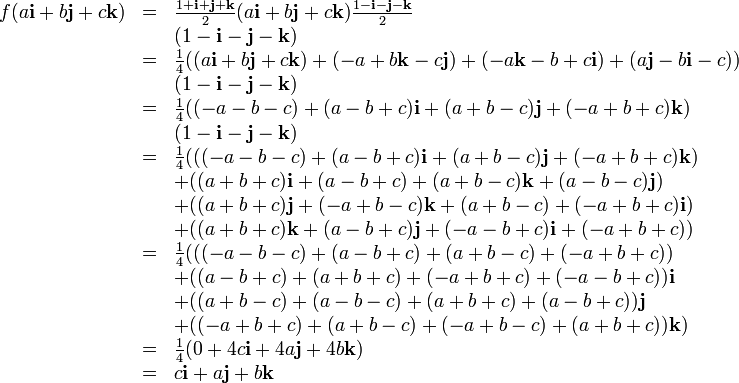Quaternions et rotation dans l'espace - Définition

Introduction

Les quaternions unitaires fournissent une notation mathématique commode pour représenter l'orientation et la rotation d'objets en trois dimensions. Comparés aux angles d'Euler, ils sont plus simple à composer et évitent le problème du blocage de cardan. Comparés aux matrices de rotations, ils sont plus stables numériquement et peuvent se révéler plus efficaces. Les quaternions ont été adoptés dans des applications en infographie, robotique, navigation, dynamique moléculaire et la mécanique spatiale des satellites.

Opérations de rotation à l'aide des quaternions

Une explication très stricte des propriétés utilisées dans cette section est donnée par Altmann.

L'hypersphère des rotations

Se faire une idée de l'espace des rotations

Les quaternions unitaires représentent l'espace mathématique des rotations en trois dimensions de façon relativement simple. On peut comprendre la correspondance entre les rotations et les quaternions en commençant d'abord par se faire une idée intuitive de l'espace des rotations lui-même.

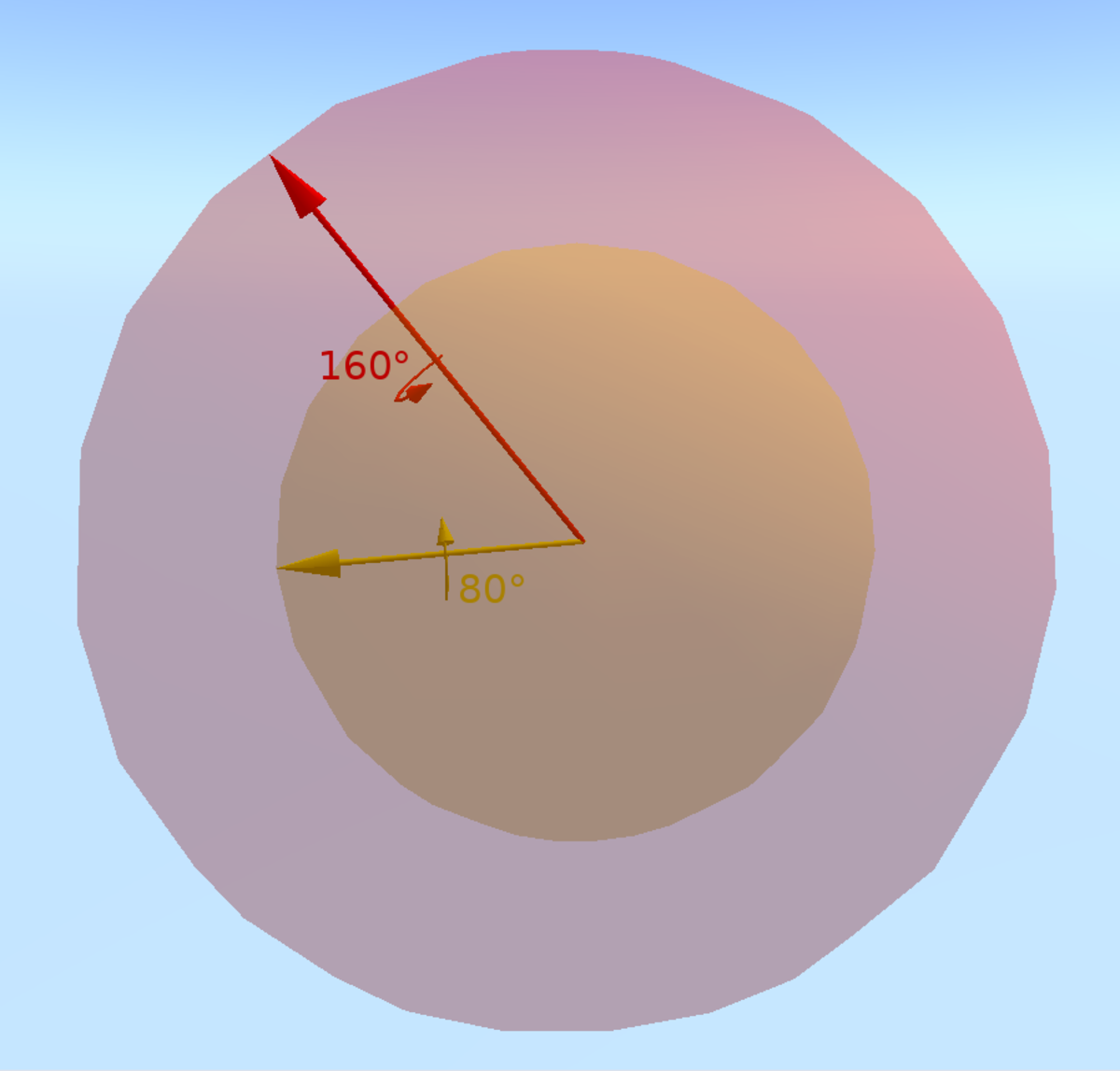
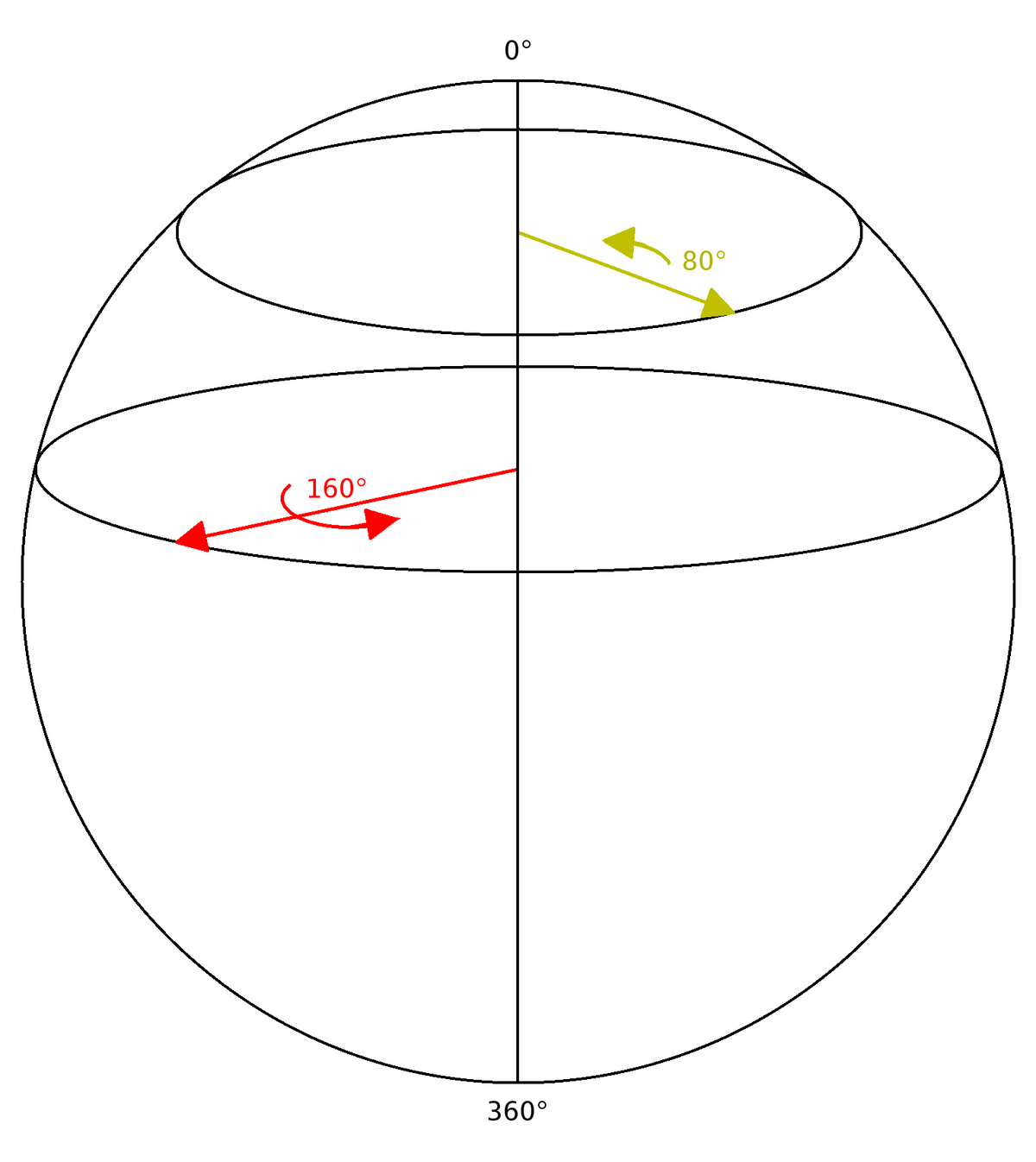
Chaque rotation en trois dimensions consiste à tourner d'un certain angle autour d'un certain axe. Quand l'angle est nul, l'axe n'a pas d'importance, de telle façon qu'une rotation de zéro degrés est un simple point dans l'espace des rotations (c'est la rotation identité). Pour un angle petit mais non-nul, l'ensemble des rotations possibles est une petite sphère entourant la rotation identité, où chaque point de la sphère représente un axe pointant dans une direction particulière (comparez avec la sphère céleste). Des rotations d'angles de plus en plus grands s'éloignent progressivement de la rotation identité, et nous pouvons nous les représenter comme des sphères concentriques de rayons croissants. Par conséquent, au voisinage de la rotation identité, l'espace abstrait des rotations ressemble à l'espace ordinaire en trois dimensions (qui peut également être vu comme un point central entouré de sphères de différents rayons. La ressemblance s'arrête là : lorsque l'angle de rotation dépasse 180°, les rotations suivant les différents axes cessent de diverger et commencent à nouveau à se ressembler, pour finir par devenir identiques (et égales à la rotation identité) lorsque l'angle atteint 360°.

On constate un phénomène analogue à la surface d'une sphère. Si nous nous plaçons au pôle Nord et traçons à partir de là des lignes droites (en fait, des méridiens) dans plusieurs directions, elles divergeront puis convergeront à nouveau au pôle Sud. Des cercles concentriques de rayon croissant dessinés autour du pôle Nord (des parallèles) finiront par s'effondrer en un point au pôle Sud une fois que l'on a parcouru la distance entre les pôles. On peut assimiler les différentes directions à partir du pôle (c'est-à-dire les différents méridiens) aux différents axes de rotations et les différentes distances au pôle Nord aux différents angles : on a ainsi une analogie de l'espace des rotations. Mais la surface de la sphère est en deux dimensions alors que les axes de rotation utilisent déjà trois dimensions. L'espace des rotations est donc modélisé par une hypersphère, c'est-à-dire par une sphère en 4 dimensions. Nous pouvons penser à la sphère ordinaire comme à une section de l'hypersphère, de la même façon qu'un cercle est une section de sphère. On peut prendre la section pour représenter, par exemple, uniquement les rotations d'axes dans le plan xy (voir illustration ci-contre). On remarque que l'angle de la rotation est deux fois la différence de latitude avec le pôle Nord : en effet, les points de l'équateur représentent des rotations de 180°, pas de 90°, et le pôle Sud représente la rotation identité de 360°, et pas le demi-tour de 180°.

Le pôle Nord et le pôle Sud représentent la même rotation, et en fait cela s'applique à n'importe quelle paire de points aux antipodes l'un de l'autre : si un point correspond à une rotation d'angle α autour de l'axe dirigé par le vecteur , l'autre point correspond à une rotation d'angle autour de l'axe dirigé par le vecteur . En fait, l'espace des rotations n'est pas l'hypersphère elle-même, mais l'hypersphère où l'on identifie les points aux antipodes l'un de l'autre. Mais dans un but de simplification, nous pouvons penser aux rotations comme à des points de la sphère en 4 dimensions, même si leur moitié est redondante (revêtement double).

Paramétrer l'espace des rotations

Nous pouvons paramétrer la surface d'une sphère à l'aide de deux coordonnées, comme la latitude et la longitude. Mais la latitude et la longitude se comportent mal (sont dégénérés) aux pôles Nord et Sud, alors que les pôles ne sont pas différents par nature des autres points de la sphère. Aux pôles Nord et Sud (de latitudes +90° et -90°), la longitude perd son sens.

On peut montrer qu'aucun système de coordonnées à deux paramètres ne peut éviter cette dégénérescence (c'est le théorème de la boule chevelue). Nous pouvons éviter de tels problèmes en plongeant la sphère dans l'espace à trois dimensions et en la paramétrant au moyen de trois coordonnées cartésiennes (ici w, x et y), en plaçant le pôle Nord à (w, x, y) = (1, 0, 0), le pôle Sud à (w, x, y) = (−1, 0, 0) et l'équateur sera le cercle d'équations w = 0 et x² + y² = 1. Les points de la sphère satisfont la contrainte w² + x² + y² = 1, donc nous avons toujours deux degrés de liberté, bien que l'on ait trois coordonnées. Un point (w, x, y) de la sphère représente une rotation de l'espace ordinaire autour de l'axe horizontal dirigé par le vecteur 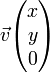et d'angle .

De la même façon, l'hypersphère décrivant l'espace des rotations dans l'espace en trois dimensions peut être paramétrée au moyen de trois angles (angles d'Euler), mais tout paramétrage de ce type dégénère en certains points de l'hypersphère, ce qui conduit au problème du blocage de cardan. Nous pouvons éviter cela en utilisant quatre coordonnées euclidennes w, x, y et z, avec w² + x² + y² + z² = 1. Le point de coordonnées (w, x, y, z) représente une rotation autour de l'axe dirigé par le vecteur 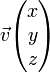et d'angle

Des rotations aux quaternions

Les quaternions en bref

On peut définir les nombres complexes en introduisant un symbole abstrait i qui se conforme aux règles usuelles de l'algèbre et qui en plus obéit à la règle i² = −1. Cela suffit à reproduire toutes les règles de calcul des nombres complexes, par exemple .

De la même façon, les quaternions peuvent être définis en introduisant des symboles abstraits i, j et k qui satisfont aux règles i² = j² = k² = ijk = −1 et les règles algébriques usuelles sauf la commutativité de la multiplication (un exemple familier de multiplication non commutative est la multiplication des matrices). L'ensemble des règles de calcul découle de ces définitions ; par exemple, on peut montrer que .

La partie imaginaire d'un quaternion se comporte comme un vecteur 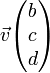d'un espace vectoriel à trois dimensions et la partie réelle a comme un scalaire de . Quand les quaternions sont utilisés en géométrie, il est pratique de les définir comme un scalaire plus un vecteur: .

Ceux qui ont étudié les vecteurs à l'école pourront trouver étrange d'additionner un nombre à un vecteur, car ce sont des objets de natures très différentes, ou de multiplier deux vecteurs entre eux, car cette opération n'est d'habitude pas définie. Néanmoins, si l'on se souvient qu'il ne s'agit là que d'une notation pour les parties réelles et imaginaires d'un quaternion, cela devient plus légitime.

Nous pouvons exprimer la multiplication de quaternions dans le langage moderne du produit vectoriel et du produit scalaire de vecteurs (qui ont en fait été inspirés au début par les quaternions). À la place des règles i² = j² = k² = ijk = −1, nous avons la règle de multiplication de deux vecteurs , où :

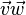• est la multiplication de vecteurs,
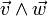• est le produit vectoriel (un vecteur),
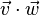• est le produit scalaire (un nombre).

La multiplication de vecteurs n'est pas commutative (à cause du produit vectoriel), alors que la multiplication entre scalaires et entre un scalaire et un vecteur sont commutatives. Il découle de manière immédiate de ces règles que .

L'inverse (à gauche et à droite) d'un quaternion non nul est , comme cela peut être vérifié par calcul direct.

Relation entre les rotations et les quaternions

Soient (w, x, y, z) les coordonnées d'une rotation, comme décrit précédemment. Définissons le quaternion : 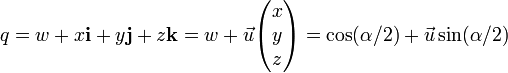où est un vecteur unitaire. Soit également un vecteur ordinaire de l'espace en 3 dimensions, considéré comme un quaternion avec une coordonnée réelle nulle. On peut alors montrer (voir section suivante) que le produit de quaternions

renvoie le vecteur tourné d'un angle α autour de l'axe dirigé par . La rotation se fait dans le sens des aiguilles d'une montre si notre ligne de vue pointe dans la même direction que . Cette opération est connue comme la conjugaison par q.

Il s'ensuit que la multiplication de quaternions correspond à la composition de rotations, car si p et q sont des quaternions representant des rotations, alors la rotation (conjugaison) par pq est

,

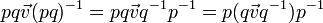ce qui revient à tourner (conjuguer) par q, puis par p.

Le quaternion inverse d'une rotation correspond à la rotation inverse, car . Le carré d'un quaternion correspond à la rotation de deux fois le même angle autour du même axe. Plus généralement, qⁿ correspond à une rotation de n fois l'angle autour du même axe que q. Cela peut être étendu à un réel arbitraire n, ce qui permet d'e calculer des rotations intermédiaires de façon fluide entre des rotation de l'espace, c'est l'interpolation linéaire sphérique (Slerp).

Démonstration de l'équivalence entre conjugaison de quaternions et rotation de l'espace

Soit un vecteur unitaire (l'axe de rotation) et soit . Notre but est de montrer que

renvoie le vecteur tourné d'un angle α autour de l'axe dirigé par . En développant, on obtient

où et sont les composantes de respectivement orthogonale et colinéaire à . C'est là la formule de Olinde Rodrigues qui donne la rotation d'angle α autour de l'axe dirigé par .

Exemple

L'action par conjugaison

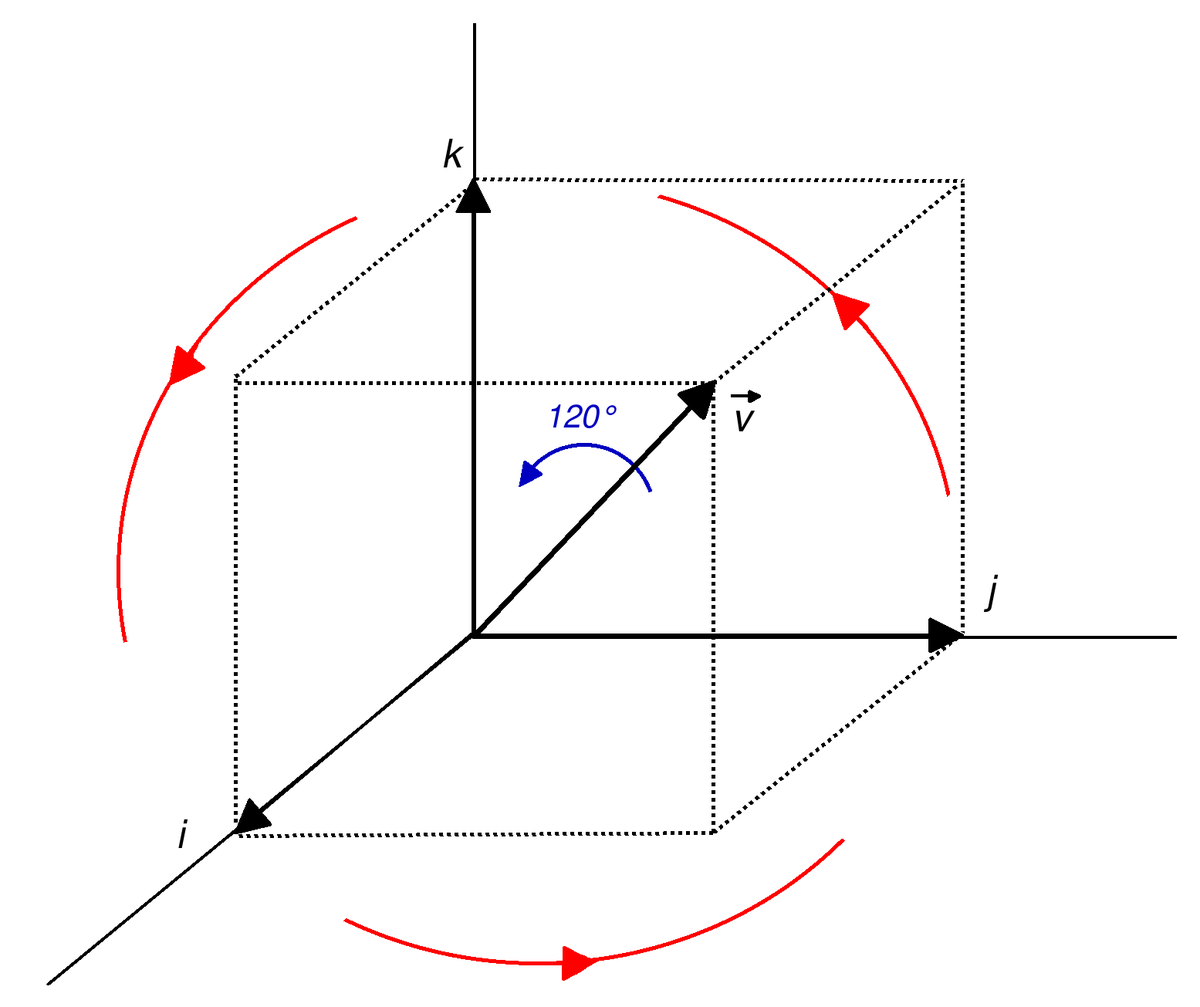
Considérons la rotation f autour de l'axe dirigé par et d'angle 120°, c'est-à-dire ^2π/₃ radians.

La norme de est √3, le demi-angle est ^π/₃ (60°), le cosinus de ce demi-angle est ¹/₂, (cos 60° = 0,5) et son sinus est ^√3/₂, (sin 60° ≈ 0,866). Nous devons donc conjuguer avec le quaternion unitaire :

Si f est la fonction de rotation,

On peut prouver que l'on obtient l'inverse d'un quaternion unitaire simplement en changeant le signe de ses coordonnées imaginaires. En conséquence,

et

En appliquant les règles ordinaires de calcul avec les quaternions, on obtient

Comme on s'y attendait, la rotation revient à tenir un cube par un de ses sommets, puis à le faire tourner de 120° selon la diagonale la plus longue qui passe par ce point. On observe comme les trois axes subissent une permutation circulaire.

Les calculs de quaternions en pratique

Prouvons le résultat précédent. En développant l'expression de f (en deux étapes) et en appliquant les règles :

on obtient :

ce qui est bien le résultat annoncé. On voit que de tels calculs sont relativement fastidieux à faire à la main, mais dans un programme d'ordinateur, cela se résume à appeler deux fois la routine de multiplication de quaternions.