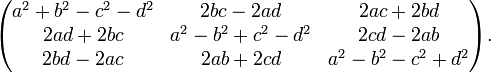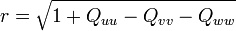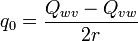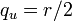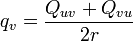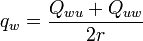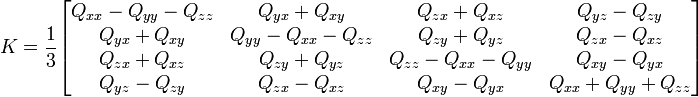Quaternions et rotation dans l'espace - Définition

Les quaternions et les autres représentations des rotations

Description qualitative des avantages des quaternions

La représentation d'une rotation sous la forme d'un quaternion (4 nombres) est plus compacte que la représentation en tant que matrice orthogonale (9 nombres). De plus, pour un axe et un angle donné, on peut facilement construire le quaternion correspondant, et réciproquement, pour un quaternion donné, on peut facilement extraire l'axe et l'angle. Toutes ces opérations sont beaucoup plus difficiles avec des matrices ou des angles d'Euler.

Dans les jeux vidéo et dans d'autres applications, on a souvent besoin de « rotations fluides », c'est-à-dire que la scène représentée doit tourner harmonieusement et pas d'un seul coup. On peut obtenir ce résultat en choisissant une courbe comme celle de l'interpolation linéaire sphérique dans l'espace des quaternions, avec une extrémité qui est la transformation identique 1 (ou correspondant à une autre rotation initiale) et l'autre extrémité correspondant à la rotation finale désirée. C'est plus difficile à faire avec d'autres représentations des rotations.

Quand on compose plusieurs rotations sur un ordinateur, les erreurs d'arrondi s'accumulent forcément. Un quaternion qui est légèrement erroné représente toujours une rotation après avoir été renormalisé ; une matrice qui est légèrement erronée ne sera plus orthogonale et est dure à convertir à nouveau en une matrice orthogonale qui convienne.

Les quaternions évitent également un phénomène appelé le blocage de cardan qui peut apparaître lorsque, par exemple dans des systèmes de rotations décrivant le roulis, le tangage et le lacet, le tangage est de 90° vers le haut ou le bas, de telle façon que le roulis et le lacet correspondent au même mouvement, et qu'un degré de liberté ait été perdu. Dans un système de navigation inertielle à base de cardans, par exemple, cela peut avoir des conséquences désastreuses si l'avion monte en flèche ou descend à pic.

Conversion vers et depuis la représentation sous forme de matrice

D'un quaternion en matrice orthogonale

La matrice orthogonale correspondant à une rotation au moyen du quaternion unitaire z = a + bi + cj + dk (avec |z| = 1) est donnée par

D'une matrice orthogonale en quaternion

Chercher le quaternion (q₀ + q_xi + q_yj + q_zk) correspondant à la matrice de rotation Q_ij peut être instable numériquement si la trace (la somme des éléments de la diagonale de la matrice) de la matrice de rotation est nulle ou très petite. Une méthode robuste consiste à choisir l'élément de la diagonale ayant la valeur Q_uu la plus grande en valeur absolue. Considérons

où uvw est une permutation paire de xyz (c'est-à-dire xyz, yzx ou zxy). Cette écriture est légitime car l'expression sous la racine est positive. Le quaternion peut alors être écrit sous la forme :

Attention, il y a deux conventions pour les vecteurs : l'une suppose que les matrices de rotation sont multipliées par des vecteurs-ligne à gauche, l'autre par des vecteurs-colonne à droite ; les deux conventions conduisent à des matrices qui sont transposées l'une de l'autre. La matrice ci-dessus suppose que l'on utilise des vecteurs colonne à droite. Historiquement, la convention vecteur-colonne-à-droite provient des mathématiques et de la mécanique classique, alors que la convention vecteur-ligne-à-gauche provient de l'infographie, où il était plus facile de saisir des vecteurs-lignes aux débuts de la discipline.

Quaternions optimaux

La section ci-dessus a décrit comment récupérer un quaternion q à partir d'une matrice de rotation 3 × 3 Q. Supposons, néanmoins, que nous avons une matrice Q qui n'est pas celle d'une rotation pure, à cause d'erreurs d'arrondi, par exemple, et que nous souhaitions trouver le quaternion q qui représente Q le plus précisément possible. Dans ce cas, nous construisons une matrice 4 × 4 symétrique

et nous cherchons le vecteur propre de coordonnées (x, y, z, w) correspondant à la plus grande valeur propre (cette valeur vaut 1 si et seulement si Q est une rotation pure). Le quaternion ainsi obtenu correspondra à la rotation la plus proche de la matrice Q de départ.

Comparaisons de performances avec d'autres méthodes de rotation

Cette section traite des implications en termes de performances de l'utilisation de quaternions par rapport à d'autres méthodes (axe et angle ou matrices de rotation) pour effectuer des rotations en 3D.

Résultats

Espace mémoire nécessaire

Méthode	Mémoire
Matrice de rotation	9
Quaternion	4
Axe et angle	4*

* Note : la réprésentation sous forme d'angle et d'axe peut être stockée dans 3 emplacements seulement en multipliant l'axe de rotation par l'angle de rotation ; néanmoins, avant de l'utiliser, il faut récupérer le vecteur unitaire et l'angle en renormalisant, ce qui coûte des opérations mathématiques supplémentaires.

Comparaison de performances de la composition de rotations

Méthode	Multiplications	Additions et soustractions	Nombre total d'opérations
Matrices de rotation	27	18	45
Quaternions	16	12	28

Comparaison de performances de la rotation de vecteurs

Méthode	Multiplications	Additions et soustractions	sin et cos	Nombre total d'opérations
Matrice de rotation	9	6	0	15
Quaternions	21	18	0	39
Axe et angle	23	16	2	41

Méthodes utilisées

Il y a trois techniques de base pour faire tourner un vecteur  :

1. Calculer le produit matriciel de la matrice de rotation 3x3 représentant la rotation R par la matrice colonne 3x1 représentant le vecteur . Cela nécessite 3 x (3 multiplications + 2 additions) = 9 multiplications at 6 additions, c'est la méthode la plus efficace pour faire tourner un vecteur.
2. Utiliser la formule de rotation avec des quaternions dite . Calculer ce résultat revient à transformer le quaternion en une matrice de rotation R en utilisant la formule de conversion , puis à multiplier le résultat par la matrice-colonne représentant le vecteur. En procédant à une recherche de sous-expressions communes, l'algorithme se ramène à 21 multiplications et 18 additions. Une autre approche peut consister à convertir d'abord le quaternion dans la représentation sous forme d'axe et d'angle équivalente, puis à s'en servir pour faire tourner le vecteur. Néanmoins, c'est à la fois moins efficace et moins stable numériquement lorsque le quaternion est voisin de la rotation identité.
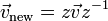
3. Convertir la représentation sous forme d'axe et d'angle en matrice de rotation R, puis multiplier par la matrice-colonne représentant le vecteur. La conversion coûte 14 multiplications, 2 appels de fonction (sin et cos) et 10 additions ou soustractions après recherche de sous-expressions communes, puis la rotation ajoute 9 multiplications et 6 additions pour un total de 23 multiplications, 16 additions ou soustractions et deux appels de fonctions trigonométriques.

Pseudo-code pour la rotation à l'aide de quaternions

Étant donné un quaternion z = a + bi + cj + dk (avec |z| = 1) et un vecteur de coordonnées v1, v2 et v3, le code qui suit effectue une rotation. Notez l'utilisation de variables temporaires txx. Notez aussi l'optimisation des éléments de la diagonale de la matrice R : comme a² + b² + c² + d² = 1, on réécrit l'élément en haut à gauche sous la forme a² + b² + c² + d² − 2c² − 2d² = 1 − 2c² − 2d² ; les deux autres éléments de la diagonale peuvent être réécrits de même.

      t2 =   a*b      t3 =   a*c      t4 =   a*d      t5 =  -b*b      t6 =   b*c      t7 =   b*d      t8 =  -c*c      t9 =   c*d      t10 = -d*d      v1new = 2*( (t8 + t10)*v1 + (t6 -  t4)*v2 + (t3 + t7)*v3 ) + v1      v2new = 2*( (t4 +  t6)*v1 + (t5 + t10)*v2 + (t9 - t2)*v3 ) + v2      v3new = 2*( (t7 -  t3)*v1 + (t2 +  t9)*v2 + (t5 + t8)*v3 ) + v3      

Pseudo-code pour créer une matrice angle et axe

Étant donnés un vecteur unitaire de coordonnées (v1, v2, v3) et un angle θ, la matrice de rotation peut être calculée avec :

      t1 =  cos(theta)      t2 =  1 - t1      t3 =  v1*v1      t6 =  t2*v1      t7 =  t6*v2      t8 =  sin(theta)      t9 =  t8*v3      t11 = t6*v3      t12 = t8*v2      t15 = v2*v2      t19 = t2*v2*v3      t20 = t8*v1      t24 = v3*v3      R[1, 1] = t1 + t2*t3      R[1, 2] = t7 - t9      R[1, 3] = t11 + t12      R[2, 1] = t7 + t9      R[2, 2] = t1 + t2*t15      R[2, 3] = t19 - t20      R[3, 1] = t11 - t12      R[3, 2] = t19 + t20      R[3, 3] = t1 + t2*t24