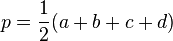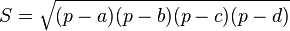Quadrilatère - Définition

Caractéristiques

Un quadrilatère est la figure notée « ABCD » formée par :

• quatre points A, B, C et D : les sommets du quadrilatère ;
• quatre segments [AB], [BC], [CD] et [DA] : les côtés du quadrilatère.

Les sommets A et C sont dits opposés ; ainsi que les sommets B et D.
Les diagonales [AC] et [BD] joignent les sommets opposés.

Un quadrilatère peut être :

• convexe, si les deux diagonales sont à l'intérieur du quadrilatère ;
• concave, si (au moins) une des diagonales est à l'extérieur du quadrilatère ;
• croisé, si les deux diagonales sont à l'extérieur du quadrilatère. Un quadrilatère croisé est concave.

Typologie des quadrilatères

Les quadrilatères quelconques offrent relativement peu d'intérêt, mais permettent de voir ce qui se cache derrière les définitions des quadrilatères particuliers bien connus ( trapèze, parallélogramme, rectangle, losange, carré, Cerf-volant, Pseudo-carré... )

Quand on cherche à classer les quadrilatères en leur imposant des propriétés particulières, on obtient par exemple :

Diagonales perpendiculaires

Cette catégorie ne présente pas de régularité d'aspect. Parmi les quadrilatères convexes dont les diagonales sont perpendiculaires, on peut noter

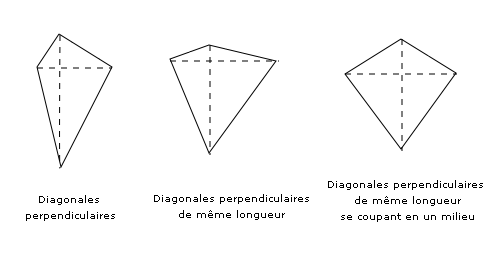
• Les quadrilatères dont les diagonales sont perpendiculaires et deux côtés consécutifs égaux : le cerf-volant, le losange , le cerf-volant concave dit « pointe de flèche ».
• Un quadrilatère dont les diagonales sont perpendiculaires et de même longueur : le pseudo-carré.

L'aire de tous ces quadrilatères convexes est (où D et d sont les mesures des diagonales).

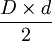
Côtés égaux deux à deux

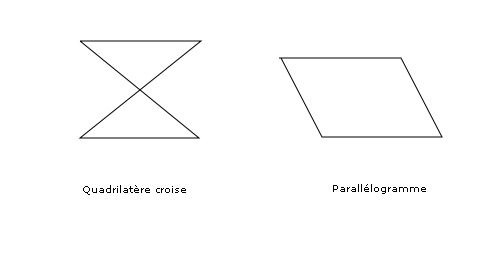
On n'obtient pas toujours un parallélogramme. Pour obtenir un parallélogramme, il faut que le quadrilatère soit en outre convexe et que les côtés opposés soient égaux . Si le quadrilatère n'est pas convexe et les côtés opposés sont égaux deux à deux, on obtient un quadrilatère croisé : l'antiparallélogramme.

Si les côtés égaux sont consécutifs deux à deux, on retombe sur le cerf-volant pour un quadrilatère convexe et la flèche pour un quadrilatère concave

Côtés parallèles

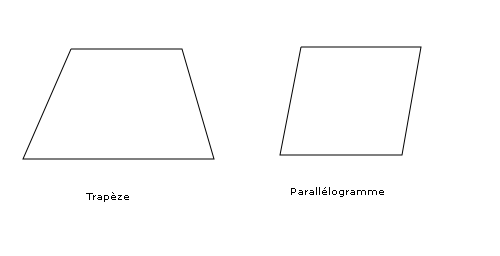
On retrouve là deux classes intéressantes de quadrilatères convexes : les trapèzes et les parallélogrammes.

Parmi les trapèzes particuliers, on trouve le trapèze isocèle dont les côtés non parallèles sont de même longueur et le trapèze rectangle qui possède deux angles droit.

Parmi les parallélogrammes particuliers on trouve les rectangles (parallélogrammes à angles droits), les losanges (parallélogrammes à côtés adjacents égaux) et les carrés (à la fois rectangles et losanges).

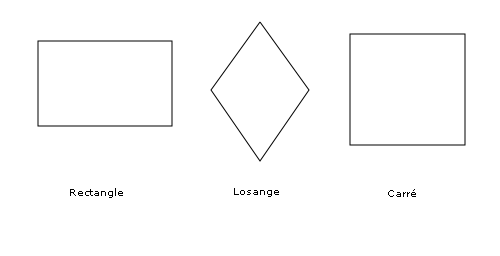
Ainsi, selon cette classification, le carré est le quadrilatère le plus riche en propriétés. Il est aussi l'unique solution du problème isopérimétrique pour les quadrilatères. C'est-à-dire que, parmi tous les quadrilatères de même périmètre, le carré est celui qui possède la plus grande surface.

Quadrilatères inscriptibles

Les quadrilatères inscriptibles dans un cercle sont les quadrialtères dont les sommets sont cocycliques.

Figure du théorème de Ptolémée :
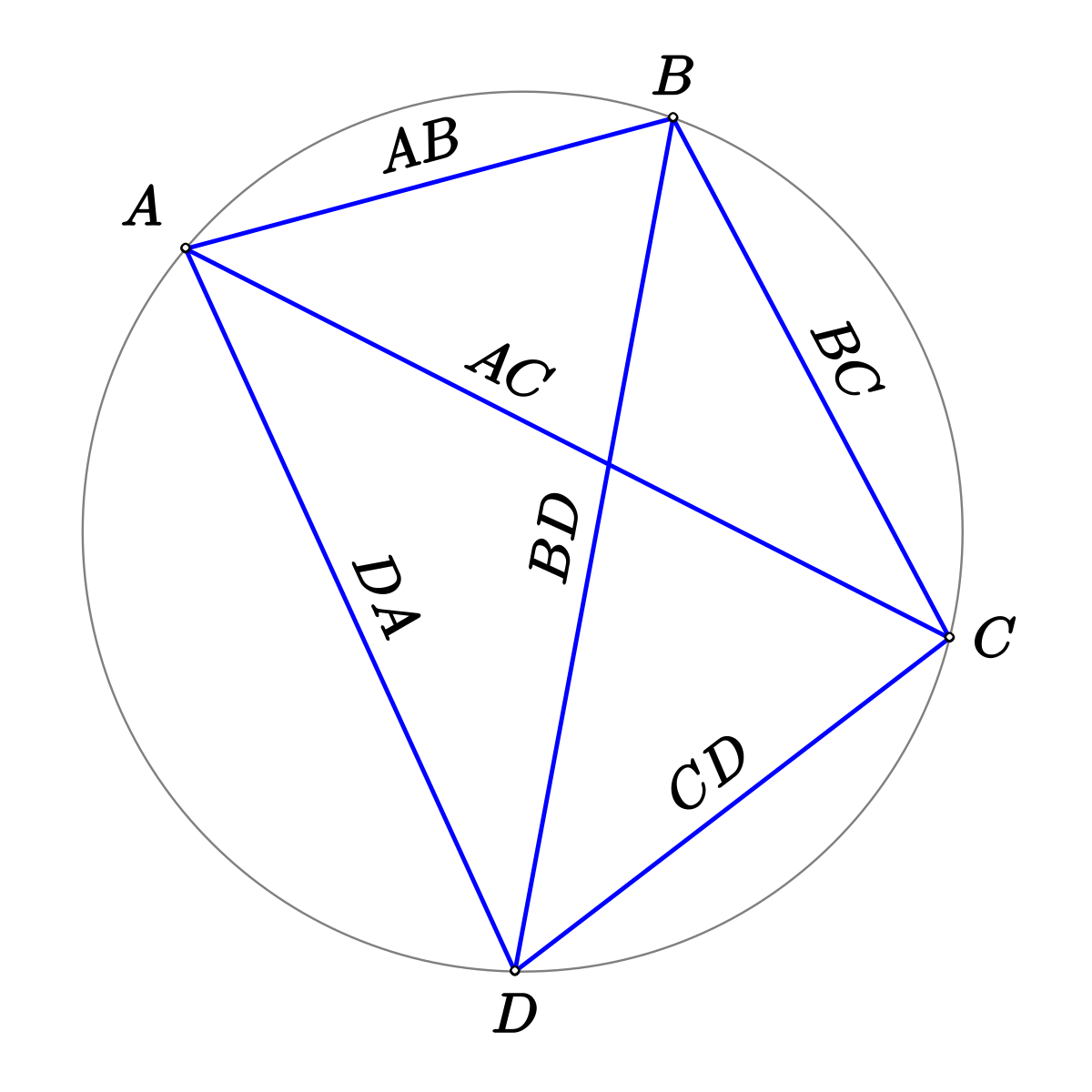
AC × BD= AB.CD+AD.BC

Le théorème de l'angle inscrit permet la caractérisation suivante : un quadrilatère est inscriptible si, et seulement si, il possède deux angles opposés égaux ou supplémentaires : quand les angles sont supplémentaires il s'agit d'un quadrilatère convexe, et quand les angles sont égaux, il s'agit d'un quadrilatère croisé.

En particulier, un trapèze isocèle, un rectangle sont des quadrilatères inscriptibles.

Le théorème de Ptolémée permet d'affirmer qu'un quadrilatère convexe est inscriptible si, et seulement si, le produit des longueurs des diagonales est égal à la somme des produits des longueurs des côtés opposés.

La formule de Brahmagupta donne l'aire d'un quadrilatère convexe dont les sommets se situent sur un même cercle en ne connaissant que la longueur de ses côtés.

où est le demi-périmètre du quadrilatère, a, b, c et d sont les longueurs de ses côtés et S son aire.