Puits de potentiel - Définition

Taux d'harmoniques

L'oscillation n'est pas en général harmonique. Il est usuel de poser :

v²(s) = 2g(H − h(s)): = (s − a(H))²N²(s), et s=a(H).\cosφ. Ainsi :

,

la fonction N(s)(en Hertz) étant généralement bornée : N1 < N < N2, alors T2 < T(H) < T1.

• Le cas du pendule cycloïdal, vu dans le paragraphe précédent, est le plus facile, car N(s)= cste = No , donc T(H)= cste= To.

• Niveau plus élevé : Le cas du pendule simple, beaucoup plus difficile à analyser, est assez banal (on dit générique): si la cuvette présente un sommet arrondi concave, de hauteur H_max, alors usuellement T(H) tend vers l'infini logarithmiquement quand H tend vers H_max. Cet effet de ralentissement est appelé effet Ramsauer en physique nucléaire et a son correspondant en mécanique quantique. Il ressemble beaucoup à l'effet "soliton", analysé dans l'article pendule simple:

soit la décomposition en série de Fourier de s(t) : ,

le taux d'harmoniques est pratiquement non décroissant jusqu'à une valeur , puis s'écroule exponentiellement (donc très vite), dès que n >  : cela est essentiellement dû au caractère indéfiniment dérivable de s(t), c’est-à-dire à la "régularité" de la cuvette (cf Appell, mécanique, 1915).

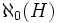
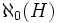
• Note annexe : préciser, néanmoins, qu'il ne faudrait pas croire que l'anharmonicité soit toujours due à ce mécanisme de ralentissement T(H) ; on connaît des cas de cuvettes (non-symétriques) où T(H) = cste = To, mais où l'anharmonicité devient très grande. Dans ce cas, la fonction périodique s(t) ressemble alors à de la houle très pointue. À titre d'exemple V(x) = x -sqrt(x)), étudié en physique des plasmas.

• Enfin, il reste les cas où V(x) présente des singularités : le cas évident est celui d'une particule simplement bloquée entre deux murs réflecteurs : |x|

Alors on a évidemment la vitesse v(x) constante (au signe près), égale à sqrt( 2E/m) et la période T(E) = 2 a/sqrt(2E/m). L'analyse de Fourier de s(t), qui est une fonction "triangle", donne des coefficients qui décroissent comme 1/n^2 et non pas exponentiellement.

• D'autres types de puits de potentiel plus complexes existent [on pensera à (exp-x²).x^10.(x-a)².sin a²/(x-a)², où le nombre de racines de V'(x) augmente indéfiniment quand x tend vers a] :

Ces problèmes à plusieurs "fenêtres de sortie" donneront du mal à être quantifiés en mécanique quantique : c'est le problème des barrières de potentiel double , voire triple en radio-activité.

Fin de note annexe.

Cuvettes non symétriques

Il suffit de remarquer avec Newton que seule importe la section du puits de potentiel V(x) par la droite d'énergie E. On se ramène alors, "à la Cavalieri", à un puits de potentiel symétrique.

Sont de ce type :

• le potentiel (1-2)(dit de Newton radial), -g²/x + h²/x²
• le potentiel harmonique : g² x² +h²/x²
• le potentiel de Lenard-Jones(6-12),
• le potentiel interatomique dans une molécule diatomique, dit de Morse :

U(x) = g²(2exp(x) + exp(-2x) -3 )

• le potentiel nucléaire :

U(x) = g²/sh²x -h²/ch²x

• Remarque : U(x)=-g².x^4 amène la particule à l'infini en un temps fini ; c'est donc assez irréaliste d'avoir de telles forces répulsives.

Remarque : supersymétrie

Les potentiels précités ne sont pas trouvés au hasard ; ils résultent plus ou moins d'une sorte de factorisation, déjà remarquée par Schrodinger en 1940, et puis retrouvée par Ingold et bien d'autres, pour des besoins bien différents.

Évidemment, il se trouve que l'oscillateur harmonique radial et l'atome de Rutherford en font partie.