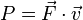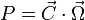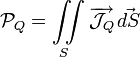Puissance (physique) - Définition

En mécanique

Puissance d'une force

Si le point d'application d'une force (en N) se déplace à la vitesse instantanée (en m/s), alors la puissance instantanée vaut (en W)

On retrouve aisément ce résultat en dérivant le travail d'une force.

Puissance d'un couple.

Si l'objet est en rotation sous l'action d'un couple (en N·m) et tourne à la vitesse de rotation instantanée (en rad/s), alors la puissance instantanée vaut (en W)

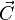
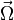
Puissance des interactions.

Dans une liaison parfaite, la puissance des interactions est nulle. On obtient cette grandeur par le calcul du co-moment des torseurs cinématique et statique de la liaison.

Puissance des torseurs

Principe des puissances virtuelles

C'est un principe fondamental en mécanique, il met sous forme variationnelle les équations traditionnelles de la mécanique. Il permet aussi d'établir des relations entre les puissances extérieures d'un mécanisme (et donc d'obtenir des lois entrée/sortie par exemple).

Puissance thermique

La puissance thermique est une notion attachée au flux thermique (ou flux de chaleur) à travers une surface. Cette notion de conduction thermique est expliquée dans les articles Conduction thermique et transfert thermique. Dans ces articles, on introduit de manière unidimensionnelle la densité de flux thermique : .

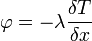
Pour généraliser cette densité de flux dans toutes les directions (y et z), on définit le vecteur densité de flux thermique suivant : (loi de Fourier).

Cette expression de la propagation de chaleur présente 2 avantages :

• elle est tridimensionnelle (elle exprime la propagation dans toutes les directions de l'espace)
• on peut librement utiliser les coordonnées de notre choix (cartésiennes, cylindriques ou sphériques)

Le choix des coordonnées dépend de la symétrie du problème. Par exemple, si on étudie la chaleur produite par un fusible (cylindrique), on utilisera bien sûr les coordonnées cylindriques.

La puissance thermique à travers une surface S (noté ), par définition, est le flux du vecteur à travers la surface S, c'est-à-dire :

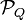
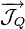
Remarques

• Les systèmes de coordonnées sont détaillés dans l'article suivant : Système de coordonnées
• La surface S peut être ouverte ou fermée. La différence entre une surface fermée et une surface ouverte est expliquée dans l'article : Surface