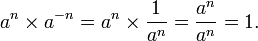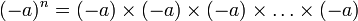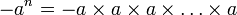Puissance (algèbre) - Définition

Opérations algébriques sur les puissances

Il n'y a pas de formule générale sur les additions ou les soustractions de puissances, sauf la factorisation de aⁿ − bⁿ et le développement de (a + b)ⁿ.

En revanche, pour les multiplications et les divisions de puissances, on sait que pour tous nombres a et b et pour tous entiers naturels m et n non nuls :

•  ;

• si a ≠ 0 ;

• (n’est vrai dans le cas général que si a et b commutent)

•  ;

• si b ≠ 0.

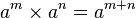
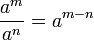
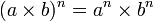
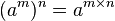
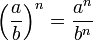
Ces formules sont encore valables si m ou n sont des entiers strictement négatifs, à condition que a et b soient non nuls.

On remarque que la convention « a⁰ = 1 pour tout nombre réel a ≠ 0 » est cohérente avec ces formules ; en effet, pour tout entier naturel n ≠ 0 et pour tout nombre réel a ≠ 0,

• 
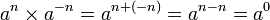
  et

• 

On remarquera qu'en prenant n = 0, les égalités précédentes restent vraies.

Signe de l'exposant et signe du nombre

Il n'y a pas de rapport direct entre le signe de l'exposant et le signe du résultat. Celui-ci dépend de la parité de l'exposant.

Un nombre élevé à une puissance paire donne un résultat positif :

si n est pair, alors ( − a)ⁿ = aⁿ.

Un nombre élevé à une puissance impaire donne un résultat du même signe :

si n est impair, alors ( − a)ⁿ = − aⁿ.

Exemples.

• (-2)³, puissance cubique de -2, vaut (-2) × (-2) × (-2) = -8 < 0.
• 3⁻⁴, l'inverse de la puissance quatrième de 3, vaut

Remarque.

Il ne faut pas confondre les écritures ( − a)ⁿ, où la puissance s'applique à -a (signe moins compris) et − aⁿ, où la puissance s'applique à a uniquement. En effet :

• 
• 

Exponentielle

Les puissances entières sont en fait des cas particuliers de la fonction exponentielle :

a^b = exp(b ln a), définie pour tout réel a > 0.

À partir de la fonction exponentielle, on peut définir :

• des puissances fractionnaires : , où n est un entier, qui coïncident avec les racines n^es pour tout x > 0. Voir racine carrée, racine cubique et racine d'un nombre ;
• des puissances réelles : x^y peut être défini pour y réel et tout x > 0.

Ces puissances fractionnaires et réelles répondent aux même règles que les puissances entières. Notamment, pour tous a > 0, b et c réels quelconques :

•  ;
• .

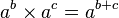
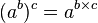
On a en particulier :

• , pour tout entier b ;
• , si c est entier ;
• si b ≠ 0.

Puissances de dix

Les puissances de 10 sont des cas particuliers de puissance. Leur intérêt réside dans le fait que notre écriture est décimale.

Table des puissances de dix

Puissance de dix négatives ou nulle	Préfixe		Puissance de dix positives ou nulle	Préfixe
10⁰ = 1	-		10⁰ = 1	-
10⁻¹ = 0,1	d (déci-)		10¹ = 10	da (déca-)
10⁻² = 0,01	c (centi-)		10² = 100	h (hecto-)
10⁻³ = 0,001	m (milli-)		10³ = 1 000	k (kilo-)
10⁻⁴ = 0,000 1	-		10⁴ = 10 000	-
10⁻⁵ = 0,000 01	-		10⁵ = 100 000	-
10⁻⁶ = 0,000 001	µ (micro-)		10⁶ = 1 000 000	M (méga-)
etc.	etc.		etc.	etc.

Le nombre 10 élevé à une puissance entière positive n est un chiffre 1 suivi de n zéros.

Le nombre 10 élevé à une puissance entière négative -n est un 1 placé à la n ^e position dans un nombre décimal, i. e. précédé de n zéros en comptant celui avant la virgule.

On utilise fréquemment les puissances multiples de 3, qui correspondent aux préfixes du système international :

Table des puissances de dix multiples de trois

Puissance de dix négatives	Préfixe SI		Puissance de dix positives	Préfixe SI
10⁻³ = 0,001 un millième	m (milli-)		10³ = 1 000 mille	k (kilo-)
10⁻⁶ = 0,000 001 un millionième	µ (micro-)		10⁶ = 1 000 000 un million	M (méga-)
10⁻⁹ = 0,000 000 001 un milliardième	n (nano-)		10⁹ = 1 000 000 000 un milliard	G (giga-)
10⁻¹² = 0,000 000 000 001 un millième de milliardième	p (pico-)		10¹² = 1 000 000 000 000 mille milliard ou un billion (anglicisme)	T (téra-)
etc.	etc.		etc.	etc.

Si la virgule signale la position des unités dans l'écriture d'un nombre décimal, multiplier par 10 revient à déplacer la virgule d'un rang vers la droite et diviser par 10 revient à déplacer la virgule d'un rang vers la gauche. Donc multiplier par 10ⁿ pour tout entier positif n revient à déplacer la virgule de n rangs vers la droite ; diviser par 10ⁿ pour tout entier positif n revient à déplacer la virgule de n rangs vers la gauche. Ainsi,

• 325,72 × 10 = 3 257,2
• 325,72/10 = 32,572
• 325,72 × 10⁵ = 32 572 000
• 325,72/10⁵ = 0,003 257 2

Il faut savoir que ce sont la base des théories pour faire tous les calculs par la suite.

Les propriétés énoncées sur les puissances de a restent valables pour les puissances de 10.

L'utilisation des puissances de 10 intervient :

• dans l'écriture explicite en base 10 :

325,72 = 3·10² + 2·10¹ + 5·10⁰ + 7·10⁻¹ + 2·10⁻² ;

• dans l'écriture scientifique des nombres décimaux :

325,72 est noté 3,257 2 × 10²

où le nombre est écrit comme le produit d'un nombre, appelé mantisse, compris entre 1 et 10 (strictement inférieur à 10), avec une puissance entière de 10 appelée exposant ;

• et dans la notation ingénieur :

325,72 est noté 325,72

32 572 est noté 32,572 × 10³

où le nombre est écrit comme produit d'un nombre compris entre 1 et 999 compris, avec une puissance de 10 dont l'exposant est un multiple de 3.