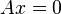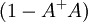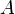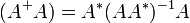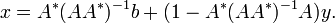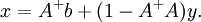Pseudo-inverse - Définition

Cas général pour une application linéaire

Définition et premières propriétés

Soient f une application linéaire entre deux espaces vectoriels E et F et g une application linéaire de F dans E. Ces deux applications sont pseudo-inverses l'une de l'autre si les deux conditions suivantes sont satisfaites :

et .

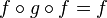
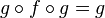
Dans ce cas, les propriétés suivantes sont vérifiées :

• l'espace E est la somme directe du noyau de f et de l'image de g ;
• l'espace F est la somme directe du noyau de g et de l'image de f ;
• les applications f et g induisent des isomorphismes réciproques entre leurs images ;
• si l'application f est inversible, alors son inverse est l'application g.

Cette définition se traduit naturellement sous forme matricielle.

Existence et construction

Réciproquement, soit f est une application linéaire entre deux espaces vectoriels E et F, dont le noyau admette un supplémentaire K dans E et dont l'image admette un supplémentaire N dans F. Alors la restriction de f à K induit un isomorphisme entre K et son image. L'application réciproque de l'image de f vers K s'étend de façon unique par l'application nulle sur N, en une application linéaire g de F dans E qui est par construction pseudo-inverse de f.

Il y a donc correspondance biunivoque entre les pseudo-inverses d'une application linéaire et les couples de supplémentaires pour son noyau et son image.

Remarque: ceci s'applique évidemment aux cas où l'un des supplémentaires K et N est réduit à l'origine, ce qui a lieu en particulier lorsque f est inversible: les deux sont alors réduits à l'origine.

Choix des supplémentaires

Il n'y a pas de choix canonique d'un supplémentaire en général, mais une structure d'espace euclidien ou hermitien sur les espaces vectoriels source et but permet d'en déterminer un par la définition de l'orthogonal. Cette définition du pseudo-inverse correspond au « pseudo-inverse de Moore-Penrose » pour les matrices.

Exemple d’utilisation

Le pseudo-inverse donne une solution à un système d’équations linéaires, équivalente à celle que donnerait la méthode des moindres carrés.

Soit un système Ax = b, on cherche le vecteur x qui minimise , où on a noté la norme euclidienne.

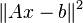
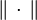
La solution générale à un système linéaire Ax = b est somme d'une solution particulière et de la solution générale de l'équation homogène Ax = 0.

Lemme : Si (AA ^* ) ^{− 1} existe, alors la solution x peut toujours être écrite comme somme des pseudo-inverses de la solution du système et d’une solution au système homogène :

Ici, le vecteur y est arbitraire (si ce n'est sa dimension). Le pseudo-inverse A ^* (AA ^* ) ^{− 1} apparaît deux fois : si on l’écrit , on obtient

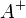
Le premier terme de la somme est la solution pseudo-inverse. Dans l’approche des moindres carrés, c’est la meilleure approximation linéaire de la solution. Cela signifie que le second terme de la somme est de norme minimale.

Ce second terme représente une solution au système homogène , puisque est la projection orthogonale sur le noyau de , alors que est la projection orthogonale sur l’image de A ^* .