Propagation des ondes radio - Définition

Dans l'espace

• Déplacement d'une onde électromagnétique dans l'espace

Les ondes provoquées par la chute d'un caillou à la surface d'un étang se propagent comme des cercles concentriques. L'onde radio émise par l'antenne isotropique (c'est-à-dire rayonnant de façon uniforme dans toutes les directions de l'espace) peut être représentée par une succession de sphères concentriques. On peut imaginer une bulle se gonflant très vite, à la vitesse de la lumière c, très proche de 300 000 km/s. Au bout d'une seconde, la sphère a 600 000 km de diamètre. Si le milieu de propagation n'est pas isotrope et homogène, le front de l'onde ne sera pas une sphère.

Dès que l'onde électromagnétique s'est suffisamment éloignée de sa source (à une distance de l'ordre de la longueur d'onde), on peut la considérer comme constituée par l'association d'un champ électrique E et d'un champ magnétique H. Ces deux champs oscillants sont perpendiculaires entre eux et perpendiculaires à la direction de propagation. Le rapport E/H entre l'amplitude de ces deux champs est égal à 377 ohms. La connaissance de l'un entraine la connaissance de l'autre. Pour cette raison, on définit en général l'amplitude de l'onde par l'amplitude de son champ électrique.

Comme une onde radio est une vibration, au bout d'une période, l'onde aura parcouru une distance notée lambda et appelée longueur d'onde. La longueur d'onde est une caractéristique essentielle dans l'étude de la propagation ; pour une fréquence donnée, elle dépend de la vitesse de propagation de l'onde.

On appelle polarisation d'une onde radio la direction du champ électrique. Par exemple, une antenne filaire verticale émettra une onde polarisée verticalement, c'est-à-dire avec un champ E vertical. Mais on peut trouver des ondes dont le sommet du vecteur E décrit une ellipse: La polarisation est elliptique. Une onde à polarisation elliptique peut être considérée comme la superposition des deux ondes "linéaires" polarisées à 90° l'une de l'autre.

• Variations du champ électrique

Plus on s'éloigne de l'antenne, plus l'intensité du champ électromagnétique rayonné est faible. Cette variation est régulière dans un espace homogène, dans le vide, par exemple. Dans ce cas, la puissance transportée par l'onde par unité de surface est inversement proportionnelle au carré de la distance à la source.( dès que l'on atteint une distance dite de Fraunhofer) Le champ électrique de l'onde est, lui, inversement proportionnel à la distance: le champ est divisé par deux si on se trouve deux fois plus loin. Pour calculer le champ à une distance D de l'antenne, il est important de définir si E désigne l'amplitude maximale du champ , ou bien la valeur efficace du champ. Il faut également définir l'antenne : doublet électrique élémentaire, dipôle demi-onde, antenne isotrope,etc..

Si P est la puissance ( non modulée) appliquée à un doublet électrique élémentaire, la valeur maximum du champ électrique E rayonné en un point situé à une distance D de cette antenne, perpendiculairement à l'antenne (sens du vecteur de Poynting), est donnée par la relation :

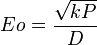
avec k = 90

Eo en V/m; P en W; D en m.

(Voir bibliographie : Goudet)

Ainsi, une puissance de 10W appliquée à ce doublet produira un champ d'amplitude maximum de 1 mV/m à une distance de 30 km, ce qui, en radioélectricité, n'est pas un champ négligeable.

Si on considère non plus un doublet électrique élémentaire ( qui n'a pas d'existence réelle) mais un dipôle demi-onde, le coefficient k sera égal à 98. Si on considère une antenne isotrope ( voir ci-dessous) , alors k = 60.

On utilise souvent, notamment en CEM, le concept d'antenne isotrope. Les calculs de champ sont d'abord effectués en fonction de l'antenne isotrope. On corrige ensuite le calcul en tenant compte du gain réel , en dB/iso, de l'antenne. Si on considère une source isotrope rayonnant une puissance P ( on dit alors que P est la P.I.R.E.), et si on considère le champ efficace (champ max divisé par racine de 2) alors on a la relation suivante :

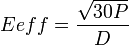
Ainsi, une puissance non modulée de 10 W appliquée à une antenne isotrope produira un champ E efficace de 5,7 V/m à une distance de 3 m.

Toutes ces relations ne sont valables que pour D suffisamment grand, dans la zone dite zone de Fraunhofer des éléments rayonnants. Cette zone commence à une distance de l'ordre de la longueur d'onde pour les antennes petites , mais peut être nettement plus éloignée pour les antennes à fort gain.

Dans les conditions réelles de propagation, on aura presque toujours des obstacles à proximité du trajet de l'onde, ou des éléments qui pourront provoquer des réflexions. En particulier, comme la terre est ronde, il y aura toujours une distance à laquelle la source d'émission n'est plus en visibilité de l'antenne de réception. Par exemple, en terrain plat, si les antennes d'émission et de réception sont distantes de 30 km, il faudra qu'elles soient à 15 mètres au-dessus du sol pour obtenir la visibilité optique . Et même dans ce cas, il y aura déjà une atténuation aux fréquences basses, du fait que l'ellipsoïde de Fresnel n'est pas dégagé aux fréquences basses.

Il faudra alors compter sur le phénomène de diffraction pour recevoir un signal, à moins que l'on soit dans le cas de réflexions ionosphériques (voir plus loin).

Pour une bonne réception, il est nécessaire que le champ électrique de l'onde captée ait un niveau suffisant. La valeur minimale de ce niveau dépend de la sensibilité du récepteur, du gain de l'antenne et du confort d'écoute souhaité. Dans le cas des transmissions numériques le confort d'écoute est remplacé par le taux d'erreur requis pour la transmission.

• Atténuation entre deux antennes

Dans le cas de la propagation en espace libre, c'est-à-dire ellipsoïde de Fresnel dégagé, et si les deux antennes ont même polarisation, il est possible de connaître le niveau de puissance reçu par une antenne de réception , en fonction de la distance à l'antenne d'émission et de la puissance de l'émetteur. Si l'antenne d'émission et l'antenne de réception sont isotropes ( gain 0db iso) , l'atténuation entre les deux antennes est:

A = 22dB + 20 log ( D/ lambda)

Par exemple, si une antenne isotrope reçoit de la part de l'émetteur une puissance PE de 10 W, à une fréquence de 150 MHz, on peut calculer ce que recevra une autre antenne isotrope placée à 1km:

lambda = 2m

PE = 10 w = 40 dBm

A= 22dB +20 log ( 1000/2) = 76 dB

PR = 40 dBm - 76 dB = -36 dBm

Ces formules avec l'antenne isotrope hypothétique permettent les calculs avec des antennes réelles, en tenant alors compte du gain /iso de celles -ci.

Pour plus de précisions, voir équation des télécommunications