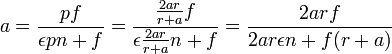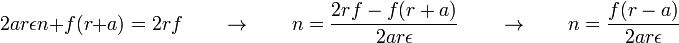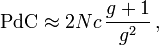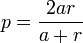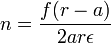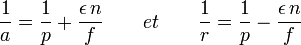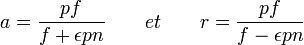Profondeur de champ - Définition

Profondeur de champ

Calcul de la profondeur de champ

Si la distance de mise au point est très supérieure à la focale

Premier plan net

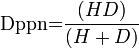
Dernier plan net pour D < H

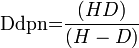
Si , la profondeur de champ est infini.

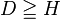
pour D < H

La profondeur de champ est :

PdC= Ddpn-Dppn

Soit :

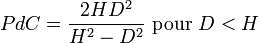
Où

• H est la distance hyperfocale
• D est la distance de mise au point

Avec pour l’hyperfocale

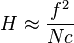
où

• f est la focale en mm.
• N est l'ouverture du diaphragme.
• c est la valeur du cercle de confusion en mm.

En remplaçant H par sa valeur on obtient :

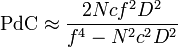
En première approximation N²c²D² peut être négligé

d'où

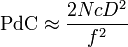
Pour un capteur donné, la profondeur de champ ne dépend que de la focale (f), de l'ouverture du diaphragme (N), et de la distance de mise au point (D)

Macrophotographie

À distance rapprochée, la formule de calcul de profondeur de champ est fonction du grandissement.

Ou :

• N est l'ouverture du diaphragme
• c est le cercle de confusion
• g est le grandissement

Recherche de réglages, connaissant l'objectif et la profondeur à obtenir

Si la netteté doit s'étendre de la distance a à la distance r, la mise au point doit être faite dans tous les cas à la distance :

avec comme ouverture maximale du diaphragme :

Exemple : on veut photographier un sujet dont les divers éléments intéressants sont compris entre 1,5 m et 3 m, avec un objectif de focale 50 mm (0,05 m) et une netteté angulaire de 1/1500.

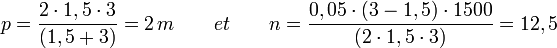
Le diaphragme est donc bien un instrument de mise au point !

En fait, faut-il avoir un ordinateur sous la main pour faire ce calcul ? Non, si l'objectif dont on dispose est muni d'une échelle de profondeur de champ !

De part et d'autre du losange qui sert de repère pour les échelles de distance et de diaphragme, on voit des traits symétriques portant des valeurs de diaphragme, 4, 8 et 16. En tournant la bague de mise au point de façon que les repères 1,5 m et 3 m deviennent symétriques par rapport au losange, comme par miracle, on fait la mise au point sur... 2 m. De plus, nos deux repères se trouvent quelque part entre les graduations d'ouverture 11 (nombre non gravé) et 16. Avec 12,5, notre calcul n'est apparemment pas si mauvais. Nous expliquerons plus loin ce petit « miracle ».

Recherche de la profondeur, connaissant l'objectif et les réglages

On peut au contraire rechercher les deux distances extrêmes a et r correspondant à un réglage donné de la mise au point et du diaphragme, pour un objectif donné :

ou si l'on préfère :

Au lieu de calculer, on peut aussi utiliser les échelles de l'objectif que l'on souhaite utiliser, s'il en possède, ce qui n'est évidemment pas le cas sur les appareils de bas de gamme.

Remarque 1 : vous lirez ou entendrez probablement un jour que la profondeur de champ est répartie pour un tiers devant le plan de mise au point et deux tiers derrière. En réalité, elle s'étend toujours davantage derrière que devant mais pas en proportions fixes : en macrophoto, les profondeurs avant et arrière sont presque égales mais pour le paysage, quand la netteté s'étend jusqu'à l'infini, la zone arrière est infiniment plus grande que la zone avant. Même si elle peut correspondre très grossièrement à des applications comme le portrait ou le nu en studio, la répartition 1/3 - 2/3 ne survient que dans des cas particuliers et mieux vaut oublier cette « loi » qui n'en est pas une.

Remarque 2 : vous trouverez peut-être dans d'autres ouvrages des formules un peu différentes, dans lesquelles les distances sont comptées non pas à partir du centre optique (ou du point nodal objet) mais à partir du plan du film. Cela ne change rien en pratique pour les sujets éloignés mais les résultats peuvent être très inexacts en macrophotographie.

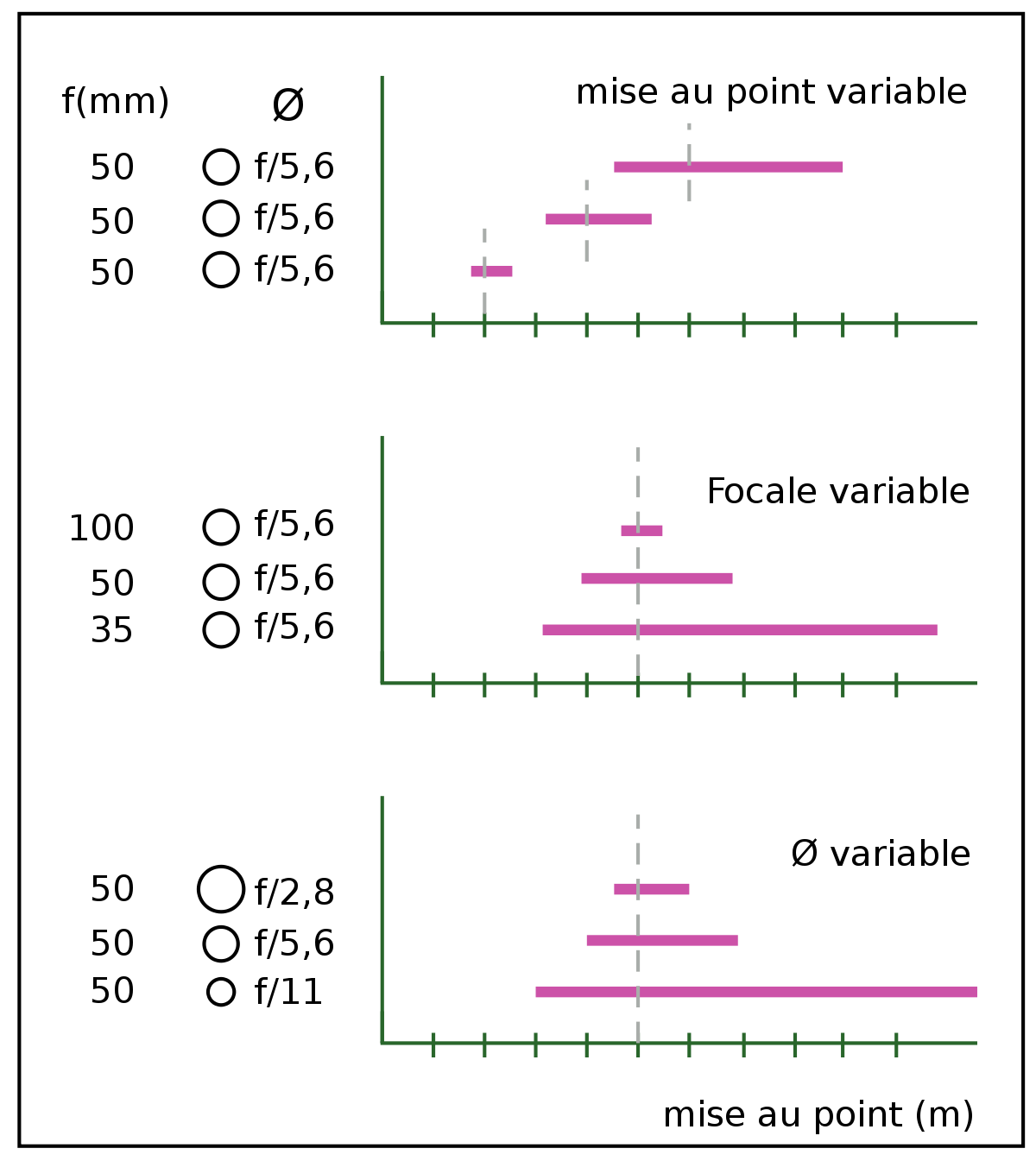
Profondeur de champ et distance focale

En pratique, contrairement à une idée reçue, la profondeur de champ ne varie pas avec la focale de l'objectif. En effet, si la focale était un paramètre pertinent pour régler la profondeur de champ, alors on verrait les photographes changer d'objectif ou actionner leur zoom pour obtenir une zone de netteté plus ou moins grande. Ce n'est évidemment pas le cas, puisque cette opération modifierait considérablement le cadrage. ^{[réf. souhaitée]}

En revanche si, d'un point de vue donné, en conservant le même angle de prise de vue et la même distance de mise au point, on veut photographier un même paysage avec plusieurs appareils de formats différents, alors les focales utilisées doivent être en proportion de ces formats (par exemple 10 mm pour un capteur de 6 x 9 mm, 40 mm pour un 24 x 36, 100 mm pour un 6 x 9 cm, etc.). Pour une même ouverture relative du diaphragme, on constate alors facilement que la profondeur de champ est d'autant plus grande que le format est plus petit, et inversement. La focale est en fait imposée par le choix d'un point de vue, d'un format de surface sensible et d'un cadrage, elle n'est qu'une conséquence de ces choix et c'est bien le format choisi qui est la cause première des variations constatées. Pour plus de détails, voir ce chapitre du wikilivre de photographie.

Avertissement

Les différentes formules que nous allons établir reposent sur des hypothèses bien définies mais souvent fort éloignées des situations pratiques, voire impossibles à respecter. C'est pourquoi nous envisagerons ensuite comment il convient de les utiliser de façon optimale ou même de les modifier pour tenir compte des situations concrètes.

Retenons l'avertissement sévère de Louis-Philippe Clerc (La Technique photographique, 2^e édition, 1934) : « On ne saurait trop insister sur le caractère arbitraire de tels calculs, basés sur la conception artificielle de rayons lumineux ; cette conception, destinée à faciliter l'application à l'optique des règles de la géométrie, même dans certains cas où elles ne sont plus applicables, amène fréquemment à des conclusions en antagonisme avec les prévisions de l'optique physique, dûment vérifiées par l'expérience ; en particulier, dans le cas considéré, l'optique géométrique ne tient pas compte d'un facteur essentiel, la répartition de la lumière à l'intérieur des taches-images. »

Les principaux résultats

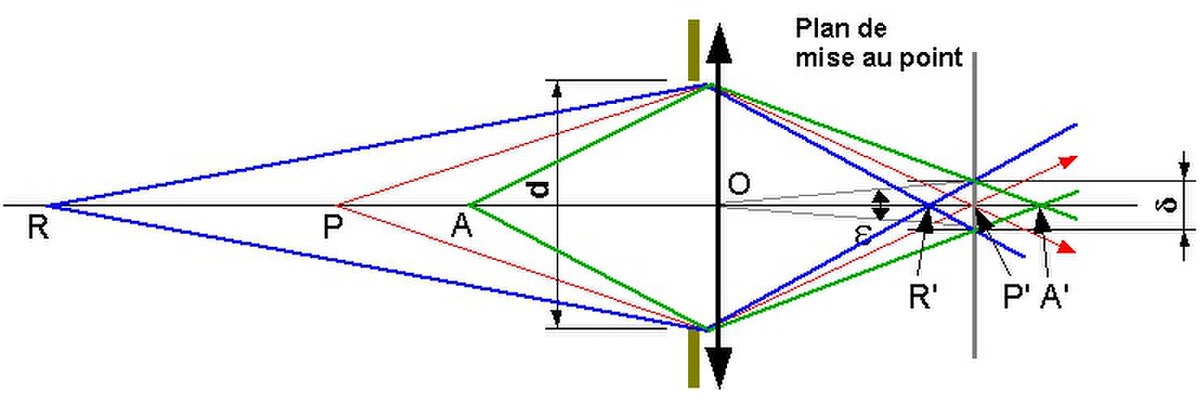
Nous disposons désormais de tous les éléments pour entrer dans le vif du sujet. Les hypothèses sont les mêmes que dans le cas précédent et les diverses distances seront notées conventionnellement OA=a, OA'=a', OP=p, etc. La mise au point a été faite à la distance du point P et la surface sensible calée très exactement sur le point P' où convergent les rayons issus de P.

• Les rayons issus d'un point extrême R, qui correspond à la limite éloignée de profondeur de champ, convergent en R' et poursuivent leur course jusqu'à la surface sensible où ils forment une tache de diamètre .
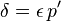
• Les rayons issus d'un point extrême A, qui correspond à la limite proche de profondeur de champ, convergeraient en A' s'ils n'étaient pas interceptés par la surface sensible, sur laquelle ils forment eux aussi une tache de diamètre .

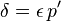
La portion de l'espace comprise entre les deux plans perpendiculaires à l'axe optique qui passent par A et R sera susceptible de fournir une image nette compte tenu des critères adoptés pour le calcul. L'espace qui sépare ces deux plans correspond à la profondeur de champ. Cette profondeur varie énormément avec le diaphragme, elle peut être quasi nulle si l'objectif est lumineux et grand ouvert et considérable s'il est fermé au maximum.

Les calculs complets figurent en annexe, pour les amateurs, à la fin de ce paragraphe. Ils sont un peu fastidieux mais ne présentent pas de difficulté particulière.

Annexes : le détail des calculs

Ce paragraphe n'est destiné qu'aux lecteurs qui s'intéressent à l'aspect mathématique des choses et sa lecture n'est pas indispensable pour comprendre la suite de cet exposé.

Calcul de a (ou r)

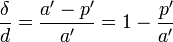
Les formules habituelles des lentilles simples permettent d'écrire :

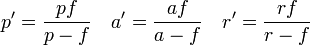
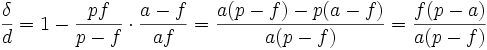
Par ailleurs

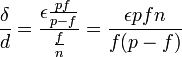
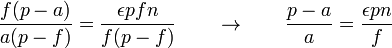
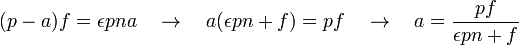
CQFD. Le calcul de r se conduit exactement de la même manière.

Calcul de p

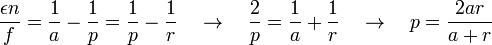
Calcul de n

On va partir de a et remplacer p par la valeur qui vient d'être calculée :