Produit vectoriel - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en géométrie, le produit vectoriel est une opération vectorielle effectuée dans les espaces euclidiens orientés de dimension trois. Le formalisme utilisé actuellement est apparu en 1881 dans un manuel d'analyse vectorielle écrit par Josiah Willard Gibbs pour ses étudiants en physique. Les travaux de Hermann Günther Grassmann et William Rowan Hamilton sont à l'origine du produit vectoriel défini par Gibbs.
Histoire
Résumé
En 1843, Hamilton inventa les quaternions qui permettent de définir le produit vectoriel. Indépendamment et à la même période (1844) Grassmann définissait dans Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik un « produit géométrique » à partir de considérations géométriques ; mais il ne parvient pas à définir clairement un produit vectoriel. Puis Grassmann lit Hamilton et s'inspire de ses travaux pour publier en 1862 une deuxième version de son traité qui est nettement plus claire. De même, Hamilton a lu les travaux de Grassmann et les a commentés et appréciés. Plus tard Maxwell commença à utiliser la théorie des quaternions pour l'appliquer à la physique. Après Maxwell, Clifford modifia profondément le formalisme de ce qui devenait l'analyse vectorielle. Il s'intéressa aux travaux de Grassmann et Hamilton avec une nette préférence pour le premier. En 1881, Gibbs publia Elements of Vector Analysis Arranged for the Use of Students of Physics s'inspirant des travaux déjà réalisés notamment ceux de Clifford et Maxwell. Si les physiciens se sont empressés d'utiliser le formalisme de Gibbs, celui-ci ne fut accepté en mathématiques que bien plus tard après plusieurs modifications.
Anecdote
Peter Guthrie Tait dans la préface de la troisième édition de son traité sur les quaternions qualifia le nouveau formalisme créé par Gibbs de « monstre hermaphrodite, composé des notations de Hamilton et Grassmann ».
Définition
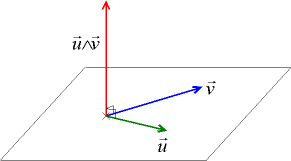
Soit E un espace vectoriel euclidien orienté de dimension 3. Par le choix d'une base orthonormée, E peut être identifié avec l'espace R3, mais cette identification n'est pas obligatoire pour définir le produit vectoriel.
D'un point de vue géométrique, le produit vectoriel de deux vecteurs
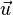
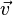
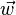
- le vecteur
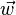
- la base
-
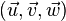
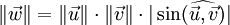
Lorsque les vecteurs sont colinéaires, leur produit vectoriel est nul.
La notion d'orientation peut ici être comprise de manière élémentaire en utilisant la règle de la main droite : le pouce, l'index et le majeur écartés en un trièdre indiquent respectivement le sens de u, de v et de w. Cette définition, utilisée dans l'enseignement secondaire, n'est pas totalement satisfaisante.
Définition par le produit mixte
Une seconde définition utilise la théorie des déterminants et la notion de produit mixte comme point de départ. Le produit mixte de trois vecteurs u,v,w, noté [u,v,w], est le déterminant de ces trois vecteurs dans une base orthonormale directe quelconque. La formule de changement de base montre que ce déterminant est indépendant du choix de la base ; géométriquement il est égal au volume orienté du parallélépipède appuyé sur les vecteurs u,v,w. Le produit vectoriel de deux vecteurs u et v est l'unique vecteur
-
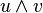
![\left[\vec u, \vec v, \vec w\right] = (\vec u \wedge \vec v) \cdot \vec w\,](https://static.techno-science.net/illustration/Definitions/autres/e/e3e94bd42adeb89556d444a062b694c4_235383d7f0e8425cce4294ee0e759328.png)
![\left[\vec u, \vec v, \vec w\right] = (\vec u \wedge \vec v) \cdot \vec w\,](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/e3e94bd42adeb89556d444a062b694c4_235383d7f0e8425cce4294ee0e759328.png)
L'existence et l'unicité d'un tel vecteur sont un cas particulier simple du théorème de représentation de Riesz. Le produit vectoriel s'interprète comme les variations du volume orienté d'un parallélépipède en fonction du troisième côté.
Avec une telle définition, il est possible de définir, dans un espace vectoriel orienté de dimension n + 1, le produit vectoriel de n vecteurs.
- Prenons la seconde définition ; et appliquons l'identité ci-dessus à w= u et v respectivement. On obtient :
-
-
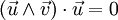
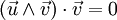
- Donc, le vecteur
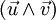
- De plus, si u,v,w forme une base directe, le produit mixte [u,v,w] est strictement positif. De fait,
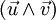
- Si w est de plus unitaire (de norme 1), alors
-
-
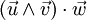
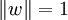
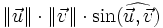
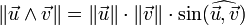
Calcul en composantes
Le choix d'une base orthonormée directe donne une identification de E et de ℝ3. Notons les coordonnées u=(u1, u2, u3) et v=(v1, v2, v3). Leur produit vectoriel est donné par :
Cette identité pourrait être prise comme une troisième définition, à condition de prouver que le vecteur obtenu est indépendant de la base orthonormale directe choisie pour le calculer.
Introduisons un vecteur w= (w1,w2,w3) et utilisons la définition par le produit mixte. Ce dernier est donné par :
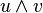
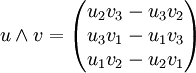
![[u,v,w]=\det\begin{pmatrix} u_1 & v_1 & w_1\\ u_2 & v_2 & w_2\\ u_3 & v_3 & w_3 \end{pmatrix}](https://static.techno-science.net/illustrationWebp/Definitions/autres/b/b35a324c858ffb60252bc5d7bc6f2b82_8889ebe20889fe4ba7f9064bc5924788.png)
En développant le déterminant par rapport à la troisième colonne :
-
![[u,v,w]=w_1\cdot\det\begin{pmatrix} u_2 & v_2 \\ u_3 & v_3 \end{pmatrix}-w_2\cdot \det\begin{pmatrix} u_1 & v_1 \\ u_3 & v_3 \end{pmatrix} +w_3\cdot\det\begin{pmatrix} u_1 & v_1 \\ u_2 & v_2 \\ \end{pmatrix}](https://static.techno-science.net/illustration/Definitions/autres/1/1a029d7e0b084f3ac4c6a40afa42399b_987585c8029027d56de5b600410e9bf4.png)
![[u,v,w]=w_1\cdot\det\begin{pmatrix} u_2 & v_2 \\ u_3 & v_3 \end{pmatrix}-w_2\cdot \det\begin{pmatrix} u_1 & v_1 \\ u_3 & v_3 \end{pmatrix} +w_3\cdot\det\begin{pmatrix} u_1 & v_1 \\ u_2 & v_2 \\ \end{pmatrix}](https://static.techno-science.net/illustrationWebp/Definitions/autres/1/1a029d7e0b084f3ac4c6a40afa42399b_987585c8029027d56de5b600410e9bf4.png)
Ce qui donne les coefficients de
