Produit scalaire - Définition
La liste des auteurs de cet article est disponible ici.
Généralisation aux espaces vectoriels complexes
Produit scalaire hermitien
Pour adapter la définition du produit scalaire réel aux espaces vectoriels complexes, nous avons besoin de la notion de « semi-linéarité » :
Une application f d'un espace vectoriel complexe 
dans 
est dite semi-linéaire si elle vérifie :
Soit donc maintenant 
un espace vectoriel complexe.
On dit qu'une application φ :
est un produit scalaire hermitien à gauche (ou simplement un produit scalaire) si elle est :
-
- sesquilinéaire à gauche : c'est-à-dire
-
- linéaire relativement au second argument (le premier étant fixé)
- semi-linéaire relativement au premier argument (le second étant fixé)
- symétrique hermitienne :
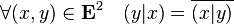
- positive :
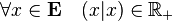
- définie :
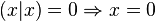
Remarque : la convention de linéarité à droite, semi-linéarité à gauche n'est pas universelle, certains auteurs utilisent la convention inverse. Dans un espace vectoriel complexe, muni d'un tel produit scalaire, sont encore vérifiés le théorème de Pythagore, l'inégalité de Cauchy-Schwarz et l'inégalité triangulaire.
Espace préhilbertien
Un espace préhilbertien est un espace vectoriel réel ou complexe, généralement de dimension infinie, que l'on a muni d'un produit scalaire. La définition du produit scalaire quitte alors le champ de la géométrie traditionnelle.
Exemples
- Dans l'espace
, on définit le produit scalaire canonique :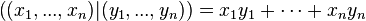 
.
- Dans l'espace
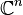, on définit le produit scalaire canonique : 
.
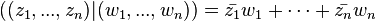- Soit
le 
-espace vectoriel des fonctions continues de l'intervalle ![[a,\, b]](https://static.techno-science.net/illustration/Definitions/autres/d/d2524b9940ce1c636bfb26ae09a941d2_de57359067f6b3298050b33ed863e8df.png)
dans .
- L'application
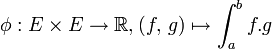est un produit scalaire sur E.
- Soit
![E=C([a,\, b],\mathbb{C})](https://static.techno-science.net/illustration/Definitions/autres/6/6a1ecef636c975ee4b38c1f179f891a9_5984fe9a088e8dcc226305b406efa238.png)
le -espace vectoriel des fonctions continues de l'intervalle dans ,
- L'application :
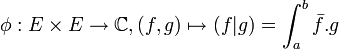est un produit scalaire sur . - .
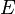Espace hermitien
Un espace hermitien est un espace vectoriel défini sur les nombres complexes, de dimension finie et disposant d'un produit hermitien, correspondant à une généralisation du cas réel. Le terme de produit scalaire est aussi utilisé dans ce contexte. Les résultats et propriétés des espaces euclidiens se traduisent souvent simplement dans cet espace.
Espace de Hilbert
Un espace de Hilbert peut être réel ou complexe. Il correspond exactement aux deux cas précédents, à la différence que la dimension n'est pas nécessairement finie. Si la théorie et les démonstrations sont différentes de la situation en dimension finie, certains résultats se généralisent. Une hypothèse topologique est néanmoins souvent nécessaire, celle de la complétude de l'espace métrique associé. Pour cette raison, un espace de Hilbert est par définition complet.
Cet espace est utilisé pour résoudre des problèmes d'analyse fonctionnelle, particulièrement des équations aux dérivées partielles.
Expression analytique
Base orthonormale
Dans un espace vectoriel de dimension deux ou trois, les propriétés algébriques permettent l'expression du produit scalaire à l'aide d'un système de coordonnées. Elle est plus simple si la base est choisie orthonormale, c'est-à-dire si ses vecteurs sont tous de norme égale à un et s'ils sont tous orthogonaux deux à deux. Par exemple en dimension trois, si la base orthonormale est notée (
, 
, 
), si les deux vecteurs 
et 
ont pour coordonnées respectives : (x1, x2, x3) et (y1, y2, y3), on obtient alors la formule :
Elle s'obtient à partir du développement des deux vecteurs dans la base :
Avec les propriété de bilinéarité et de symétrie, on montre que :
Or 
est égal à un car la base est normée et si i est différent de j alors 
est nul car la base est orthogonale.
Écriture matricielle
Il existe une manière simple d'exprimer le produit scalaire, à l'aide de matrice. les deux vecteurs et du paragraphe précédent prennent alors la forme suivante :
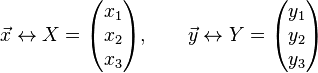
Les matrices X et Y représentent les deux vecteurs. À l'aide de l'opération transposée et de la multiplication des matrices, on obtient l'égalité :
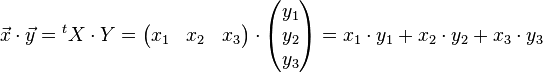
Base quelconque
Si la base (
, 
, 
) est choisie quelconque, l'expression du produit scalaire est plus complexe. Notons (φ1, φ2, φ3) et (ψ1, ψ2, ψ3) les coordonnées des vecteurs et dans cette nouvelle base. On a alors l'égalité :
La matrice M est appelée la matrice de Gram du produit scalaire dans la base (, , ). Elle possède de nombreuses propriétés, elle est symétrique suivant une diagonale, elle est donc diagonalisable, ses valeurs propres sont toutes strictement positives. Une telle matrice est dite matrice définie positive.
On montre que la donnée d'une matrice définie positive et d'une base dans un espace vectoriel réel de dimension n permettent de définir un produit scalaire de manière unique.