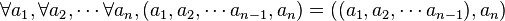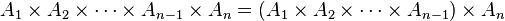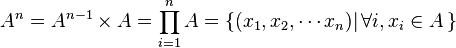Produit cartésien - Définition
La liste des auteurs de cet article est disponible ici.
Somme disjointe
Dans une réunion d'ensembles A∪B, l'origine des éléments y figurant est perdue. Un moyen d'éviter cette perte d'information est de réunir non pas directement les ensembles de départ, mais des copies de ces ensembles de la forme { α } × A et { β } × B , où « α » et « β » sont deux symboles quelconques distincts servant à identifier les ensembles A et B, par exemple « Ø » et « { Ø } », ou « 0 » et « 1 ».
L'union disjointe, encore appelée somme disjointe ou somme cartésienne de deux ensembles A et B est ainsi définie par :
On peut remarquer que la somme disjointe de deux ensembles vérifie également la propriété fondamentale des couples. De plus, contrairement aux couples de Kuratowski, cette notion, qui n'utilise que des opérations ensemblistes élémentaires, peut s'appliquer aux classes propres. C'est pourquoi les sommes disjointes sont parfois appelées couples généralisés, et utilisées ainsi en théorie des classes.
La somme disjointe peut se généraliser à plus de deux ensembles. Par exemple, pour trois ensembles quelconques A, B et C:
On rappelle que l'entier de von Neumann 2 peut se définir comme {Ø, {Ø}} . Plus généralement, l'entier de von Neumann n étant défini, l'entier de von Neumann n+1 est défini par n+1 = n ∪ {n}.
On peut donc généraliser ce qui précède et définir ainsi la somme disjointe de n ensembles
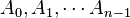
D'autre part cette définition de la somme disjointe utilise les entiers de la théorie des ensembles, non ceux du méta-langage. On peut donc également généraliser cette notion à des ensembles quelconques (non nécessairement finis) d'indices, par exemple des réunions disjointes dénombrables.
La définition de la somme disjointe souffre d'un arbitraire inessentiel. On peut définir la somme disjointe comme étant la réunion
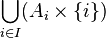
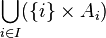
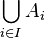
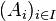
Généralisation à plus de deux ensembles
Triplets
Comme pour les couples, l'important, c'est leur propriété fondamentale : deux triplets sont égaux si et seulement si leurs premières composantes sont égales entre elles, puis leurs deuxièmes composantes, et enfin leurs troisièmes :
Là encore, cette propriété ne suffit pas à définir la notion de triplet, et là encore, plusieurs définitions incompatibles entre elles sont possibles a priori. On pose habituellement :
Produit cartésien de trois ensembles
Il est défini par :
D'après ce qui précède, A x B x C = ( A x B ) x C. Là encore l'ordre des termes est important. Le produit A x A x A est appelé cube cartésien de A et il est noté A3 (lire « A au cube ») :
Multiplets
Les définitions précédentes se généralisent par récurrence :
- Propriété fondamentale d'un multiplet d'ordre n, ou n-uplet :
- Définition d'un n-uplet :
- Produit cartésien de n ensembles :
- Puissance cartésienne n-ième d'un ensemble :
Note : en peut définir des produits cartésiens infinis (voir ci-dessous), mais pour le faire, nous avons besoin de la notion de fonction.
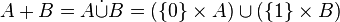
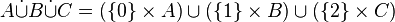
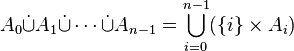
![\forall a , \forall b , \forall c , \forall d , \forall e , \forall f , [\, ( a , b , c ) = ( d , e , f ) \,] \Leftrightarrow [\, ( a = d ) \wedge ( b = e ) \wedge ( c = f ) \,]](https://static.techno-science.net/illustration/Definitions/autres/b/bef8730ac4c582baa5dd2c30cda5405f_67a3682058aaebe816611e21a776e39f.png)
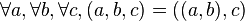
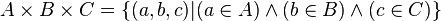
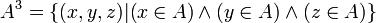
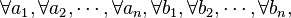
![[\, ( a_{1} , a_{2} , \cdots a_{n} ) = ( b_{1} , b_{2} , \cdots b_{n} ) \,] \Leftrightarrow [\, ( a_{1} = b_{1} ) \wedge ( a_{2} = b_{2} ) \wedge \cdots ( a_{n} = b_{n} ) \,]](https://static.techno-science.net/illustration/Definitions/autres/a/a56e56b787f7015fdcc47f29fb517597_5507b8dba0e92705f786c18681e5ea04.png)