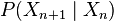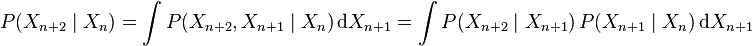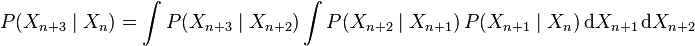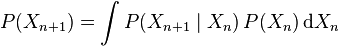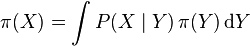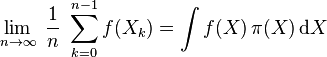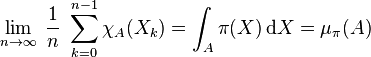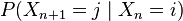Processus de Markov - Définition

Applications

• Les systèmes Markoviens sont très présents en physique particulièrement en physique statistique. Ils interviennent en particulier à travers l'équation de Fokker-Planck. Plus généralement l'hypothèse markovienne est souvent invoquée lorsque des probabilités sont utilisées pour modéliser l'état d'un système, en supposant toutefois que l'état futur du système peut être déduit du passé avec un historique assez faible.

• Le célèbre article de 1948 de Claude Shannon, A mathematical theory of communication, qui fonde la théorie de l'information, commence en introduisant la notion d'entropie à partir d'une modélisation Markovienne de la langue anglaise. Il montre ainsi le degré de prédictibilité de la langue anglaise, muni d'un simple modèle d'ordre 1. Bien que simples, de tels modèles permettent de bien représenter les propriétés statistiques des systèmes et de réaliser des prédictions efficaces sans décrire complètement la structure complète des systèmes.

• En compression, la modélisation markovienne permet la réalisation de techniques de codage entropique très efficaces, comme le codage arithmétique. De très nombreux algorithmes en reconnaissance des formes ou en intelligence artificielle comme par exemple l'algorithme de Viterbi, utilisé dans la grande majorité des systèmes de téléphonie mobile pour la correction d'erreurs, font l'hypothèse d'un processus markovien sous-jacent.

• L'indice de popularité d'une page Web (PageRank) tel qu'il est utilisé par Google est défini par une chaîne de Markov. Il est défini par la probabilité d'être dans cette page à partir d'un état quelconque de la chaine de Markov représentant le Web. Si N est le nombre de pages Web connues, et une page i a k_i liens, alors sa probabilité de transition vers une page liée (vers laquelle elle pointe) est et pour toutes les autres (pages non liées). Notons qu'on a bien . Le paramètre q vaut environ 0,15.

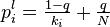
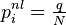
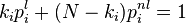
• Les chaînes de Markov sont un outil fondamental pour modéliser les processus en théorie des files d'attente et en statistiques.

• Les chaînes de Markov sont également utilisées en bio-informatique pour modéliser les relations entre symboles successifs d'une même séquence (de nucléotides par exemple), en allant au delà du modèle polynomial. Les modèles markoviens cachés ont également diverses utilisations, telles que la segmentation (définition de frontières de régions au sein de séquences de gènes ou de protéines dont les propriétés chimiques varient), l'alignement multiple, la prédiction de fonction, ou la découverte de gènes (les modèles markoviens cachés sont plus « flexibles » que les définitions strictes de type codon start + multiples codons + codons stop et ils sont donc plus adaptés pour les eucaryotes (à cause de la présence d'introns dans le génome de ceux-ci) ou pour la découverte de pseudo-gènes).

Propriétés des processus de Markov à temps discret

Un processus de Markov est caractérisé par la distribution conditionnelle :

qui est aussi appelée probabilité de transition d'un pas du processus. La probabilité de transition pour deux, trois pas ou plus se déduit de la probabilité de transition d'un pas, et de la propriété de Markov :

De même,

Ces formules se généralisent à un futur arbitrairement lointain n + k en multipliant les probabilités de transition et en intégrant k − 1 fois.

La loi de distribution marginale P(X_n) est la loi de distribution des états au temps n. La distribution initiale est P(X₀). L'évolution du processus après un pas est décrite par :

Ceci est une version de l'équation de Frobenius-Perron. Il peut exister une ou plusieurs distributions d'états π telles que :

où Y est un nom arbitraire pour la variable d'intégration. Une telle distribution π est appelée une distribution stationnaire. Une distribution stationnaire est une fonction propre de la loi de distribution conditionnelle, associée à la valeur propre 1.

Dans le cas des chaînes de Markov à espace d'états discret, certaines propriétés du processus déterminent s'il existe ou non une distribution stationnaire, et si elle est unique ou non.

• une Chaîne de Markov est irréductible si tout état est accessible à partir de n'importe quel autre état.
• un état est récurrent positif si l'espérance du temps de premier retour en cet état, partant de cet état, est finie.

Quand l'espace des états d'une chaîne de Markov n'est pas irréductible, il peut être partitionné en un ensemble de classes communicantes irréductibles. Le problème de la classification a son importance dans l'étude mathématique des chaînes de Markov et des processus stochastiques.

Si une chaîne de Markov possède au moins un état récurrent positif, alors il existe une distribution stationnaire.

Si une chaîne de Markov est récurrente positive et irréductible, alors :

• il existe une unique distribution stationnaire ;
• et le processus construit en prenant la distribution stationnaire comme distribution initiale est ergodique.

Donc, la moyenne d'une fonction f sur les instances de la chaîne de Markov est égale à sa moyenne selon sa distribution stationnaire :

C'est vrai en particulier lorsque f est la fonction identité.

La moyenne de la valeur des instances est donc, sur le long terme, égale à l'espérance de la distribution stationnaire.

De plus, cette équivalence sur les moyennes s'applique aussi si f est la fonction indicatrice d'un sous-ensemble A de l'espace des états :

où μ_π est la mesure induite par π.

Cela permet d'approximer la distribution stationnaire par un histogramme d'une séquence particulière.

Si l'espace des états est fini, alors la distribution de probabilité peut être représentée par une matrice stochastique appelée matrice de transition, dont le (i,j)^ème élément vaut :