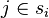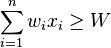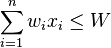Problème du sac à dos - Définition
La liste des auteurs de cet article est disponible ici.
NP-complétude
Le problème de sac à dos peut être représenté sous une forme décisionnelle en remplaçant la maximisation par la question suivante : un nombre k étant donné, existe-t-il une valeur des xi pour laquelle
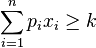
Sous sa forme décisionnelle, le problème est NP-complet, ce qui signifie qu'il n'existe pas de méthode générale connue pour construire une solution optimale, à part l'examen systématique de toutes les solutions envisageables. Le problème d'optimisation est NP-difficile, sa résolution est au moins aussi difficile que celle du problème de décision, et il n'existe pas d'algorithme polynomial connu qui, étant donné une solution, peut dire si elle est optimale (ce qui reviendrait à dire qu'il n'existe pas de solution avec un k plus grand, donc à résoudre le problème de décision NP-complet).
Procédé d'exploration systématique
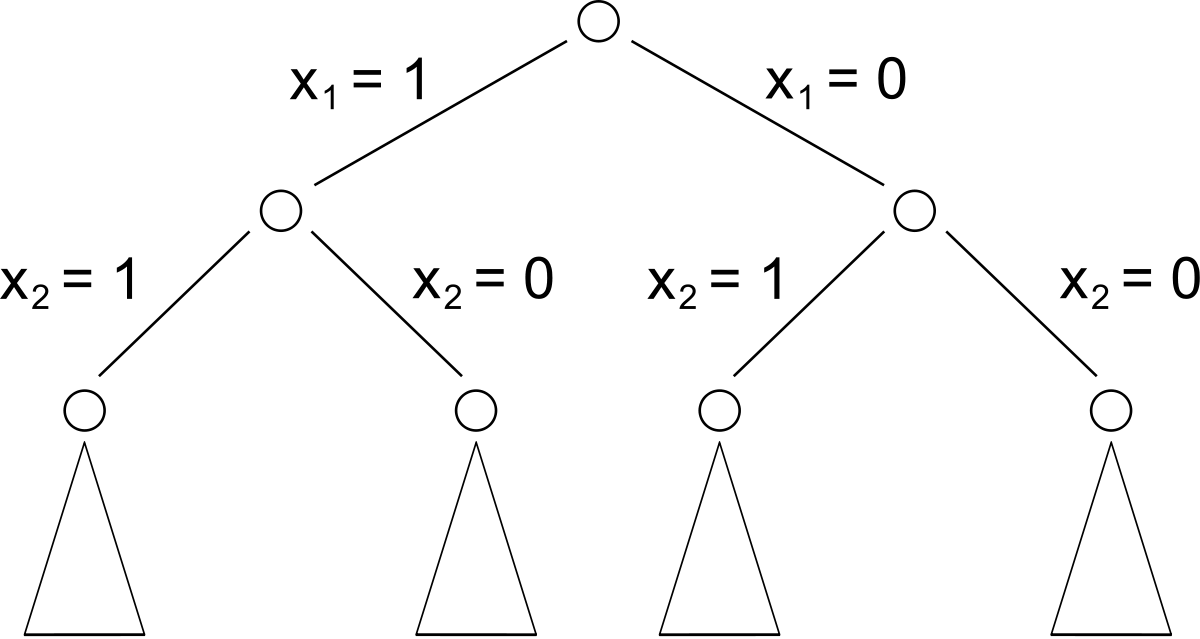
Cet examen systématique peut être réalisé à l'aide d'un arbre d'exploration binaire tel celui représenté ci-contre (les triangles représentent des sous-arbres).
L'arbre se décrit en descendant depuis le sommet jusqu'au bas des triangles (les feuilles de l'arbre). Chaque case correspond à un unique parcours possible. En suivant les indications portées le long des arêtes de l'arbre, à chaque parcours correspond une suite de valeurs pour x0,x1,...,xn formant un vecteur contenu. Il est alors possible de reporter dans chaque case la valeur totale et le poids total du contenu correspondant. Il ne reste plus qu'à éliminer les cases qui ne satisfont pas la contrainte, et à choisir parmi celles qui restent celle (ou une de celles) qui donne la plus grande valeur à la fonction objectif.
À chaque fois qu'un objet est ajouté à la liste des objets disponibles, un niveau s'ajoute à l'arbre d'exploration binaire, et le nombre de cases est multiplié par 2. L'exploration de l'arbre et le remplissage des cases ont donc un coût qui croît exponentiellement avec le nombre n d'objets.
Preuve de la NP-complétude
Cette preuve de NP-complétude a été présentée par Michail G. Lagoudakis reprenant un article de Richard Karp et un article de J.E. Savage.
La preuve de NP-complétude se fait en utilisant le problème de sac à dos sous la forme d'un problème de décision. Elle se fait en deux étapes, premièrement vérifier que (KP) appartient à la classe NP et, deuxièmement, montrer que (KP) est NP-difficile.
Nous utiliserons, pour la preuve d'appartenance à NP-difficile, la version somme de sous-ensembles (voir les variantes, plus bas), notée (SSE), une version particulière du sac à dos dans laquelle le profit d'un objet est égal à son poids. Si cette version particulière est NP-difficile, alors (KP) dans toute sa généralité l'est aussi.
Le problème (SSE) peut-être obtenu à partir du problème de sac à dos ci-dessus en posant wi = pi. En posant W = k, on obtient :
Trouver X tel que
Appartenance à NP
Premièrement, nous devons prouver que (KP) appartient à la classe NP, c’est-à-dire qu'il existe un algorithme polynomial qui, étant donné une solution au problème, peut vérifier que cette solution soit bonne. Pour vérifier une solution, il suffit de calculer la somme des poids des objets choisis et de la comparer avec W, ainsi que la somme de leurs valeurs, à comparer avec k. Le tout est évidemment polynomial. (KP) appartient donc à la classe des problèmes NP.
Appartenance à NP-difficile
Nous allons maintenant montrer que (SSE) est un problème NP-difficile en transformant le problème de la couverture exacte (noté (EC), de l'anglais exact cover) en un problème (SSE). Le problème (EC) s'exprime ainsi :
- Soit U un ensemble d'éléments et
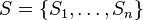
-
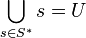
-
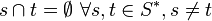
-
Le problème (EC) est NP-complet. Si nous arrivons à montrer que toute instance de (EC) peut être transformée polynomialement en une instance de (SSE) alors nous aurons prouvé que (SSE) (et donc (KP)) appartient à la classe des problèmes NP-difficiles.
Soit I = (U,S) une instance quelconque de (EC). Sans perdre de généralité, nous considérerons que
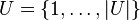
-
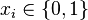
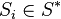
-
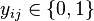
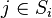
Soit b = | U | + 1. Les variables du problème (SSE) sont les xi du problème (EC). Nous définissons leur poids de la façon suivante :
-

Nous définissons la capacité W par
-
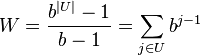
Le poids de l'objet i est une somme de puissances de b et bj − 1 apparaît dans wi si et seulement si