Problème de Monty Hall - Définition

Variantes

De nombreuses variantes ont été proposées, modifiant les paramètres. Il est souvent possible de trouver la solution de chaque problème par un raisonnement simple, comme dans le problème principal, mais la difficulté à saisir le rôle de chaque hypothèse conduit souvent à une réponse erronée, et il est donc préférable de d'abord résoudre le problème analytiquement.

Cas d'un nombre élevé de portes

Il est peut-être plus facile d'appréhender le résultat décrit ci-dessus en considérant 100 portes et non plus trois comme précédemment. Lorsque le candidat choisit une porte, il a 99 % de chances d'en choisir une avec une chèvre derrière. Inversement, la probabilité de tomber directement sur la porte cachant le prix de valeur est très faible (1 %). Imaginons maintenant que le présentateur ouvre, non plus une seule porte, mais 98 d'un coup, révélant bien évidemment 98 chèvres, tout en proposant toujours au candidat de changer son choix initial et de choisir la dernière porte restée close. À 99 % cette porte contiendra le prix de valeur, tout comme au début le candidat avait 99% de chances de choisir une porte avec une chèvre. Le candidat aura donc tout intérêt a changer son choix initial.

La démonstration est la même, mais le résultat est plus intuitif : il paraît tellement suspect que toutes les portes non choisies aient été ouverte sauf une.

On pourrait aussi laisser plus d'une des portes non choisies fermées, et même autoriser à sélectionner plus d'une porte au départ (le présentateur ne pourra ouvrir aucune des portes sélectionnées). Généralement, partant de n portes fermées, après que le candidat a désigné c porte(s), le présentateur ouvre m porte(s), m étant un entier entre 0 et n-c-1. Les chances d'être la bonne porte sont de:

• 1/n pour une des c porte(s) choisie(s) initialement
• pour chacune des autres portes.

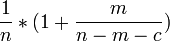
Il est équivalent d'ouvrir m portes une par une si le candidat refuse entre chaque ouverture de changer un de ses choix ou d'ouvrir les m portes en même temps.

Ces formules s'obtiennent par calcul avec un arbre, mais on peut les trouver immédiatement en utilisant le fait que quand les portes ont à l'origine toutes la même probabilité de cacher la voiture, l'ouverture laisse les probabilités inchangées pour les portes choisies à l'origine.

Soudoyons les organisateurs

Jusqu'ici, nous avons toujours supposé que les portes avaient à l'origine une probabilité égale de cacher la voiture. Que se passe-t-il si ce n'est plus le cas?

On peut par exemple imaginer que le candidat a dragué l'assistant(e) du présentateur, qui lui a révélé que la porte de droite cache une chèvre. Mal avisé, le candidat choisit d'abord la porte du milieu. Le présentateur ouvre alors la porte de gauche. Quelles sont les probabilités?

• Si on a pleinement confiance dans l'assistant(e), 1 pour la porte centrale, 0 pour la porte de droite
• Si l'assistant(e) ignorait tout et prétendait savoir pour se rendre intéressant(e), le problème est équivalent au problème initial, 1/3 pour la porte centrale, 2/3 pour la porte de droite
• Si l'assistant(e) a cherché à induire le candidat en erreur, 0 pour la porte centrale, 1 pour la porte de droite

On trouve une formule générale en appliquant le théorème de Bayes: on numérote arbitrairement 1 la porte choisie à l'origine, 2 la porte ouverte par le présentateur et 3 la dernière porte; on note p_i la probabilité à l'origine pour que la porte i cache la voiture

les chances sont après ouverture de pour la porte 3 (avec changement) et de pour la porte 1 (sans changement).

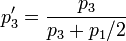
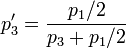
En fait, il est correct de dire que la porte choisie initialement a sa probabilité de cacher la voiture inchangée si elle est nulle ou bien si p₃ = p₂, ou plus généralement pour n portes si la probabilité moyenne des portes ouvertes pour cacher la voiture était égale à la probabilité moyenne des portes non choisies pour cacher la voiture.

Rappelons qu'il est équivalent de dire que la porte choisie initialement a sa probabilité de cacher la voiture inchangée ou que les portes non choisies non ouvertes ont hérité de la probabilité des portes ouvertes.

Changeons les règles d'ouverture

On doit à Jean-Paul Delahaye deux variantes qui éclairent bien sur l'importance des règles de l'ouverture de la porte. Dans un article de Pour la Science, il proposait que le présentateur ouvre une porte choisie au hasard parmi les deux portes non sélectionnées par le candidat (il peut éventuellement avoir décidé si la porte serait la plus à gauche ou à droite avant que le candidat ne désigne une porte), le jeu recommençant à zéro s'il ouvrait la porte cachant une voiture. Une seconde variante propose d'ouvrir une porte choisie au hasard parmi les deux portes cachant une chèvre, le jeu recommençant s'il ouvrait la porte sélectionnée par le candidat.

Delahaye affirma que les résultats de ces variantes étaient équivalents à ceux du problème original. Mais le courrier des lecteurs lui fit se reprendre : les probabilités sont de 1/3 pour que le changement soit gagnant, 1/3 pour que le maintien du choix initial soit gagnant, 1/3 pour qu'il y ait remise… Soit sur l'ensemble du jeu (après autant de remises qu'il aura fallu) 1 chance sur 2 de gagner quelle que soit la stratégie adoptée lors de la première manche non annulée.

On saisit ici l'importance des règles du jeu qui conditionnent l'ouverture d'une porte à la fois au choix du joueur et à la position de la bonne porte.

Introduisons encore quelques variantes pour mieux comprendre :

La porte ouverte par le présentateur est choisie parmi les 3 portes sans tenir compte ni du choix ni de la place de la voiture: on trouve cette fois 5 chances sur 9 de remise, 2 chances sur 9 de gagner en changeant, 2 chances sur 9 de gagner sans changer. Là encore, probabilité égale de gagner ultimement avec ou sans changement.

Le présentateur ouvre une des deux portes non choisies par le candidat, en choisissant 3 fois sur 4 la porte cachant la voiture si elle en fait partie: cette fois il y a une chance sur 2 de remise, 1 sur 3 de gagner sans changer et 1 sur 6 de gagner en changeant! Ultimement, 2 chances sur 3 de gagner sans changer. Eh oui, en biaisant les règles, on peut inverser l'efficacité des stratégies.

Plus généralement, s'il y a une probabilité p pour que la porte cachant la voiture soit ouverte (annulant la manche) quand elle n'a pas été sélectionnée, on 1/3 chance de gagner sans changer, 2*(1-p)/3 chance de gagner en changeant, 2p/3 chance de remettre en jeu. Ultimement, il y a 1/(3-2p) chance de gagner sans changer, 1-1/(3-2p) en changeant.

Dernière variante : le présentateur ouvre une porte ne cachant pas la voiture et non choisie par le candidat, mais pas au hasard: au contraire, il ouvre systématiquement la plus à droite des portes répondant aux précédents critères. Cette fois, si on choisit la porte du milieu :

• Si la bonne porte est une des deux plus à gauche, le présentateur ouvre la porte de droite
• Si la bonne porte est celle de droite, le présentateur ouvre la porte de gauche.

Donc, la probabilité de gagner en changeant n'est plus de 2/3 mais de 1 ou de 1/2 selon les cas, l'espérance totale restant de 2/3.

Généralisons encore: si la porte qui a été ouverte avait une probabilité p d'être ouverte s'il y avait le choix, la probabilité de gagner est de 1/(1+p) en changeant et de p/(1+p) sans changer. Avantage toujours au changement.

Formule globale

Donnons une formule globale pour toutes les variantes des deux paragraphes précédents. On notera:

concernant les probabilités avant ouverture (ces probabilités peuvent traduire par exemple le fait que le candidat est presque sûr d'avoir entendu une chèvre derrière une porte):

• p_c la probabilité pour la porte initialement choisie soit la bonne
• p_o la probabilité pour la porte qui est ensuite ouverte soit la bonne
• p_t la probabilité pour la troisième porte soit la bonne

Et on a p_c + p_o + p_t = 1 (et même p_c = p_o = p_t = 1 / 3 dans le problème traditionnel)

quand la porte choisie initialement est mauvaise:

• o_c la probabilité pour que le présentateur choisisse d'ouvrir la porte initialement choisie par le candidat (annule la manche, o_c = 0 dans le problème traditionnel)
• o_v la probabilité pour que le présentateur choisisse d'ouvrir la porte cachant la voiture (annule la manche,o_v = 0 dans le problème traditionnel)
• o_t la probabilité pour que le présentateur ouvre la troisième porte (o_t = 1 dans le problème traditionnel)

Et on a o_c + o_v + o_t = 1

quand la porte choisie initialement est la bonne

• o_i la probabilité pour que le présentateur ouvre la porte "interdite", choisie et cachant la voiture (annule la manche, o_i = 0 dans le problème traditionnel)
• o_o la probabilité qu'avait d'être ouverte la porte qu'il a justement ouverte quand il peut choisir (représente par exemple la préférence du présentateur pour la gauche, o_o = 1 / 2 dans le problème traditionnel)
• o_a la probabilité qu'avait d'être ouverte l'autre porte (même remarque que précédemment, o_a = 1 / 2 dans le problème traditionnel)

Et on a o_f + o_o + o_a = 1

Les probabilité sont:

• P(remise)= p_c * (o_i + o_t − 1) + 1 − o_t
• P(le jeu se termine à cette manche)= P_f = p_c * (1 − o_i − o_t) + o_t
• P(gain en changeant) =
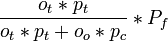
• P(gain en maintenant le choix initial) =

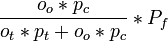
pour une manche

Et ultimement (en ayant remis en jeu autant de fois que nécessaire):

• P(gain en changeant) =
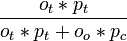
• P(gain en maintenant le choix initial) =

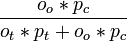
Les probabilités de gain final pour chacune des stratégie est égale à la probabilité de gain sur une manche sachant que cette manche aboutira.

Ces formules s'obtiennent sans trop de difficultés par calcul avec un arbre.

Problème quantique

Une variante audacieuse consiste à transposer le problème dans le monde de la physique quantique. Cette fois il ne s'agit plus d'ouvrir des portes mais de réaliser des mesures sur un système.

Sauf que cette fois comme on choisit un vecteur de mesure, les possibilités sont illimitées.

Les situations qui en résultent sont variables. Selon qu'on autorise le joueur seulement, le présentateur seulement ou les deux à utiliser à leur avantage les phénomènes, les probabilités sont plus ou moins en faveur du joueur.

Mais de façon un peu analogue au problème traditionnel, la mauvaise stratégie est de conserver son vecteur initial et la bonne est de choisir un vecteur orthogonal au vecteur initial.

http://xxx.lanl.gov/abs/quant-ph/0202120

Vous pouvez jouer vous-même à cette adresse: http://www.imaph.tu-bs.de/qi/monty/MontyS.html