Probabilité - Définition
La liste des auteurs de cet article est disponible ici.
Deux théorèmes de base des probabilités
Deux théorèmes mathématiques ont une place particulière en probabilité. Ces deux théorèmes sont la loi des grands nombres et le théorème central limite et sont présentés ici succinctement pour en faire comprendre l'intérêt et l'usage.
Loi des grands nombres
On ne présente ici que la loi forte des grands nombres mais il faut savoir que d'autre versions de lois des grands nombres existent.
Pour des variables aléatoires indépendantes, de même loi Xi et dont l'espérance existe:
Concrètement cette loi nous dit que la moyenne empirique d'une variable tend vers son espérance. Par exemple, pour un dé à 6 faces que l'on jetterait plusieurs fois de suite, la moyenne des lancers tend vers l'espérance 3,5.
Tendre vers est pris au sens presque sûrement, comme bien souvent en probabilité, c'est-à-dire que la probabilité que cela arrive est égale à 1. Comme esquissé dans les principes fondamentaux il peut très bien se faire que "exceptionnellement" cette moyenne ne tende pas vers l'espérance. On pourrait très bien, par exemple, ne tirer que des 1 lors des lancers de dés et que la moyenne soit alors 1 mais cela n'arrive "jamais". En général, si on lance des dés suffisamment de fois on tombera autant de fois sur chacune des 6 faces. Ce théorème formalise cette remarque de bon sens.
Théorème central limite
Ce théorème central limite est utile pour savoir comment une somme entre une réalisation d'une variable et la valeur moyenne se comporte. La loi des grands nombres montre que la moyenne des réalisations tend vers l'espérance. Quant au théorème central limite, il montre de quelle façon cette moyenne tend vers l'espérance. Une façon simple, mais pas très rigoureuse, d'écrire ce théorème permet de mieux comprendre son utilité:
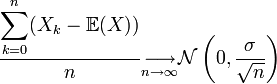
![]() est la loi normale de variance
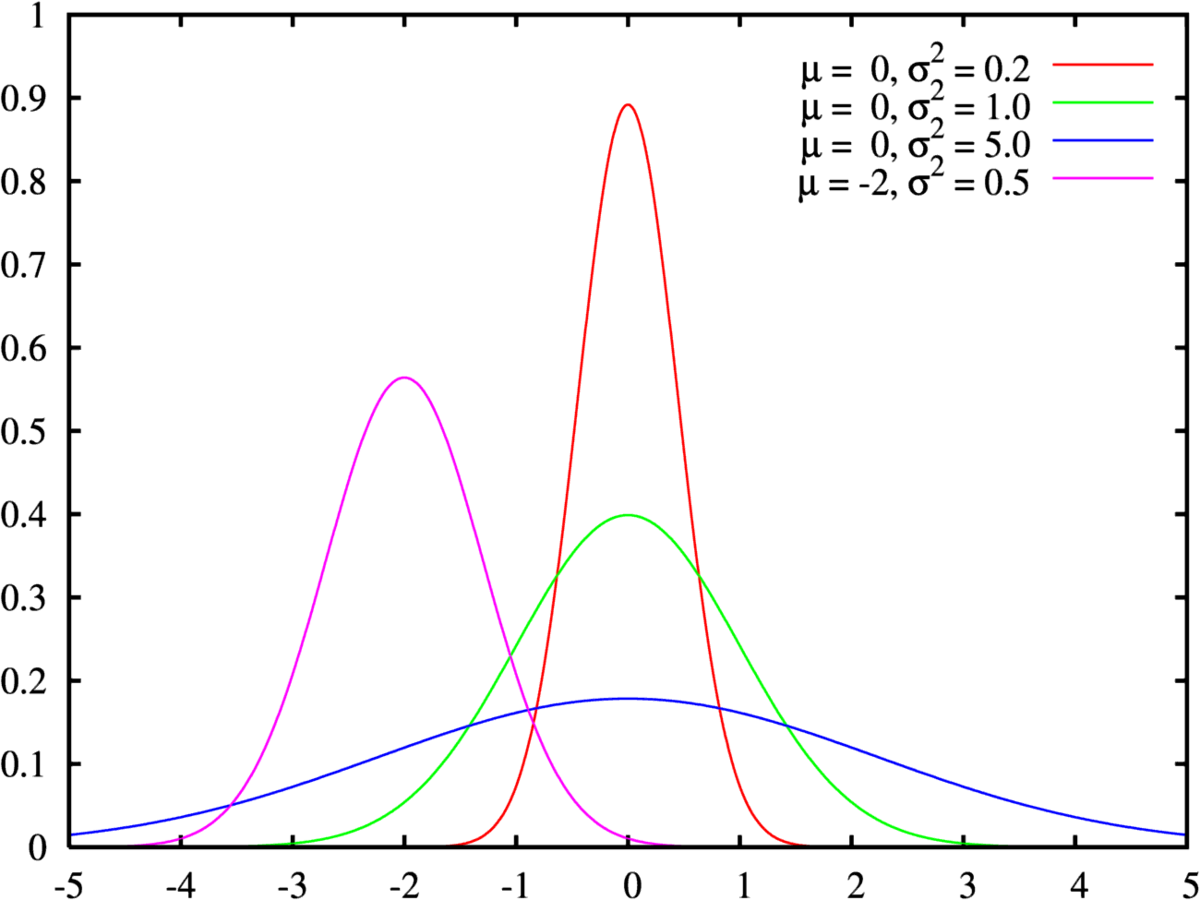
est la loi normale de variance ![]() , autrement appelée gaussienne et représentée ci-contre. Ce théorème a une très grande utilité en physique par exemple. Il peut se comprendre par « La moyenne des erreurs observées tend vers une loi normale. » La somme d'un grand nombre d'erreurs sur des observations par exemple est presque gaussienne. Elle serait gaussienne si on sommait une infinité d'erreurs mais en pratique cela n'est pas souvent le cas. La loi gaussienne fournit alors une approximation pour la loi de l'erreur souvent plus facilement utilisable que la loi exacte qui n'est pas tout le temps connue. De plus bon nombre de phénomènes naturels sont dus à la superposition de causes nombreuses, plus ou moins indépendantes qui se somment entre elles. Il en résulte que la loi normale les représente de manière raisonnablement efficace.
, autrement appelée gaussienne et représentée ci-contre. Ce théorème a une très grande utilité en physique par exemple. Il peut se comprendre par « La moyenne des erreurs observées tend vers une loi normale. » La somme d'un grand nombre d'erreurs sur des observations par exemple est presque gaussienne. Elle serait gaussienne si on sommait une infinité d'erreurs mais en pratique cela n'est pas souvent le cas. La loi gaussienne fournit alors une approximation pour la loi de l'erreur souvent plus facilement utilisable que la loi exacte qui n'est pas tout le temps connue. De plus bon nombre de phénomènes naturels sont dus à la superposition de causes nombreuses, plus ou moins indépendantes qui se somment entre elles. Il en résulte que la loi normale les représente de manière raisonnablement efficace.
Pour être plus correct, il faudrait écrire le théorème central limite de la façon suivante:
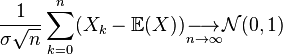
où la limite est prise au sens de tendre en loi, c'est-à-dire que la distribution de terme de gauche tend vers la distribution d'une gaussienne.
Il faut également savoir qu'il existe de nombreuses généralisations de ce théorème, entre autres pour des variables qui ne seraient pas identiquement distribuées (conditions de Liapounov ou conditions de Lindeberg) ou pour des variables de variance infinie (due à Gnedenko et Kolmogorov)
Le calcul stochastique
Un processus stochastique, est un processus aléatoire qui dépend du temps. Un processus stochastique est donc une fonction de deux variables: le temps et la réalisation ω d'une certaine expérience aléatoire.
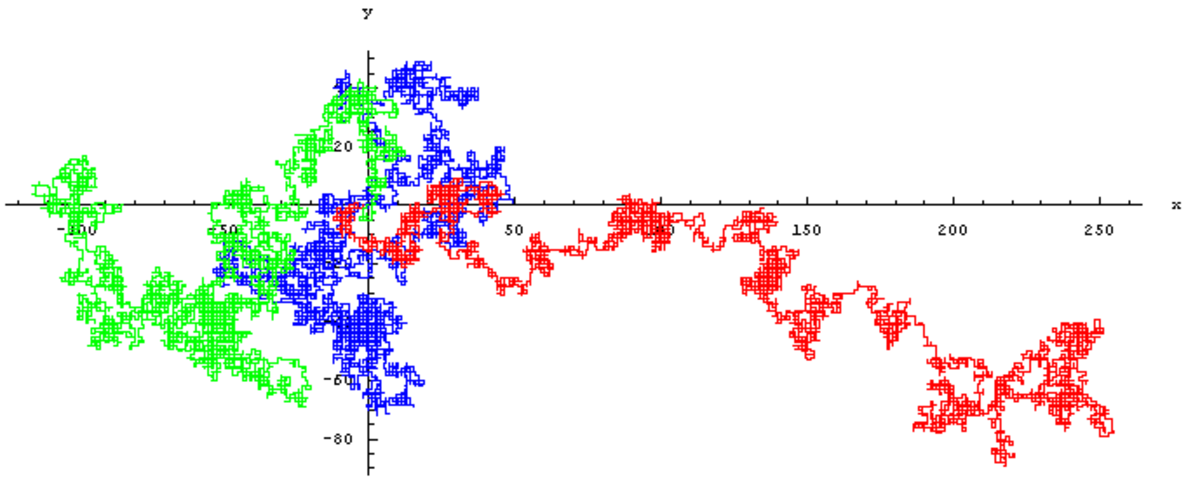
Parmi les processus stochastiques les chaînes de Markov constituent sans doute celui avec le plus d'applications pratiques. Ce sont des processus pour lesquels la prédiction du futur à partir du présent ne nécessite pas la connaissance du passé. Ces chaînes de Markov permettent de modéliser des phénomènes pour lesquels il suffit de connaître l'état présent pour pouvoir prévoir ce qui va se passer.
Ceci s'oppose, par exemple, à la notion d'hystérésis en physique où l'état actuel dépend de l'histoire et non seulement de l'état actuel. Les chaînes de Markov sont, entre autres, liées au mouvement brownien et à l'hypothèse ergodique, deux sujets de physique statistique qui ont été très importants au début du XXe siècle. Ils ont depuis connu d'autres utilisations pour étudier, par exemple, les fluctuations du marché boursier, ou pour la reconnaissance vocale. En temps discret, les processus stochastiques sont aussi connus sous le nom de Séries temporelles et servent entre autres en économétrie où ils ont une importance particulière.