Probabilité - Définition

Applications

Les jeux de hasard sont l'application la plus naturelle des probabilités mais de nombreux autres domaines s'appuient ou se servent des probabilités. Citons entre autres:

• les statistiques, sont un vaste domaine qui s'appuie sur les probabilités pour le traitement et l'interprétation des données.
• La théorie des jeux s'appuie fortement sur la probabilité et est utile en économie et plus précisément en micro-économie.
• l'estimation optimale par usage de la loi de Bayes, qui sert de fondement à une grande partie des applications de décision automatique (imagerie médicale, astronomie, reconnaissance de caractères, filtres anti-pourriel).
• En physique ainsi qu'en biologie moléculaire l'étude du mouvement brownien pour de petites particules ainsi que les Équation de Fokker-Planck font intervenir des concepts s'appuyant sur le calcul stochastique et la marche aléatoire
• les mathématiques financières font un large usage de la théorie des probabilités pour l'étude des cours de la bourse et des produits dérivés. Citons par exemple le Modèle de Black-Scholes pour déterminer le prix de certains actifs financiers (notamment les options).
• les Etudes Probabilistes de Sûreté où l'on évalue la probabilité d'occurrence d'un événement indésirable. C'est devenu un outil d'évaluation des risques dans bon nombre d'installations industrielles.

Le calcul des probabilités

Il existe deux façons de calculer les probabilités en mathématiques: le calcul a priori et le calcul a posteriori.

La première méthode, aussi appelée probabilité mathématique, part d'un calcul mathématique pour obtenir les probabilités. C'est le cas en particulier de la combinatoire, mais également des caractérisations de la loi exponentielle ou de la modélisation par une loi normale grâce à l'usage du théorème central limite. Ces méthodes ont en commun le fait qu'aucune expérience ne soit nécessaire pour déterminer les probabilités qui sont déterminées a priori.

La deuxième méthode est le calcul a posteriori, autrement appelé probabilité statistique, ces méthodes partent des résultats d'expériences pour déduire les probabilités. C'est le cas par exemple pour l'utilisation de la fréquence comme estimateur de la probabilité, du maximum de vraisemblance ou de l'Inférence bayésienne. Ces méthodes ont en commun le fait qu'une expérience soit nécessaire pour déterminer les probabilités qui sont déterminées a posteriori.

Nous présentons ici les principales méthodes permettant le calcul des probabilités.

L'usage de la combinatoire en probabilité

Certains problèmes de calcul de probabilité peuvent se ramener à un calcul de dénombrement, en particulier ceux pour lesquels il y a un nombre fini d'issues possibles à l'expérience et où la probabilité de chaque issue est la même. Cette méthode consiste à compter (dénombrer) le nombre total de cas possibles et le nombre de cas favorables à la réalisation d'un évènement.

Cette méthode permet par exemple de calculer la probabilité d'obtenir un 6 avec un dé équitable ou la probabilité d'obtenir un nombre pair, elle ne permet pas de calculer les probabilités avec un dé biaisé par exemple car alors la probabilité d'obtenir chaque face n'est plus la même. Cette méthode ne permet pas non plus de calculer la probabilité lorsqu'il y a un nombre infini de résultats possibles à l'expérience.

Estimateurs statistiques

Les estimateurs statistiques sont des valeurs calculées à partir d'un échantillon de la population totale ou d'un certain nombre de résultats de l'expérience aléatoires. Ces estimateurs sont souvent construits sur le principe du maximum de vraisemblance qui permet de construire tout une série d'estimateurs.

Parmi ceux-ci l'estimation par la fréquence d'apparition permet de déterminer la probabilité d'un évènement lorsqu'il y a un nombre fini d'évènements possibles et que l'on peut reproduire un grand nombre de fois et de façon indépendante l'expérience. Cet estimation peut, par exemple, servir pour obtenir la probabilité d'obtenir face ou un 6 avec un dé qu'il soit biaisé ou non. Il consiste à estimer la probabilité d'un évènement par sa fréquence d'apparition quand on répète un très grand nombre de fois l'expérience:

Par exemple si nous effectuons N lancers d'une pièce et que N_F représente le nombre de fois où la pièce tombe sur face, à mesure que N devient de plus en plus grand, nous nous attendons à ce que le rapport N_F/N devienne de plus en plus proche de 1/2. Cela nous suggère de définir la probabilité P(F) d'obtenir face comme étant la limite, quand N tend vers l'infini, de la suite des proportions :

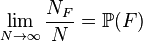
Cet estimateur pour la probabilité d'un évènement est, entre autres, un cas particulier de la loi des grands nombres en prenant par exemple la variable aléatoire X qui vaut 1 quand on obtient face et 0 sinon. Cette variable s'appelle la fonction caractéristique de F.

Des généralisations pour des variables continues existent par exemple la distribution empirique ou les estimateurs à noyaux. Ces estimateurs statistiques ont tous pour principal défaut le fait qu'il faut pouvoir répéter un grand nombre de fois l'expérience aléatoire ce qu'il n'est pas toujours possible de faire. Par exemple dans la pratique, nous ne pouvons pas lancer une pièce une infinité de fois.

Révision Bayésienne

La révision bayésienne est une autre méthode pour le calcul des probabilités. Elle est utilisée entre autres en théorie des jeux ou en intelligence artificielle pour créer des processus d'apprentissage. Elle se base sur la révision au fur et à mesure des expériences d'une croyance initiale (autrement appelée "probabilité a priori" quand cela n'entraine pas de confusion avec les probabilités a priori décrites dans l'introduction de cette section). Le choix de cette croyance initiale dépend des contraintes imposées à la distribution de probabilité. On choisit de toutes les distributions compatibles avec les contraintes celle d'entropie maximale, car c'est celle qui contient le moins d'information ajoutée Nous présentons seulement ici le mécanisme qui permet de réviser cette croyance initiale. Celle-ci se fait grâce au théorème de Bayes:

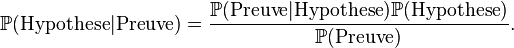
Dans cette version la croyance initiale est P(hypothèse). C'est la probabilité qu'une certaine hypothèse se vérifie. Cette croyance initiale est alors révisée grâce à une preuve que l'on peut observer. On en déduit une nouvelle probabilité que l'hypothèse initiale soit vérifiée en tenant compte de la preuve que l'on a observée. Ce processus s'appelle la "révision des croyances".

Notons ici que les termes Preuve et Hypothèse ont été choisis pour exprimer le lien qui devrait exister entre les deux événements et ainsi que le caractère asymétrique de ces deux événements. On aurait très bien pu prendre deux événements A et B par exemple. Dans la pratique il faut que l'événement "preuve" s'il se réalise rende plus probable (ou moins probable) la réalisation de l'événement "hypothèse" pour que cette méthode aboutisse. Ces deux événements ne doivent pas par exemple être indépendants.

Par exemple:

1. On se demande quel temps il fera demain. On regarde pour cela la météo. On connaît la probabilité que la météo a d'annoncer qu'il fera beau sachant qu'il fera effectivement beau: p(M|Beau)=0.9 et la probabilité que la météo annonce qu'il fait beau sachant qu'il pleuvra: P(M|Pleut)=0.2. Ces probabilités ont par exemple été estimées par d'autres méthodes sur l'année écoulée. L'événement M dénote ici le fait que la météo annonce du beau temps.
2. On part d'une croyance a priori sur le fait qu'il fera beau ou pas demain. Par exemple: P(Beau)=1/2 on croit a priori qu'il y a une chance sur deux qu'il fera beau demain. Ici notre hypothèse est le fait qu'il fera beau demain.
3. On estime P(M) la probabilité que la météo annonce qu'il fasse beau grâce à notre croyance initiale: la météo annonce qu'il fait beau dans 55% des cas. La probabilité qu'il fera beau demain sachant que la météo a annoncé beau temps est alors donnée par:

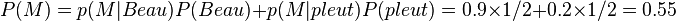
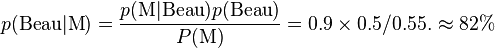
On pourrait alors, par exemple, réviser une deuxième fois l'hypothèse qu'il fera beau en regardant un deuxième bulletin météo d'une source différente. On prendrait alors comme croyance initiale la probabilité qu'il fasse beau que l'on vient de calculer.

Cette méthode permet de réviser la croyance que l'on a dans le fait qu'un événement futur va se passer. Cette méthode n'est employable que lorsque l'on a la possibilité d'estimer les probabilités conditionnelles p(M|Beau) p(M|pleut)

dans la formule donnée plus haut ainsi que pour calculer Cette méthode peut être utile car il est souvent plus simple de calculer les probabilités des observables conditionnées aux paramètres que de faire le contraire.

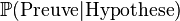
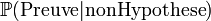
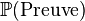
Interprétation des probabilités

Il existe deux façons de considérer les probabilités. La première historiquement a consisté à effectuer des calculs combinatoires dans le cas de jeux de hasard (Pascal, Bernoulli, Pólya…) cette approche peut se qualifier d'objective. La seconde, qui a commencé à se répandre vers 1974, est fondée sur le Théorème de Cox-Jaynes, qui démontre sous des hypothèses raisonnables que tout mécanisme d'apprentissage est soit isomorphe à la théorie des probabilités, soit incohérent. Dans cette seconde approche, la probabilité est considérée comme la traduction numérique d'un état de connaissance et donc une valeur subjective (mais néanmoins obtenue par un processus rationnel); la subjectivité s'explique par le fait que le contexte d'interprétation d'un événement diffère chez chacun. C'est l'école bayésienne.

L'idée de probabilité est le plus souvent séparée en deux concepts:

1. la probabilité de l'aléatoire, qui représente la probabilité d'événements futurs dont la réalisation dépend de quelques phénomènes physiques aléatoires, comme obtenir un as en lançant un dé ou obtenir un certain nombre en tournant une roue ;
2. la probabilité de l'épistémé, qui représente l'incertitude que nous avons devant des affirmations, lorsque nous ne disposons pas de la connaissance complète des circonstances et des causalités. De telles propositions peuvent avoir été vérifiées sur des événements passés ou seront peut-être vraies dans le futur. Quelques exemples de probabilités de l'épistémé sont, par exemple, assigner une probabilité à l'affirmation qu'une loi proposée de la physique est vraie, ou déterminer comment il est «probable» qu'un suspect ait commis un crime, en se basant sur les preuves présentées.

Une probabilité est-elle réductible à notre incapacité à prédire précisément quelles sont les forces qui pourraient affecter un phénomène, ou fait-elle partie de la nature de la réalité elle-même ainsi que le suggère la mécanique quantique ou la théorie du chaos ? La question reste à ce jour ouverte (voir aussi Principe d'incertitude).

Bien que les mêmes règles mathématiques s'appliquent indépendamment de l'interprétation choisie, le choix a des implications philosophiques importantes : parlons-nous jamais du monde réel (et a-t-on le droit d'en parler ?) ou bien simplement des représentations que nous en avons ? Ne pouvant par définition différencier le monde réel de ce que nous connaissons, il est bien entendu impossible de trancher de notre point de vue : la question est pour nous, par nature, subjective (voir aussi libre arbitre).

Des descriptions mathématiques rigoureuses de ce type de problèmes ne virent le jour que récemment, en particulier depuis

• Blaise Pascal au XVII^e siècle pour le déductif,
• Thomas Bayes et Pierre-Simon de Laplace au XVIII^e siècle pour l'inductif.

Pour donner un sens mathématique possible, et par ailleurs réducteur, à une probabilité, considérez une pièce de monnaie que vous lancez. Intuitivement, nous considérons la probabilité d'obtenir face à n'importe quel lancer de la pièce égale à 1/2 ; mais que signifie opérationnellement cette phrase ? Si nous lançons la pièce 9 fois de suite, la pièce ne pourra évidemment pas tomber « quatre fois et demie » de chaque côté; il est même possible d'obtenir 6 face et 3 pile, voire 9 face de suite. Que signifie dans ce cas le rapport 1/2 dans ce contexte et que pouvons-nous exactement en faire ?