Probabilité - Définition

Principes fondamentaux

La probabilité d'un certain évènement A, , est représenté par un nombre compris entre 0 et 1. Un évènement en probabilité peut être à peu près n'importe quoi pouvant se produire ou non. L'évènement A peut par exemple être le fait qu'il fasse beau demain, le fait d'obtenir un 6 avec un dé, voire le fait que le théorème de Pythagore soit vrai. Le seul impératif que l'on se fixe c'est de pouvoir vérifier si cet évènement se vérifie ou pas. On peut par exemple vérifier s'il fera beau demain, si on obtient un 6 ou si le théorème de Pythagore est vrai.

Un évènement impossible a une probabilité de 0 et un évènement certain a une probabilité de 1. Il faut savoir que le contraire n'est pas forcément vrai. Un évènement qui a une probabilité 0 peut très bien se produire dans le cas où un nombre infini d'évènements différents peut se produire. Ceci est détaillé dans l'article Ensemble négligeable et un exemple d'évènement de probabilité 0 et pouvant se produire est (rapidement) esquissé dans la partie loi des grands nombres. De même un évènement de probabilité 1 peut "exceptionnellement" ne pas se produire.

Probabilité et Réalité

Même si l'essence de la probabilité est la prédiction d'évènements du monde réel, la probabilité, n'étant qu'une théorie, ne peut pas nous renseigner sur la réalité. Comme dirait René Thom, prédire n'est pas expliquer...

Dans les faits, la probabilité s'occupe d'ensembles et de la mesure de ces ensembles. Dans un ensemble Oméga des possibles la probabilité du sous-ensemble A est sa mesure divisée par celle de Oméga. Pour l'exemple du dé ci-dessus, on a créé un ensemble Oméga ={1,2,3,4,5,6} de mesure 6, et avec A ={6}, la probabilité de A est 1/6. Le fait de créer ces objets mathématiques et de les relier à la réalité s'appelle modéliser, et toutes les vérités que l'on produit ne sont vraies qu'à l'intérieur du modèle. Seule l'expérimentation s'intéresse au lien entre la réalité et le modèle (les vérités mathématiques restent confinées au sein du modèle).

Ainsi, même si des pléthores d'expérimentations valident ou non chaque jour des myriades de modèles, rigoureusement, on ne peut affirmer que la probabilité qu'une pièce jetée en l'air retombe sur pile soit 1/2. Tout au plus, on peut faire cette hypothèse de modélisation. Mais cette hypothèse peut avoir diverses conséquences selon, par exemple, que l'on accepte ou non l'existence de l'infini. (Bien sûr, on peut imaginer l'infini en mathématique, la question qui reste ouverte est : cet infini a-t-il une existence concrète ? et peut-on envisager des modèles dans lequel il n'intervient pas ?) Supposons qu'une pièce a la probabilité 1/2 de faire pile, et 1/2 de faire face. Supposons de plus que l'on vient d'assister à 10 lancers de cette pièce sur pile. Oméga est l'ensemble des lancers possibles de cette pièce et A est l'ensemble des lancers possibles donnant un face. On sait que la mesure de A divisée par celle de Oméga vaut 1/2. La probabilité de faire face, après avoir assisté aux 10 lancers de pile est alors la mesure de A divisée par : la mesure de Oméga moins la mesure de l'ensemble B correspondant aux 10 lancers ayant donné pile. La probabilité dépend du choix de la mesure, mais si l'on n'accepte pas l'hypothèse de l'existence réelle de l'infini, la mesure qui s'impose dans un modèle est celle du dénombrement, on obtient alors que l'on a un peu plus de chances de faire un face qu'un pile si l'on vient d'assister à 10 réalisations de piles. (Cette probabilité est (M /2) / (M -10), où M est le nombre, que l'on ne connaît pas, des lancers possibles de la pièce). Ce modèle, bien sûr, n'est pas utilisable en pratique, et on pense communément qu'il est possible de lancer une pièce une infinité de fois. ("Possible" étant à prendre au sens le plus large, c'est-à-dire ici cela pourrait donner qu'il est possible que la pièce survive à la destruction de la Terre et continue d'être lancée par des extra-terrestres...) Avec cette hypothèse commune, il s'ensuit que la mesure de B devient négligeable (car c'est 10 devant l'infini) et que l'on a autant de chances de faire un face qu'un pile, même si l'on vient d'assister à 10 réalisations de piles. (C'est l'indépendance des évènements traitée ci-dessous.)

Finalement, penser que l'on a autant de chances de faire un face qu'un pile, même si l'on vient d'assister à 10 réalisations de piles, est donc une croyance et n'a aucun caractère de vérité en dehors d'un modèle probabiliste. Par-ailleurs, c'est le bon sens communément partagé, en l'occurrence celui qui nous fait penser que des lancers de pièces sont indépendants, qui impulse la théorie et qui rend le concept mathématique de l'infini pertinent. Et non l'inverse : on ne peut donc pas démontrer que, dans la réalité, les lancers de pièces sont indépendants. Ce sont en fait les probabilités qui sont conçues pour coller à cette hypothèse.

En dehors de toute considération métaphysique, l'infini et le continu doivent être considérés comme des concepts utiles en pratique. Ils aident à obtenir des modèles simples et pertinent face à la réalité. Par-exemple, chaque jour les professionnels de la bourse utilisent un modèle continu (le modèle Black-Scholes) alors que la réalité de la bourse appellerait une modélisation discrète mais trop compliquée, ou encore, en théorie des jeux certains modèles (de l'économie/sciences sociales), pour être suffisamment simples et réalistes, utilisent la notion de continuum de joueurs qui parait à première vue très loin de la réalité (au sein de laquelle le nombre de joueurs est fini). De même que pour modéliser notre lancer de pièce, l'infini est indispensable pour obtenir dans un cadre formel l'indépendance de deux lancers.

La notion d'indépendance

On dit que deux évènements sont indépendants lorsque le fait de connaître le résultat du premier évènement ne nous aide pas pour prévoir le second et inversement. C'est le cas lorsque la réalisation d'un évènement n'influence pas la probabilité que l'autre se réalise.

Par exemple lorsque l'on lance deux dés à la suite le résultat obtenu au premier dé ne va pas influencer le deuxième dé. Le fait de connaître le résultat du premier dé ne nous aide en rien pour prévoir le résultat du deuxième. On a toujours une chance sur 6 d'obtenir un 6 au deuxième jet de dé quel que soit le résultat du premier dé. Ce n'est pas parce que l'on a obtenu un 6 au premier jet de dé que cela change la probabilité d'obtenir un 6 au deuxième. Souvent si on mène deux expériences séparément (par exemple lancer un dé) le résultat de la première expérience n'influe pas sur la deuxième et on a alors une indépendance des résultats de la première expérience par rapport à la deuxième.

Cette notion d'indépendance intervient dans de nombreux théorèmes par exemple dans la loi des grands nombres et le théorème central limite exposés plus bas. En terme mathématique, deux évènements A et B sont indépendants si et seulement s'ils vérifient

où est la probabilité d'avoir à la fois A et B. On pourrait montrer grâce aux probabilités conditionnelles que cette définition recoupe bien l'idée que l'on se fait de l'indépendance.

On peut par exemple vérifier que la probabilité d'obtenir un 6 à un premier jet de dé est indépendante de celle d'obtenir un 6 à un deuxième lancer avec cette définition . La probabilité d'obtenir un 6 au premier dé vaut 1/6 (A), celle d'obtenir un 6 au deuxième dé vaut 1/6 (B). On peut grâce aux combinatoires montrer que la probabilité d'obtenir un double 6 vaut 1/36. On a alors:

Le fait d'obtenir un 6 au premier dé est donc bien indépendant du fait d'obtenir un 6 au deuxième dé.

Variable aléatoire

Une notion importante en probabilité est celle de variable aléatoire.

Les variables aléatoires furent introduites à l'origine pour représenter un gain. Par exemple effectuons l'expérience suivante, lançons une pièce de monnaie et suivant que le résultat est pile nous gagnons dix euros, ou face nous perdons un euro. On considère alors X, la variable aléatoire qui prend la valeur 10 lorsque nous obtenons pile et la valeur -1 lorsque nous obtenons face. X représente le gain à l'issue d'un lancer de la pièce.

De façon plus générale une variable aléatoire est une certaine fonction, qui dépend du résultat d'une expérience aléatoire par exemple dans ce cas le résultat du pile ou face. Cette fonction associe une certaine valeur au résultat d'une expérience. Dans notre exemple plus haut la variable aléatoire associe 10 à "pile" et -1 à "face". Cela permet d'associer des nombres à des résultats d'expériences qui ne sont pas numériques.

Le terme de variable aléatoire peut parfois être trompeur, en effet, ce n'est pas la valeur qu'elle prend une fois que l'on connaît le résultat de l'expérience qui est aléatoire, mais la valeur qu'elle va prendre avant d'avoir effectué l'expérience. Une fois que l'on connaît le résultat du pile ou face on connaît la valeur de X, notre gain, avec certitude et celle-ci ne dépend pas du hasard. Par contre, avant de jeter la pièce on ne sait pas quelle valeur va prendre X car on ne sait pas encore si l'on va obtenir pile ou face.

On ne considèrera ici que des variables aléatoires qui sont des nombres réels. De façon encore plus générale une variable aléatoire peut soit être un vecteur avec des coordonnées réelles soit un nombre réel. Il faut alors définir la loi jointe ainsi qu'une mesure sur un espace à plusieurs dimensions ce qui entraine des complications supplémentaires. Néanmoins pour des cas concrets on peut souvent se contenter de considérer plusieurs variables aléatoires qui dépendent de la même expérience. La restriction au cas de variables réelles n'est donc pas forcément aussi réducteur que l'on pourrait le penser.

Fonction de répartition et densité

Fonction de répartition de la loi normale centrée réduite

En probabilité, la fonction de répartition d'une variable aléatoire X est la fonction qui à tout réel x associe la probabilité que la variable X soit plus petite que x :

C'est une fonction croissante, allant de 0 à 1.

Pour les variables dont la fonction de répartition est absolument continue, on définit alors la densité de probabilité, qui est la dérivée de F par rapport à x :

La connaissance de la densité de probabilité permet notamment, en intégrant, de calculer la probabilité que X soit, par exemple, compris entre a et b.

L'espérance

L'espérance est un nombre qui se confond souvent avec la moyenne d'une variable, voir à ce sujet la loi des grands nombres ou le prochain paragraphe. C'est une valeur numérique permettant d'évaluer le résultat moyen d'une expérience aléatoire. On la définit par:

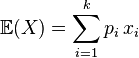pour une variable discrète (avec un nombre fini de réalisations possibles).

Par exemple, pour un dé à 6 faces, chaque face a une probabilité 1/6 d'apparaître et l'espérance vaut alors .

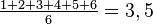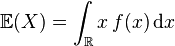pour une variable continue de densité f.