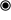Prisme triangulaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Prisme triangulaire uniforme | |
|---|---|

| |
| Type | Polyèdre semi-régulier |
| Éléments | F=5, A=9, S=6 (χ=2) |
| Faces par côtés | 3{4}+2{3} |
| Symbole de Schläfli | t{2,3} |
| Symbole de Wythoff | 2 3 | 2 |
| Coxeter-Dynkin |
|
| Symétrie | D3h |
| Références | U76(a) |
| Dual | Bipyramide triangulaire |
| Propriétés | convexe |
Figure de sommet 4.4.3 | |
Pour les prismes optiques, voir : Prisme (optique)
En géométrie, un prisme triangulaire ou prisme à trois côtés est un polyèdre fait à partir d'une base triangulaire, une copie translatée et 3 faces joignant les côtés correspondants.
Si les côtés sont des carrés, il est qualifié de polyèdre uniforme. En général, les côtés peuvent être des rectangles congrus.
D'une manière équivalente, c'est un pentaèdre dont deux faces sont parallèles, tandis que les normales aux surfaces des trois autres sont dans le même plan (qui n'est pas nécessairement parallèle aux plans des bases). Ces trois faces sont des parallélogrammes. Toutes les sections-croisées parallèles aux faces de la base sont le même triangle.
Un prisme triangulaire droit est semi-régulier si les faces des bases sont des triangles équilatéraux, et les trois autres faces sont des carrés.
Un prisme triangulaire droit général peut avoir des côtés rectangulaires.
Le dual d'un prisme triangulaire est une bipyramide à 3 côtés.
Le groupe de symétrie d'un prisme droit à 3 côtés avec une base régulière est le D3h d'ordre 12. Le groupe de rotation est D3 d'ordre 6.
Le groupe de symétrie ne contient pas d'inversion.
Volume
Le volume d'un prisme quelconque est le produit de l'aire de la base et de la distance entre les deux faces des bases. Dans ce cas, la base est un triangle, donc nous avons simplement besoin de calculer l'aire du triangle et de multiplier ceci par la longueur du prisme.
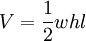
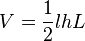
Aire de la surface
L'aire de la surface d'un prisme triangulaire est l'aire des trois côtés rectangulaires plus l'aire des deux triangles formant les bases.
bh + (s1 + s2 + s3)H
b=base
h=hauteur du triangle
s=longueur de côté
H=Hauteur du prisme
(s1+s2+s3)=périmètre de la base