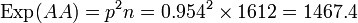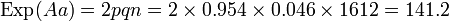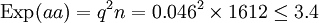Principe de Hardy-Weinberg - Définition

Introduction

Le principe de Hardy-Weinberg pour deux allèles : l'axe horizontal indique les deux fréquences d'allèle p et q, l'axe vertical indique la fréquence des génotypes et les trois génotypes possibles sont représentés par des glyphes différents

Le principe de (Castle-)Hardy-Weinberg ou la loi ou le modèle du même nom est une théorie qui postule qu'il y a un équilibre de la fréquence des allèles et des génotypes au cours des générations.

Hypothèses de départ

Pour que l'équilibre existe, plusieurs hypothèses sont décrites :

• La population est de taille infinie (~ grande taille, loi des grands nombres)
• Espèces diploïde et reproduction sexuée

• La Panmixie (croisements aléatoires entre individus) généralisée recouvre :
  • Équiprobabilité des gamètes : pangamie
  • Rencontre des gamètes au hasard ou formation aléatoire des couples ((Panmixie))**Ségrégation aléatoire des gamètes lors de la méïose

• Absence de migration
• Absence de mutation sur les allèles considérés
• Absence de sélection d'individus

• Les générations ne se chevauchent pas, seulement les individus.

Il faut cependant distinguer l'équilibre de (Castle-)Hardy-Weinberg de la structure de (Castle-)Hardy-Weinberg qui ne concerne pas la transmission des allèles d'une génération à une autre mais la relation entre fréquences alléliques et distribution des génotypes.

Causes de déviation

Quand les hypothèses du principe de Hardy-Weinberg ne sont pas réunies, ceci peut causer une déviation significative, c'est-à-dire que les fréquences génotypiques observées seront différentes des attendus théoriques. Les déviations observées peuvent être dues à un effet Wahlund, de la dépression de consanguinité, de la sélection pré-zygotique ou de la sélection post-zygotique ou enfin par dérive génétique.

Loi de distribution génotypique

De cet équilibre de Hardy-Weinberg, découle la loi de distribution génotypique :

p+q=1

(p+q)²=1

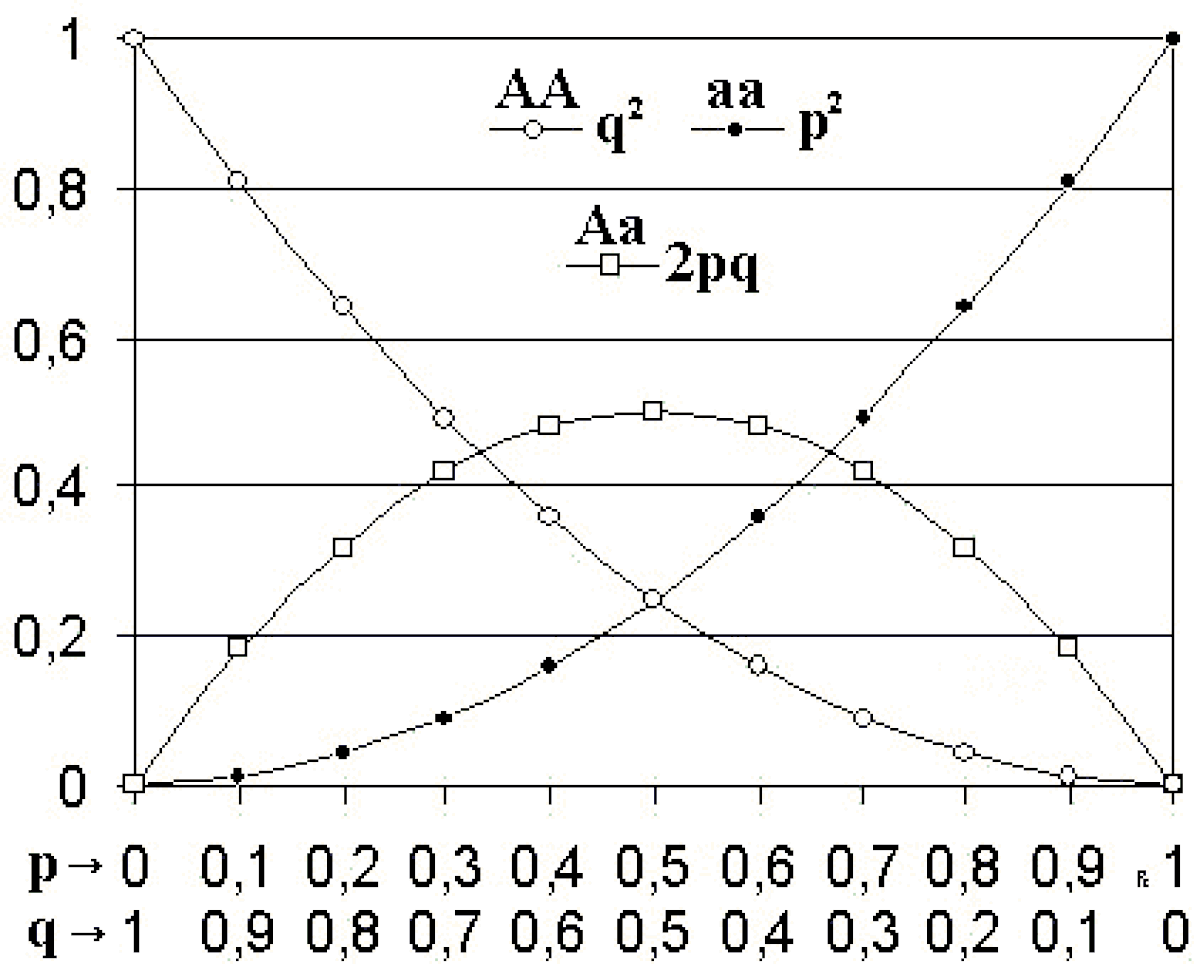
p² + q² + 2 pq = 1

Soit A et a, deux allèles de fréquence respectivement p et q.

Avec :

• p² :la fréquence d'un génotype homozygote AA pour deux alléles "A/"
• q² : la fréquence d'un génotype homozygote aa pour deux allèles "a/"
• 2pq : la fréquence d'un génotype hétérozygote Aa pour un allèle "A/" et un allèle "a/"

La loi d'Hardy-Weinberg est :

• Dans une population isolée d'effectif illimité, non soumise à la sélection, et dans laquelle il n'y a pas de mutations, les fréquences alléliques restent constantes.
• Si les accouplements sont panmictiques, les fréquences génotypiques se déduisent directement des fréquences alléliques et restent également constantes.

Cette loi décrit la structure génétique de nombreuses populations pour lesquelles les hypothèses de départ ne sont pas prospectées.

Applications

Calcul de fréquences géniques

Le calcul est simple lorsque les gènes sont codominants, il suffit de les compter à partir des phénotypes observés, dont le génotype est certain, et nous obtenons immédiatement une estimation des fréquences géniques.

Lorsque nous avons un ou des gènes récessifs, nous devons tenir compte des divers génotypes possibles.

Il en est ainsi du système de groupe sanguin ABO que nous prenons (d'après R.R. Race et R. Sanger, Les groupes sanguins chez l'homme, Masson 1970) pour exemple de calcul.

Le système ABO comporte 3 allèles, A, B, et O, ce dernier étant récessif. Par souci de simplification, nous ne différencions pas les 2 allèles A1 et A2 qui déterminent deux sortes différentes de groupe A, A1 étant dominant sur A2. Nous observons donc 4 phénotypes possibles. Nous observons, d'après M. goudemand et Ch. Salmon, les fréquences suivantes en France, arrondies à trois décimales :

A , fréquence 0.437, génotypes possibles A/A, A/O

B , fréquence 0.092, génotypes possibles B/B, B/O

AB, fréquence 0.036, génotype certain A/B

O , fréquence 0.435, génotype certain O/O

Soit a, b, o les fréquences géniques respectives des allèles A, B, O. Nous avons, par définition, a + b + o = 1

La fréquence du génotype O/O, égale à o² étant de 0.435, nous en déduisons la fréquence génique de o, soit : o = = 0.6595

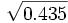
La fréquence génique de l'allèle A en découle, car nous avons la fréquence des sujets A = 0.437 = a² + 2ao = a² + 1.3190a d'où a = 0.2743

La valeur de b s'en déduit immédiatement ; b =1 -(0.6595 + 0.2743)= 0.0662

Ou plus simplement la méthode de Bernstein :

o = = 0.6595

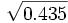
b = 1 - (a + o) = 1 - = 1 - 0.9338 = soit b = 0.0662

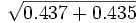
a = 1- (b + o) = 1 - = 1 - 0.7259, soit a = 0.2741

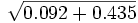
Le total o+a+b n'est pas égal exactement à 1, et certaines corrections doivent être apportées, et l'ont été tant par Bernstein, qu'ultérieurement par d'autres auteurs -Taylor et Prior (1938), R.A. Fisher et G.L. Taylor (1940), A.M. Dobson et E.W. Ikin (1946) et J.A.F. Roberts (1948) en ont publié les formules d'application.

Tests de signification pour la déviation

L'écart par rapport à la loi de Hardy-Weinberg est estimé grâce au Test du χ² de Pearson, en comparant la structure des fréquences génotypiques obtenues à partir des données observées, aux fréquences calculées selon la loi de Hardy-Weinberg. Lorsque les systèmes comprennent de nombreux allèles, certains génotypes peuvent manquer ou n'être observés qu'en petit nombre. Le test de χ² est alors inapplicable, ou des regroupements de classes doivent être effectués, et une méthode dérivée de la méthode exacte de Fisher doit être appliquée.

Exemple de test χ² pour la déviation

Les données suivantes ont été fournies par E.B. Ford (1971) qui a noté les phénotypes observés dans une population de papillons écaille rouge. Une faible discordance génotype-phénotype peut être négligée. L'hypothèse nulle est que cette population répond à la loi de Hardy-Weingerg, l'hypothèse alternative étant qu'elle n'y répond pas.

D'où les fréquences alléliques peuvent être estimées :

p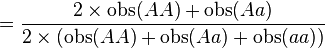
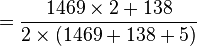
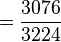
	= 0.954

et

q	= 1 − p
	= 1 − 0.954
	= 0.046

Les valeurs attendues sont :

Test du χ² :

χ2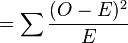
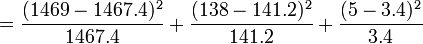
	= 0.001 + 0.073 + 0.756
	= 0.83

Il s'agit d'un test à un degré de liberté (ddl), -en règle, le nombre de degrés de liberté d'un test de χ² est de n − 1, où n est le nombre de classes, quoique qu'un autre ddl soit perdu, du fait que les valeurs attendues sont estimées à partir des valeurs observées. Le seuil de signification à 5% du χ², pour 1 ddl, est à 3.84. La valeur du χ² obtenue étant inférieure à 3.84, l'hypothèse nulle, à savoir la population étudiée suit la loi de Hardy-Weinberg, n'est pas rejetée.