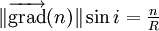Principe de Fermat - Définition

Bibliographie

• José Philipe Pérez, Optique : fondements et application
• Ouvrage de mécanique générale des Séries Schaum
• Born & Wolf, Principles of optics
• Georges Bruhat, Optique
• Jean Bass, Exercices de mathématiques, Masson, 1965, p. 381-385

Conséquences

Principe du retour inverse de la lumière

Le trajet suivi par la lumière pour aller d'un point à un autre ne dépend pas du sens de propagation de la lumière.

La stationnarité du chemin optique permet de procéder à quelques considérations. Entre deux points A et B, tous deux sur la trajectoire curviligne d'un rayon lumineux se propageant dans un milieu inhomogène, on peut exprimer l'intégrale de chemin optique comme il suit :

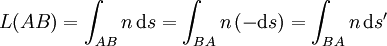
En considérant que ds' = − ds est l'élément de coordonnée curviligne de B vers A, on peut alors écrire L(AB) = L(BA). Dans le cas de l'étude d'un système optique, cela signifie que l'on pourra étudier la propagation de la lumière et le trajet des rayons lumineux sans se soucier du sens de propagation.

Attention : en pratique, l'utilisation irréfléchie de ce principe aboutit à des absurdités. On sait par exemple qu'un objectif ne donne jamais une image ponctuelle d'un point lumineux, mais une tache toujours plus ou moins floue. Il serait enfantin de penser que les rayons formant cette tache, renvoyés dans l'objectif par un miroir plan, pourraient reformer de l'autre côté un point-image net ... Ce n'est pas le principe qui est en cause ici, mais le fait de vouloir l'appliquer de façon fautive.

Lois de Snell-Descartes

Un plan P de vecteur normal sépare deux milieux d’indices de réfractions n₁ et n₂. Un rayon lumineux part d'un point A₁ situé dans le premier milieu, traverse P en M et atteint un point A₂. Le problème est de trouver la position de M à partir du principe de Fermat.

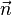
Le chemin optique de A₁ à A₂ est L = n₁A₁M + n₂A₂M donc

.

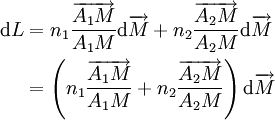
La condition de stationnarité de L, dL = 0, se traduit donc par le fait que est orthogonal au plan P, soit colinéaire à  ; le rayon lumineux est donc inclus dans le plan passant par A₁ et A₂ et orthogonal à P (première loi de Descartes) et donne : n₁sini₁ = n₂sini₂ (deuxième loi de Descartes).

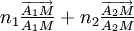
Cette démonstration est due essentiellement à Maupertuis en 1744, près d’un siècle après l’énoncé par Fermat de son principe.

Une jolie illustration en est donnée par le problème dit « du maître-nageur ». Celui-ci, situé sur la plage en A₁ doit aller secourir un noyé situé en A₂. Comme il court plus vite qu'il ne nage, son trajet optimal (en temps) est celui qui suit les lois de la réfraction, que nous venons de déterminer.

On démontre que si la surface de séparation des deux milieux est une surface quelconque, les deux lois de Descartes sont conservées (mais il peut y avoir plusieurs chemins possibles).

Généralisation des lois de Descartes au cas d’un milieu continu quelconque

Cas d'un trajet plan

En rapportant le plan à un repère Oxy, on a

 ;

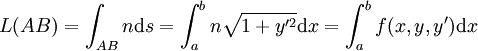
l’équation d'Euler-Lagrange du calcul des variations exprimant la stationnarité de cette intégrale s’écrit . Nous allons résoudre le cas particulier où n ne dépend que de x : on obtient alors , autrement dit  ; or si on désigne par i l’angle que fait la tangente à la courbe avec Ox, cette condition s’écrit :

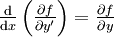
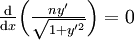
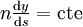
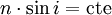
Ceci constitue en quelque sorte une version infinitésimale de la seconde loi de Descartes, laquelle est en fait une traduction locale du principe de Fermat.

L’équation différentielle de la trajectoire est donc : .

Traversée d'un rayon lumineux dans une bande où l'indice de réfraction est inversement proportionnel à la distance au centre de la bande : la trajectoire est un arc de cercle, comme démontré ci-contre.

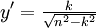
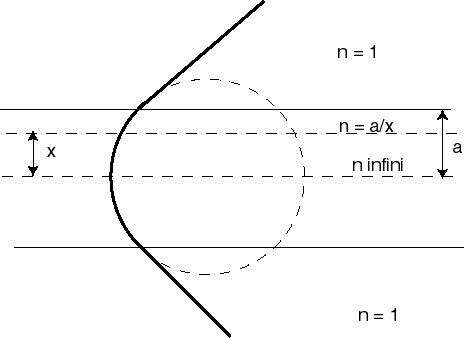
On retrouve évidemment que pour n constant, les trajectoires sont des droites ; mais si on prend , la courbe se paramétrise simplement en

.

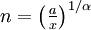
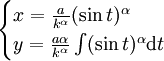
C'est une courbe de Ribaucour.

Par exemple pour α = 1 (l'indice de réfraction est inversement proportionnel à l'abscisse) on obtient

,

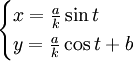
autrement dit les trajectoires sont des cercles.

Pour α = 2 (l'indice de réfraction est inversement proportionnel à la racine carrée de l'abscisse) on obtient

 :

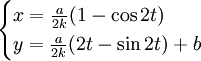
la courbe est une cycloïde. Ce cas est historiquement intéressant : c'est par cette méthode que Jean Bernoulli a prouvé que la courbe brachistochrone (minimisant le temps de parcours d'un point matériel) est la cycloïde, en montrant que le problème de mécanique et celui d'optique sont en fait équivalents.

Cas général

On considère maintenant un milieu inhomogène continu à 3 dimensions. On montre que les lois de Descartes généralisées, issues du principe de Fermat, s'énoncent sous la forme suivante :

1. Le plan osculateur à la trajectoire en un point M contient la normale à la surface d'indice de réfraction constant passant par M.
2. Si on désigne par i l’angle que fait la tangente à la courbe avec cette normale, on a la relation : où R est le rayon de courbure de la courbe.