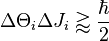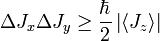Principe d'incertitude - Définition
La liste des auteurs de cet article est disponible ici.
Les relations de Heisenberg
Considérons une particule massive non relativiste se déplaçant sur un axe.
Description classique
La mécanique classique de Newton affirme que la dynamique de la particule est entièrement déterminée si l'on connaît à chaque instant : sa position x et sa quantité de mouvement p = mv (sa variation est également appelée : impulsion). Ces deux grandeurs physiques réelles ont des valeurs appartenant à

Description quantique
En mécanique quantique, la valeur précise des paramètres physiques tels que la position ou la vitesse n'est pas déterminée tant qu'elle n'est pas mesurée. Seule la distribution statistique de ces valeurs est parfaitement déterminée à tout instant. Cela peut mener au point de vue (qui est un abus de langage) selon lequel un objet quantique pourrait être "à plusieurs endroits en même temps". Un point de vue plus juste serait de dire que l'objet quantique n'a pas de localisation tant que la position n'est pas mesurée.
Cela dit, le paradoxe n'est qu'apparent. Il vient du fait que les grandeurs scalaires classiques sont insuffisantes pour décrire la réalité quantique. On doit faire appel à des fonctions d'onde qui sont des vecteurs appartenant à un espace de Hilbert de dimension infinie.
Les grandeurs classiques ne sont donc en fait que des vues partielles de l'objet, potentiellement corrélées.
Notion d'observable
Très curieusement, une grandeur physique, appelée une observable, n'est plus une fonction f (x,p) réelle, mais est représentée par un opérateur hermitien
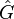

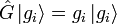
Si l'état du système à l'instant de la mesure est un vecteur


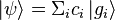
où les ci sont des nombres complexes.
Interprétation probabiliste
Le nombre complexe ci permet de calculer la probabilité pi d'obtenir la valeur gi :
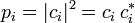
La mesure de la grandeur est donc une variable aléatoire (v.a.) avec une espérance E(g) et un écart type σ(g). La mesure est donc de nature probabiliste, ce qui implique beaucoup de paradoxes apparents en logique aristotélicienne. L'un d'entre eux a été immédiatement remarqué par Heisenberg : comme l'opérateur position

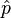
![\left[ \hat{x} , \hat{p} \right] = \hat{x}\, \hat{p} - \hat{p}\, \hat{x} = i \, \hbar](https://static.techno-science.net/illustration/Definitions/autres/a/a01c5934ce6dbd5a6fedad997faba133_5f097f0e981eb267635125b3c247342f.png)
Alors on ne peut pas mesurer simultanément ces deux grandeurs observables qui sont dits complémentaires. La notion d'espace des phases disparaît en mécanique quantique, et l'objet quantique est en fait complètement décrit par sa fonction d'onde. Les grandeurs scalaires utilisées en physique classique sont insuffisantes et inadéquates.
L'évolution déterministe de Newton est remplacée par une équation d'évolution déterministe de Schrödinger, permettant de prédire de façon certaine l'évolution temporelle des fonctions d'onde (dont le module carré est la probabilité, la phase n'étant pas connue a priori).
Inégalité de Heisenberg
Des mesures répétées de la position et de l'impulsion donneront des résultats en général différents à chaque mesure : chaque échantillon de valeurs sera caractérisé par un écart type : σx pour la position, et σp pour l'impulsion. Le théorème de Heisenberg démontre que :
-
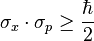
où

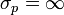
Principe général de Heisenberg
Le théorème de Heisenberg ne s’applique pas seulement au couple de valeurs position et quantité de mouvement. Dans sa forme générale, il s’applique à chaque couple d'opérateurs

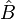
Énoncé du principe de Heisenberg
Pour un état

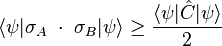
où la valeur moyenne du commutateur
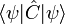

Ce théorème général, conséquence de l’inégalité de Cauchy-Schwarz, fut mis en évidence en 1930 par Robertson et (indépendamment) par Schrödinger ; l'inégalité est donc aussi connue comme la relation de Robertson-Schrödinger.
Principe ou théorème ?
Les puristes réservent parfois le nom de principe au cas où un minorant non nul de
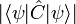

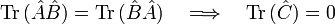
Il n'y a alors que théorème de Heisenberg, et non pas principe; c'est par exemple le cas d'un spin 1/2.
Autre formulation du principe de Heisenberg
L'inégalité de Heisenberg est souvent écrite :
![\Delta{A} \cdot \Delta{B} \ge \frac{1}{2} \left| \left\langle \left[ \hat{A}, \hat{B} \ \right] \right\rangle_\gamma \right|](https://static.techno-science.net/illustration/Definitions/autres/7/7cb2703eac36a28d1371aec39fb4f194_f49520ea2e338fb5dc1c842d7ec34737.png)
où :
- A et B sont deux observables,
-

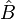
-
![[\hat{A},\hat{B}]](https://static.techno-science.net/illustration/Definitions/autres/c/c081d8bf21108f8283f018b863a75393_ebf9d1eeea34da9e2be0c39b3e1aae8b.png)

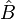
-
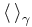
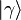
- Δ X est l’écart type de X :
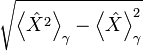
Relations qui impliquent le moment cinétique (ou angulaire)
Il existe des relations d'incertitude qui impliquent le moment cinétique quantique (ou moment angulaire). D'abord le moment cinétique est observable complémentaire à la position angulaire:
Aussi deux composantes orthogonales d'un même opérateur de moment cinétique sont complémentaires, par exemple:
En conséquence on ne peut mesurer qu'une seule composante du moment cinétique à la fois, normalement celle qui est parallèle à un champ externe (magnétique ou électrique) et qui est normalement à l'axe-z par tradition.
Relation temps-énergie
Il existe également une relation d'incertitude portant sur l'énergie d'une particule et la variable temps. Ainsi, la durée Δt nécessaire à la détection d'une particule d'énergie E à ΔE près vérifie la relation :
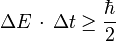
Cependant, la déduction de cette inégalité énergie-temps est assez différente de celle des inégalités position-impulsion. En effet, si le Hamiltonien est bien le générateur des translations dans le temps en mécanique hamiltonienne, indiquant que temps et énergie sont conjugués, il n'existe pas d'opérateur temps en mécanique quantique (« théorème » de Pauli), c’est-à-dire qu'on ne peut pas construire d'opérateur
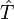
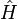
![\left[ \hat{H} , \hat{T} \right] = i \hbar](https://static.techno-science.net/illustration/Definitions/autres/3/3bf62205d69dab6392661a7c58723117_4bfa89cf9c3fd2e7ac9a4a44e7a45975.png)
ceci pour une raison très fondamentale : la mécanique quantique a en effet été inventée pour que chaque système physique stable possède un état fondamental d'énergie minimum.
Perspective historique
Il est clair que l'abandon de la logique d'Aristote à cause de la nature probabiliste de la mesure a suscité un vif émoi dans la communauté scientifique : John von Neumann est un des tout premiers à écrire sur la logique quantique, suivi par Mackey.
La controverse Einstein-Bohr est par ailleurs célèbre : pour Einstein, « Dieu ne joue pas aux dés ! », ce à quoi Bohr répondra : « Einstein, cessez de dire à Dieu ce qu'Il doit faire ». Le paradoxe EPR entraînera Bell, via ses inégalités, à renoncer à la notion classique de localité. Cette hypothèse sera confirmée par l'expérience d'Aspect en 1982; cette expérience sera encore raffinée par Anton Zeilinger en 1998. Le paradoxe du chat de Schrödinger conduira à une réflexion profonde sur le rôle du couplage à l'environnement et la décohérence des intricats. D'où la progression fulgurante de la cryptologie quantique, de la téléportation quantique, réalités techniques en 2005, et de l'informatique quantique, encore balbutiante en 2005.