Principe d'exclusion de Pauli - Définition
La liste des auteurs de cet article est disponible ici.
Utilisation en astrophysique
En astrophysique, l'effondrement d'étoiles à neutrons, qui demande aux neutrons un même mouvement, donc une même énergie, est limité par le principe d'exclusion qui explique ainsi en partie la cohésion de ces étoiles mortes extrêmement massives, qui, autrement, devraient s'effondrer sous l'effet de la gravitation.
Cependant, lorsque l'étoile est trop massive, le principe d'exclusion ne tient plus et alors l'étoile devient un trou noir.
Dérivation des principes de la mécanique quantique
Lorsque Pauli a proposé le principe d'exclusion (1925), les principes fondamentaux de la mécanique quantique n'étaient pas encore bien établis. En fait, il apparait que le principe d'exclusion n'est pas un principe fondamental et qu'il peut se dériver des principes fondamentaux de la mécanique quantique.
Voici une dérivation du principe d'exclusion de Pauli :
Soit un hamiltonien total, représentant l'état de 2 particules (l'extension à N particules est immédiate) :
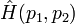
Si p1 et p2 sont deux particules indiscernables, alors
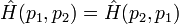
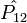
![[\hat{H},\hat{P_{12}}] = 0](https://static.techno-science.net/illustration/Definitions/autres/0/05c53138d6cbff790d588f10fbd4611b_b5040c1b67d7e685095c50d84712dfbb.png)
Le commutateur étant nul, il est possible de trouver une base dans laquelle ces deux opérateurs sont diagonaux : les solutions de
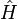
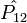
Comme
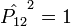
Les solutions symétriques : ψ(x1,x2) = ψ(x2,x1) ; x1 et x2 étant les coordonnées (position ainsi que spin) des particules 1 et 2. C'est le cas pour les bosons ou particules de spin entier.
Les solutions antisymétriques : ψ(x1,x2) = − ψ(x2,x1). C'est le cas pour les fermions ou particules de spin demi-entier, et donc pour le principe d'exclusion de Pauli.
Si on décompose la fonction d'onde totale des deux particules ψ(x1,x2) en intrication des états propres φa(xi) et φb(xi) de chaque particule, les solutions antisymétriques sont alors de la forme :
- ψ(x1,x2) = φa(x1)φb(x2) − φb(x1)φa(x2).
Si les particules 1 et 2 sont dans le même état quantique, alors φa = φb. La probabilité de trouver deux fermions identiques dans le même état quantique avec le même spin est nulle.
Ceci est le principe d'exclusion de Pauli : deux fermions identiques ne peuvent être dans le même état quantique avec le même spin.
Une autre conséquence de cette antisymétrie fait que la probabilité de trouver deux électrons de même spin à une même position instantanée est nulle, même sans supposer qu'ils occupent un même état quantique. Pour voir ceci on remarque que ψ(x1,x2) tend vers 0 quand x1 tend vers x2.
Particules échappant au principe d'exclusion
Seuls les fermions sont soumis à ce principe. Les particules indiscernables, de spin entier, satisfont à la statistique de Bose-Einstein et ils ne satisfont pas le principe d'exclusion de Pauli. Au contraire, on observera même un comportement « grégaire. »
Enfin, il existe des situations (particulièrement à deux dimensions), où l'on peut introduire des anyons, qui ne sont ni des fermions, ni des bosons.
D'autre part, la supersymétrie quantique associe à tout boson son supersymétrique fermion : ainsi au graviton, boson de spin 2, devrait être associé un gravitino de spin 3/2. En 2006, il n'existait encore aucune trace expérimentale de cette supersymétrie.
Énoncé relativiste
La version relativiste de la physique quantique prévoit l'existence de niveaux d'énergie négatifs : le principe d'exclusion permet d'expliquer pourquoi toutes les particules ne disparaissent pas dans ces niveaux-là — en effet, toute particule tend à aller vers l'état d'énergie le plus bas possible et donc devrait s'y précipiter. Si l'on considère comme le fit Dirac que tous les états d'énergie sont occupés,alors, ils ne peuvent pas être habités par d'autres fermions identiques.

















































