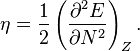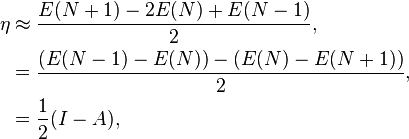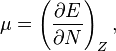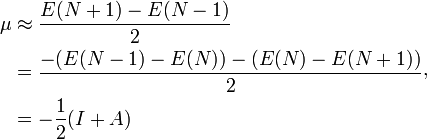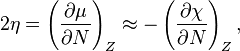Principe HSAB - Définition
La liste des auteurs de cet article est disponible ici.
Quantification de la dureté chimique
En 1983, Pearson travaillant avec Robert Parr a étendu la théorie qualitative HSAB avec une définition quantitative de la dureté chimique (η) qui est proportionelle à la seconde dérivée de l’énergie totale d’un système chimique selon les changements du nombre d’électrons dans un environnement nucléaire fixe:
Le facteur 1/2 est arbitraire et souvent omis, comme Pearson l’a noté.
Une définition opérationelle de la dureté chimique est obtenue en appliquant une approximation en différence finie sur trois décimales de la dérivée seconde:
où I est le potentiel d’ionisation et A l’affinité électronique. Cette expression implique que la dureté chimique est proportionelle à l‘écard de bande (band gap) d’un système chimique, quand un tel écart existe.
La première dérivée de l’énergie selon le nombre d’électrons est égale au potentiel chimique, μ, du système,
à partir duquel une définition opérationnelle du potentiel chimique est obtenu depuis une approximation en différence finie de la dérivée du premier ordre, soit :
qui est égal à la négation de la définition de l’électronégativité (χ) sur l’échelle de Mulliken :
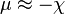
et dans ce sens, la dureté est une mesure de la résistance à la déformation ou au changement d’état. De même une valeur de zéro indique une molesse maximale, où la molesse est définie comme la réciproque de la dureté.
Dans les compilations de valeurs de dureté chimique ainsi calculées, seule celle des anions hydrure dévient du modèle initial. Un autre défaut noté dans l’article original de 1983 est l’apparente dureté du Tl3+ en comparaison du Tl+. Et cette valeur ne permet pas de discriminer totalement les acides mous et bases molles :
| Acides de Lewis | Bases de Lewis | ||||
|---|---|---|---|---|---|
| Hydrogène | H+ | infini | Fluorure | F– | 7 |
| Aluminium | Al3+ | 45,8 | Ammoniac | NH3 | 6,8 |
| Lithium | Li+ | 35,1 | Hydrure | H– | 6,8 |
| Scandium | Sc3+ | 24,6 | Monoxyde de carbone | CO | 6,0 |
| Sodium | Na+ | 21,1 | Hydroxyle | OH– | 5,6 |
| Lanthane | La3+ | 15,4 | Cyanure | CN– | 5,3 |
| Zinc | Zn2+ | 10,8 | Phosphane | PH3 | 5,0 |
| Dioxyde de carbone | CO2 | 10,8 | Nitrite | NO2– | 4,5 |
| Dioxyde de soufre | SO2 | 5,6 | Sulfhydryle | SH- | 4,1 |
| Iode | I2 | 3,4 | Méthane | CH3- | 4,0 |
Applications de la théorie
Quelques exemples illustrant l’adéquation de la théorie :
- Les métaux bruts sont des acides mous et empoisonnés par des bases molles comme les phosphines et sulfides.
- Les solvants durs tels que le fluorure d’hydrogène, l’eau et les solvants protiques tendent à dissoudre les bases fortement solubles telles que les anions de fluorine ou d’oxygène. D’un autre côté, les solvants aprotiques dipolaires tels que sulfoxyde de diméthyl et l’acétone sont des solvants mous avec une préférence à dissoudre des anions larges et des bases molles.
- Dans les réactions de complexation des ions de métaux de transition, de multiples expériences ont montré que la force des liaisons entre les centres métalliques et le ligands peuvent être expliquées par les principes de base dure, base molle, acide dur, acide mou et ordonnées selon leur molesse ou dureté.
| Acides de Lewis | Bases de Lewis | ||||||
|---|---|---|---|---|---|---|---|
| durs | mous | dures | molles | ||||
| Hydrogène | H+ | Mercure | Hg2+, Hg22+, CH3Hg+ | Hydroxyle | OH- | Hydrure | H- |
| Métaux alcalins | Li+,Na+,K+ | Platine | Pt4+ | Alcoolates | R-O- | Thiols | R-S- |
| Titane | Ti4+ | Palladium | Pd2+ | Halogénures | F-,Cl- | Halogénures | I- |
| Chrome | Cr3+,Cr6+ | Argent | Ag+ | Ammoniac | NH3 | Phosphine | P-R3 |
| Trifluorure de bore | BF3 | Borane | BH3 | Ion carboxylate | R-COO- | Thiocyanate | SCN- |
| Carbocation | R3-C+ | Métaux au d.ox. 0 | M0 | Carbonate | CO32- | Monoxyde de carbone | CO |
| Hydrazine | N2H4 | Benzène | C6H6 | ||||