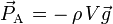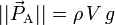Poussée d'Archimède - Définition

Formulation du théorème d'Archimède

« Tout corps plongé dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa surface libre, subit une force verticale, dirigée de bas en haut et opposée au poids du volume de fluide déplacé ; cette force est appelée « poussée d'Archimède ». »

Pour que le théorème s'applique il faut que le fluide immergeant et le corps immergé soient au repos. Il faut également qu'il soit possible de remplacer le corps immergé par du fluide immergeant sans rompre l'équilibre, le contre-exemple étant le bouchon d'une baignoire remplie d'eau : si celui-ci est remplacé par de l'eau, il est clair que la baignoire se vide et que le fluide n'est alors plus au repos. Le théorème ne s'applique pas puisque nous sommes dans un cas où le bouchon n'est pas entièrement mouillé par le liquide et ne traverse pas sa surface libre.

Une fois les conditions précédentes respectées, dans un champ de pesanteur uniforme, la poussée d'Archimède P est donnée par la formule suivante :

,

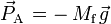
où M est la masse du fluide contenu dans le volume V déplacé, et g la valeur du champ de pesanteur.

Si la masse volumique ρ du fluide est elle aussi uniforme, on aura :

ou encore, si l'on considère les normes des forces :

La poussée d'Archimède P s'exprimera en newton (N) si la masse volumique ρ est en kg/m³, le volume de fluide déplacé V en m³ et la valeur de la pesanteur g en N/kg (ou m/s²).

Applications

Exemple d'un solide entièrement immergé

Trois solides de densités différentes peuvent subir une poussée d'Archimède inférieure, égale ou supérieure à leur poids.

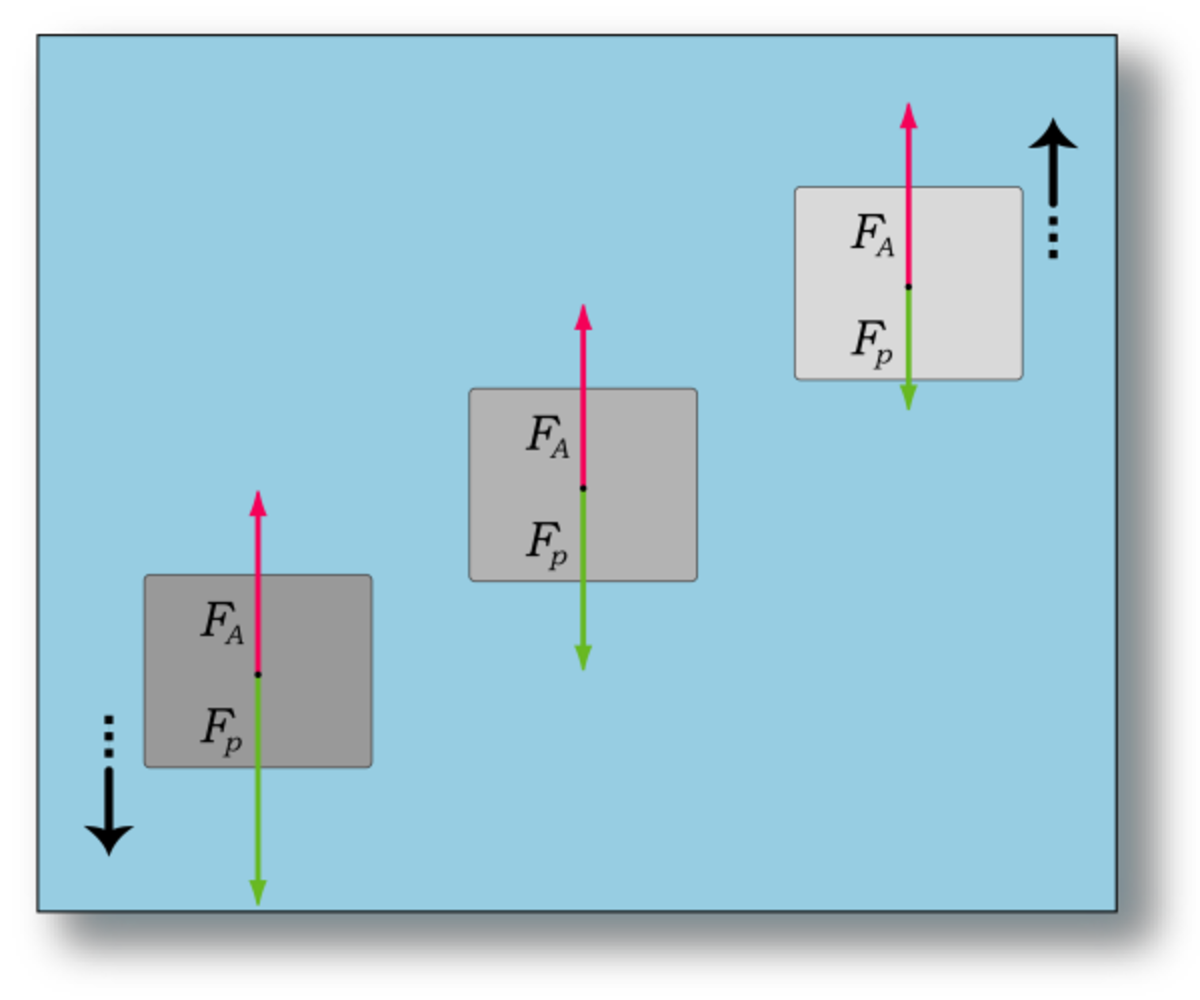
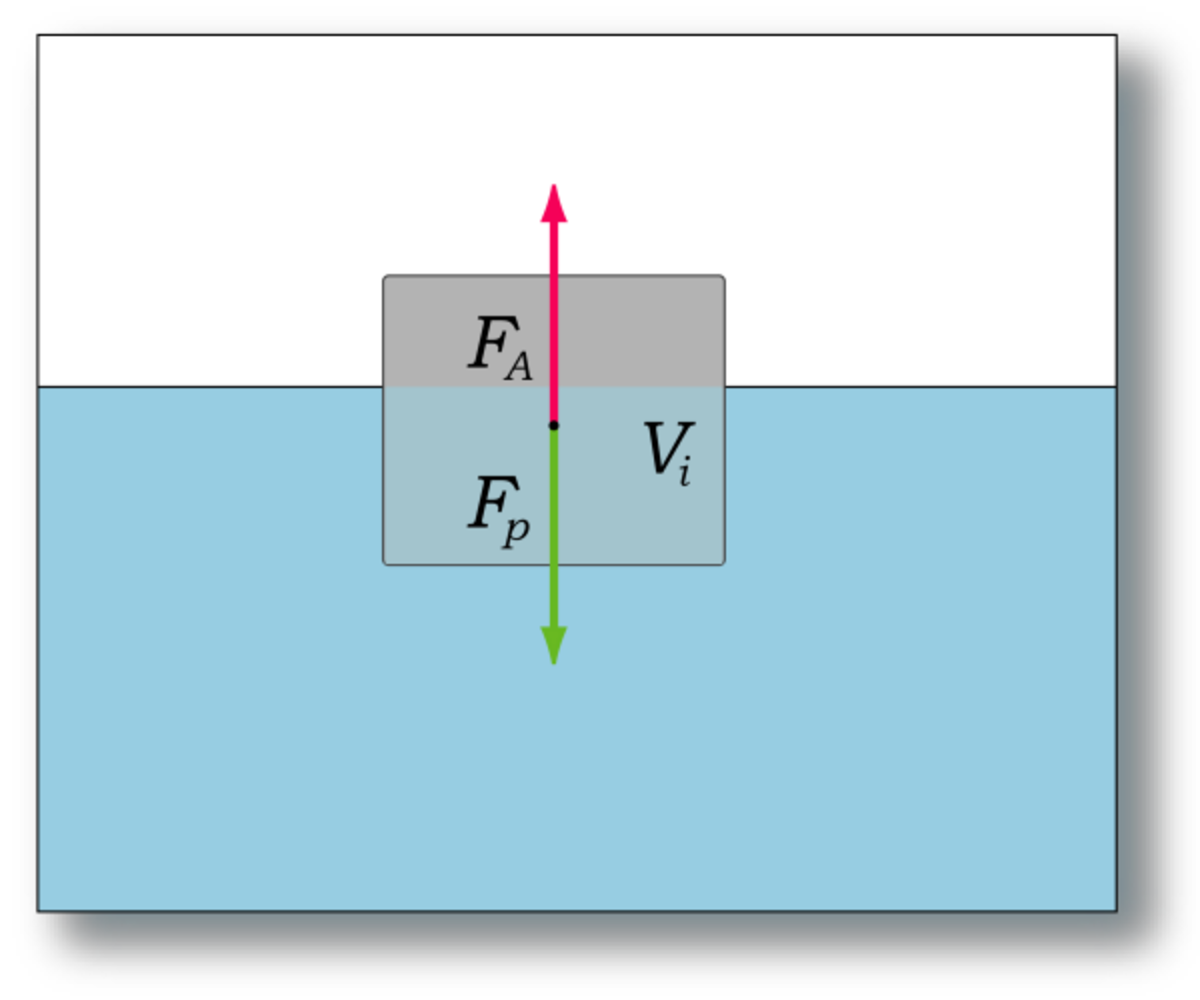
Immergeons entièrement un solide de volume V, de masse m et de masse volumique ρ dans un fluide de masse volumique ρ uniforme, puis relâchons-le à partir du repos. Au départ, la vitesse étant nulle, deux forces seulement agissent sur le solide : son poids F (vers le bas) et la poussée d'Archimède F (vers le haut).

F = ρV g

F = ρV g

F / F = ρ / ρ

Le rapport des masses volumiques est en l'occurrence équivalent à celui des densités.

• Si la densité du solide est supérieure à celle du fluide, alors F > F et le solide coule.
• Si la densité du solide est égale à celle du fluide, alors F = F et le solide demeure immobile ; il est en équilibre neutre ou indifférent.
• Si la densité du solide est inférieure à celle du fluide, alors F < F et le solide remonte vers la surface.

Dans les deux cas où le solide n'est pas en équilibre, son mouvement ultérieur est déterminé par trois forces : son poids, la poussée d'Archimède (opposée au poids) et une force de frottement visqueux F (opposée à la vitesse).

Selon la deuxième loi du mouvement de Newton, on a alors :

F – F ± F = m a (le sens positif est vers le bas)

où a est l'accélération du solide.

Comme la force de frottement visqueux n'est pas constante, mais qu'elle augmente avec la vitesse, l'accélération diminue graduellement, de sorte que le solide atteint plus ou moins rapidement une vitesse limite, lorsque la résultante des forces est nulle.

Exemple d'un solide flottant à la surface d'un liquide

La poussée d'Archimède équilibre le poids du solide.
En réalité, le point d'application de la poussée d'Archimède devrait se trouver au centre du volume immergé, donc plus bas que le centre de gravité du solide.

Considérons un solide de volume V et de masse volumique ρ flottant à la surface d'un liquide de masse volumique ρ. Si le solide flotte, c'est que son poids est équilibré par la poussée d'Archimède :

F = F .

La poussée d'Archimède étant égale (en grandeur) au poids du volume de liquide déplacé (équivalent au volume V immergé), on peut écrire :

ρV g = ρV g .

Le volume immergé vaut donc

V = ( ρ / ρ ) V .

Puisque V > V, il s'ensuit que ρ < ρ .

Application au cas d'un iceberg

Considérons un morceau de glace pure à 0 °C flottant dans de l'eau de mer. Soit ρ = 0,917 kg/dm³ et ρ = 1,025 kg/dm³ (on aurait ρ = 1,000 kg/dm³ pour de l'eau pure à 3,98 °C). Le rapport ρ / ρ (c’est-à-dire la densité relative) est de 0,895, si bien que le volume immergé V représente près de 90% du volume total V de l'iceberg.

Un glaçon qui fond dans un verre

Le volume de glace immergée correspond au volume d'eau produit par la fonte du glaçon.

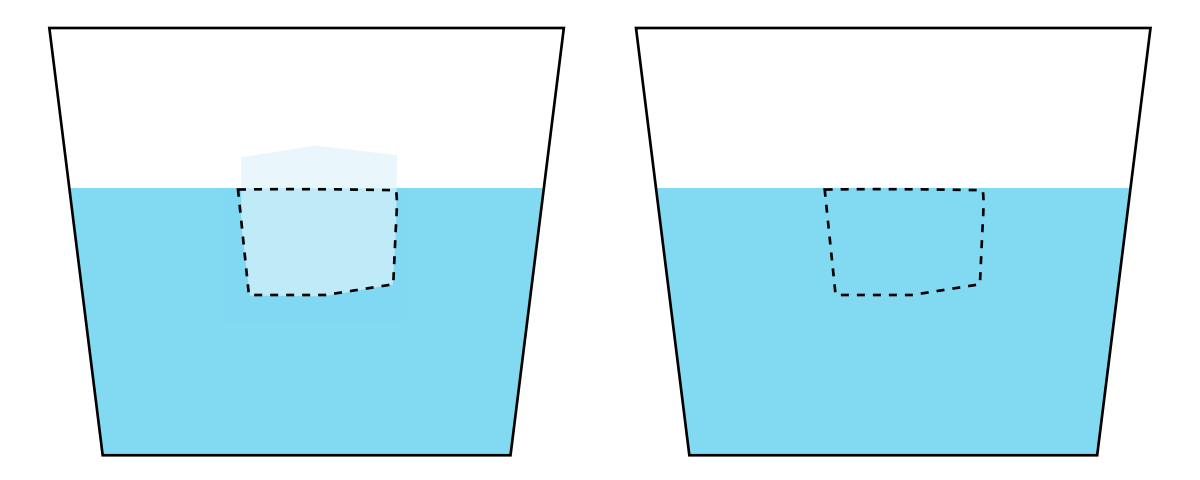
Il est facile de vérifier que la fonte d'un morceau de glace pure flottant sur de l'eau pure se produit sans changement de niveau de l'eau. Le volume de glace immergé correspond en effet au volume d'eau liquide nécessaire pour égaler le poids du glaçon. En fondant, le glaçon produit (par conservation de la masse) exactement ce volume d'eau, qui « bouche le trou laissé par la disparition de la glace solide ». Le niveau d'eau reste le même. Sur la figure ci-contre, le volume délimité en pointillé est, dans le verre de gauche, le volume de glace immergée, et dans le verre de droite, le volume d'eau liquide produit par la fonte du glaçon.

On peut également faire le calcul suivant : si on considère, par exemple, un glaçon de 1 cm³ et de masse volumique 0,917 g·cm^-3 (qui contient donc 0,917 g d'eau), le volume immergé sera de 0,917 cm³ (comme pour un iceberg, la majeure partie est sous l'eau). Lorsque le glaçon aura fondu, ces 0,917 g d'eau qui auront désormais une masse volumique de 1 g·cm^-3 occuperont exactement le volume qu'occupait la partie immergée du glaçon.

Autres exemples d'application de la poussée d'Archimède

La salinité de la mer Morte permet à une personne de flotter tout en étant couchée.

• Le principe d'Archimède s'applique à des fluides, c’est-à-dire aussi bien à des liquides qu'à des gaz. C'est ainsi grâce à la poussée d'Archimède qu'une montgolfière ou un dirigeable peuvent s'élever dans les airs (dans les deux cas, un gaz de masse volumique plus faible que l'air est utilisé, que ce soit de l'air chauffé ou de l'hélium).
• Un plongeur se met à « couler » vers -12 m dans l'Atlantique ou la Méditerranée car sa densité augmente avec la profondeur (à cause de la compression croissante, particulièrement des bulles contenues dans le néoprène de sa combinaison : sa masse ne change pas mais son volume diminue) jusqu'à atteindre et dépasser celle du milieu ambiant.
• L'eau douce ayant une masse volumique plus faible que l'eau salée, la poussée d'Archimède est plus forte dans la mer Morte (mer la plus salée du monde) que dans un lac. Il est donc plus facile d'y flotter.
• Les spationautes s'entraînent aux exercices dans l'espace dans des piscines où, grâce à la poussée d'Archimède qui équilibre leur poids, ils peuvent connaître un état qui s'apparente jusqu'à un certain point à l'impesanteur.
• Le poids des navires (et donc leur masse volumique) variant suivant qu'ils soient en charge ou sur lest, la poussée d'Archimède va également varier. Pour maintenir un niveau de flottaison (tirant d'eau) constant et assurer une meilleure stabilité, les navires sont pourvus de ballasts qu'ils peuvent remplir ou vider suivant leur cargaison ou la salinité de l'eau dans laquelle ils naviguent.(Voir aussi carène).
• Les sous-marins contrôlent leur masse volumique en utilisant également des ballasts.
• Le ludion.
• L'hydromètre qui permet la mesure de la masse volumique d'un liquide.

Point d'application

Tout se passe comme si la poussée d'Archimède s'appliquait au centre de carène, c'est-à-dire au centre de gravité du volume de fluide déplacé.

Cette caractéristique est importante pour le calcul de la stabilité d'un sous-marin en plongée ou d'un aérostat : sous peine de voir l'engin se retourner, il est nécessaire que le centre de carène soit situé au-dessus du centre de gravité.

Pour ce qui est d'un navire, en revanche, le centre de carène est souvent situé au-dessous du centre de gravité (par exemple pour une planche à voile). Cependant, lorsque la pénétration de l'objet dans le fluide évolue, le centre de carène se déplace, créant un couple qui vient s'opposer au mouvement. La stabilité est alors assurée par la position du métacentre, qui est le point d'application des variations de la poussée. Ce métacentre doit se trouver au-dessus du centre de gravité.

De façon anecdotique, on peut remarquer que les concepteurs de sous-marins doivent s'assurer simultanément de deux types d'équilibres pour leurs engins.