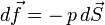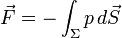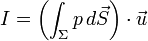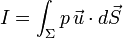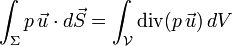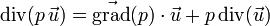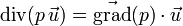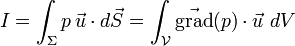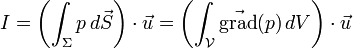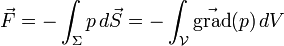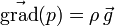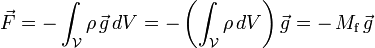Poussée d'Archimède - Définition

Démonstration

Expérience de pensée

Considérons un fluide au repos. Délimitons, par une expérience de pensée, un certain volume de forme quelconque au sein de ce fluide. Ce volume est lui aussi au repos : malgré son poids, ce volume ne tombe pas. Cela signifie donc que son poids est rigoureusement équilibré par une force opposée, qui le maintient sur place, et qui provient du fluide extérieur. Remplaçons maintenant, toujours dans notre expérience de pensée, ce volume par un corps quelconque. Comme la force qui maintenait le fluide en équilibre est une force de pression agissant à la surface du volume, il est possible de supposer que cette même force s'applique encore au corps immergé  : elle est toujours opposée au poids de fluide déplacé. C'est la poussée d'Archimède. Le fait que les champs de force soient identiques pour le fluide homogène au repos et pour le corps immergé dans le fluide au repos est appelé « théorème de solidification ».

Idée de calcul

Supposons un cube d'arête a entièrement immergé dans un liquide, sa face du haut étant horizontale et située à une profondeur z > 0 (le sens positif est vers le bas).

Dans le cas d'un liquide incompressible au repos soumis à un champ de pesanteur uniforme, la pression absolue p vaut

p = p + p ,

où p est la pression atmosphérique et p la pression hydrostatique.

À une profondeur z, la pression hydrostatique correspond au poids P d'une colonne de liquide (que l'on peut imaginer cylindrique) de hauteur z et de base A, divisé par la base. Or

P = m g = [ρ (z A)] g ,

où m est la masse de la colonne, zA son volume, ρ la masse volumique (supposée uniforme) du liquide et g l'accélération de la gravité, ce qui donne

p = P / A = ρ g z .

La pression absolue vaut donc

p = p + ρ g z .

Par symétrie, les forces de pression exercées sur les quatre faces verticales du cube s'annulent deux à deux.

La force F exercée vers le bas sur la face du haut, d'aire A = a², vaut

F = p A = (p + ρ g z) a ².

La force F exercée vers le haut sur la face du bas, située à la profondeur z = z + a, vaut

F = pA = (p + ρ g z) a² = [p + ρ g (z + a)] a².

La résultante F de toutes les forces de pression vaut donc

F = F – F = – (ρ g a) a² = – ρ g a³ = – ρ g V = – ρV g = – Mg ,

où V = a³ est le volume du cube, c'est-à-dire en l'occurrence le volume immergé, et M la masse du fluide contenu dans un volume V. La grandeur de la force résultante est donc bien égale à celle du poids Mg du volume de fluide déplacé ; cette force étant négative, elle est bien orientée verticalement vers le haut.

Il est possible de généraliser la démonstration précédente à un volume de forme quelconque. Il suffit de décomposer la surface bordant le volume en une infinité d'éléments infinitésimaux dS supposés plans, puis de faire la somme, à l'aide du calcul intégral, de toutes les forces infinitésimales df exercées sur chaque élément de surface.

Démonstration plus générale

Supposons un volume quelconque , délimité par une surface fermée , plongé entièrement dans un fluide de masse volumique soumis à un champ de pesanteur uniforme .

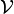
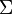
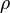
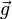
On cherche à déterminer la résultante des forces de pression exercées sur le volume :

.

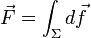
Par définition de la pression , on a

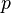
où est un élément infinitésimal de la surface considérée, orienté par convention vers l'extérieur de cette surface, et l'élément infinitésimal de force qui s'y exerce. On cherche donc à déterminer

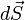
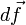
Pour les besoins de la démonstration, considérons maintenant l'intégrale suivante, où l'on supposera que représente un champ de vecteurs uniforme et non nul :

étant uniforme, on peut aussi bien écrire

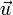
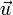
Selon le théorème de flux-divergence,

Or, d'après l'une des formules de Leibniz de l'analyse vectorielle,

Et puisque la divergence d'un champ de vecteurs uniforme est nulle, on a

Par conséquent,

étant uniforme, on peut aussi bien écrire :

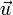
On en déduit donc que

Or, d'après la loi fondamentale de l'hydrostatique,

D'où

La résultante des forces de pression est donc égale en grandeur au poids du volume de fluide déplacé, mais orientée dans le sens contraire du poids, c'est-à-dire vers le haut.