Potentiel vecteur du champ magnétique - Définition

Calcul du potentiel vecteur

En magnétostatique, la loi de Biot et Savart donne l'expression du champ magnétique en fonction des courants électrique présent :

.

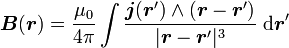
Par ailleurs on sait que, vis-à-vis d'une région centrée autour du rayon vecteur r, on a :

.

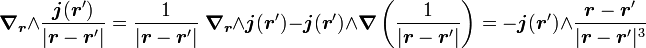
En utilisant cette relation le champ magnétique peut se réexprimer sous la forme :

.

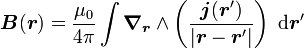
Dans cette formule, on peut sortir le rotationnel de l'intégrale, puisque celui-ci s'applique au rayon vecteur r, d'où

.

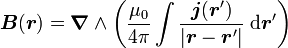
D'après la définition du potentiel vecteur, on en déduit finalement que

,

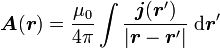
une formule essentiellement identique à celle du potentiel électrique si l'on remplace les charges par les courants.