Potentiel hydrogène - Définition

Mesure et indicateurs

Rouleau de papier pH

L’activité d’un ion n’étant pas directement mesurable, on mesure la force électromotrice engendrée par une différence de pH, d’où l’utilisation d’une référence. Cette relation suit la loi de Nernst :

dans laquelle X est la solution dont le pH est inconnu et S, la solution de référence ; avec ln(10).R.T.F^-1 = 59 159 mV à 298 K (R est la constante des gaz parfaits, T, la température et F, la constante de Faraday).

Généralement, le pH est mesuré par électrochimie avec un pH-mètre, appareil comportant une électrode combinée spéciale, dite électrode de verre, ou deux électrodes séparées. L’électrode de référence est en général au calomel saturé ().

Il existe de nombreuses façons de mesurer l’acidité, on utilise fréquemment des indicateurs de pH.

Activité et concentration

Pour des concentrations ioniques importantes, l’activité ne peut plus être assimilée à la concentration et on doit tenir compte de la force ionique, par exemple grâce à la théorie de Debye-Hückel. Le pH d’une solution décamolaire d’acide fort n’est donc pas égal à -1 comme le pH d’une solution décamolaire de base forte n’est pas égal à 15. L’agressivité de telles solutions et leur force ionique importante rend la mesure du pH délicate avec les habituelles électrodes de verre. On a donc recours à d’autres méthodes s’appuyant sur les indicateurs colorés (spectroscopie ou ). Pour des concentrations élevées de H⁺, on peut définir par analogie d’autres échelles de mesure d’acidité, telle l’échelle de Hammett H.

pH négatif

En conséquence des formules précédentes, lorsque la concentration est supérieure à 1, ce qui n’a rien d’impossible, le pH devient négatif.

Dans des solutions assez peu concentrées (on dit « solution diluée »), l’acidité est mesurée par la concentration en ions hydronium (oxonium) ou [H₃O⁺], car les ions H⁺ s’associent avec [H₂O]. Cependant, aux fortes concentrations, cet effet est en partie contrebalancé par les coefficients d’activité qui s’effondrent aux concentrations élevées. Néanmoins, il est possible d’obtenir des pH négatifs.

Par exemple, les laboratoires peuvent se procurer un acide chlorydrique [HCl] concentré commercial (37 % en masse) qui fournit un pH d’environ -1,1 ; de même, une solution saturée en NaOH a un pH de 15,0.

Les produits plus acides que l’acide sulfurique à 100 %, sont qualifiés de superacides. Ceux-ci sont couramment utilisés, notamment comme catalyseurs pour l’isomérisation et le craquage des alcanes.

Formules de calcul approché du pH pour des solutions aqueuses

a 25 °C pK_e = 14

Cas d'un acide fort

où C_a est la concentration en acide en mol/L

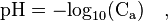
Cette relation n’est pas valable pour des concentrations inférieures à 1×10^-7 mol⋅L^-1 et ne devrait s’appliquer qu’avec des concentrations supérieures à 1×10^-5 mol⋅L^-1. Son application à une solution diluée à 10^-8 donne en effet pH = 8, ce qui est absurde puisque la solution est acide et non alcaline (le pH d’une telle solution est de 6,98) ;

Dans le cas d’un monoacide, le pH se calcule en résolvant l’équation du troisième degré suivante : (H⁺)³ + K (H⁺)² - (H⁺) [K + K C] - K.K = 0 ;

Dans le cas limite , l’équation précédente devient alors (H ⁺ )² − C_aH ⁺ − K_e = 0 d’où on déduit que . Lorsque , on a .

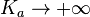
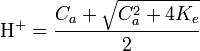
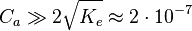
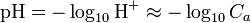
Cas d'une base forte

où C_b est la concentration en base en mol.L^-1.

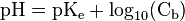
Cette relation est soumise aux mêmes remarques que pour le cas d’un acide fort.

Cas d'un acide faible

où le pK_a est celui de l’acide.

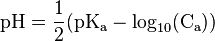
Cas d'une base faible

où le pK_a est celui de l’acide créé.

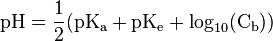
Cas d'un mélange de solutions de pH connus

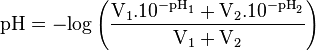
Cette formule est très approximative, notamment si les acides ou bases utilisés sont faibles, et devrait être utilisée avec la plus grande prudence.