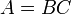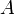Polynôme - Définition
La liste des auteurs de cet article est disponible ici.
Divisibilité
En algèbre commutative, c'est-à-dire dans un anneau commutatif unitaire intègre, une attention particulière est portée sur l'étude de la divisibilité entre les polynômes. Des résultats plus forts existent quand les coefficients sont pris dans un corps.
Coefficients dans un anneau commutatif unitaire intègre
Si f et g sont des polynômes dans A[X], nous dirons que f divise g s'il existe un polynôme q dans A[X] tel que f.q = g.
On peut démontrer alors que « chaque racine engendre un facteur linéaire », ou plus formellement que : si f est un polynôme dans A[X] et a est un élément de A tel que f ( a ) = 0, alors le polynôme ( X - a ) divise f. La réciproque est aussi vraie. Le quotient peut être calculé en utilisant la méthode de Horner.
Certains polynômes aux propriétés particulières se détachent alors :
- Polynôme inversible : un polynôme P est inversible s'il existe un polynôme Q tel que P.Q = 1.
-
- Les seuls polynômes inversibles de A[X] sont les polynômes constants dont la constante est inversible dans A.
- Polynôme irréductible : P est un polynôme irréductible s'il n'est ni nul, ni inversible, ni produit de deux polynômes non inversibles.
-
- Un polynôme du premier degré aX+b est donc irréductible si et seulement si a et b sont premiers entre eux (par exemple, tout polynôme unitaire du premier degré est irréductible, tandis que 2X+2=2(X+1) n'est pas irréductible dans
![\mathbb Z[ X ]\,](https://static.techno-science.net/illustration/Definitions/autres/a/aeda3a650f5a801a6d09dbc8e9fc2a64_7d479593eb81d62de96803fa3aff7dd3.png)
- Le polynôme X 2 + 1 est irréductible dans
![\mathbb R[ X ] \,](https://static.techno-science.net/illustration/Definitions/autres/b/b54e84099d870bd11192e90017d3226c_715e0f05faf915aeda60b802ddca0029.png)
![\mathbb C [ X ] \,](https://static.techno-science.net/illustration/Definitions/autres/2/2026f1a6452ae3da0c3e2c14b049623f_df76c369b8fb9ab2275b565cc34f0a20.png)
- Si A est un anneau factoriel, alors tout polynôme se décompose de manière unique, à un inversible près, en produit de polynômes irréductibles. A[X] est donc aussi factoriel.
- Un polynôme du premier degré aX+b est donc irréductible si et seulement si a et b sont premiers entre eux (par exemple, tout polynôme unitaire du premier degré est irréductible, tandis que 2X+2=2(X+1) n'est pas irréductible dans
- Polynôme premier : P est un polynôme premier s'il n'est ni nul ni inversible et si, pour tout produit Q.S divisible par P, l'un des deux polynômes Q ou S est divisible par P.
-
- Dans le cas où A est factoriel, les notions de polynôme premier et polynôme irréductible sont équivalentes mais, dans les autres cas, on a seulement la propriété suivante : un polynôme premier est irréductible.
- Polynôme primitif : Si A est un anneau factoriel, P est un polynôme primitif si le pgcd de ses coefficients est inversible.
Dans un anneau commutatif unitaire, un polynôme est dit primitif lorsque l'anneau est le plus petit idéal principal contenant les coefficients du polynôme.
- Polynôme scindé : Un polynôme scindé est un polynôme qui peut s'écrire comme produit de polynômes du premier degré.
-
- X 2 + 1 est scindé sur
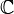
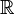
- X 2 + 1 est scindé sur
- Polynôme séparable: Polynôme qui peut s'écrire dans un sur-anneau intègre de A comme produit de polynômes du premier degré X - a i où tous les a i sont distincts.
- Polynômes premiers entre eux : P et Q sont premiers entre eux si les seuls polynômes qui divisent à la fois P et Q sont les polynômes inversibles.
- Polynôme unitaire : Polynôme dont le coefficient du terme de plus haut degré est 1.
- Polynôme cyclotomique : pour
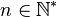
Coefficients dans un corps commutatif
Si K est un corps et f et g sont des polynômes dans K[X] avec g ≠ 0, alors il existe des polynômes q et r dans K[X] avec : f = q g + r et tels que le degré de r soit strictement plus petit que le degré de g. Les polynômes q et r sont uniquement déterminés par f et g. C'est ce que l'on appelle la division euclidienne ou «la division suivant les puissances décroissantes» de f par g et cela montre que l'anneau K[X] est un anneau euclidien.
K[X] est donc un anneau euclidien (seul les anneaux de polynômes à coefficients dans un corps sont des anneaux euclidiens) et cela permet alors de définir les notions de ppcm, de pgcd avec la mise en place d'un algorithme d'Euclide de recherche de pgcd. On retrouve aussi l' identité de Bézout sur les polynômes premiers entre eux : si P et Q sont premiers entre eux, il existe deux polynômes U et V tels que UP + VQ = 1 .
Réductibilité des polynômes de ℤ[X]
Un polynôme primitif A de
![\mathbb{Z}[X]](https://static.techno-science.net/illustration/Definitions/autres/8/8948f9796109cbb4f99d4dd5ba0b3b82_f550541c17eb429ba1b0618ba09d0a1b.png)
![\mathbb{Q}[X]](https://static.techno-science.net/illustration/Definitions/autres/1/12e7b267ca89f819cb51e1e108ba6678_7e83301ef2e1116ad54ff923cbb6e2f9.png)
![\mathbb{Q}[X]](https://static.techno-science.net/illustration/Definitions/autres/1/12e7b267ca89f819cb51e1e108ba6678_7e83301ef2e1116ad54ff923cbb6e2f9.png)
![\mathbb{Q}[X]](https://static.techno-science.net/illustration/Definitions/autres/1/12e7b267ca89f819cb51e1e108ba6678_7e83301ef2e1116ad54ff923cbb6e2f9.png)
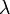
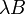
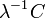
![\mathbb{Z}[X]](https://static.techno-science.net/illustration/Definitions/autres/8/8948f9796109cbb4f99d4dd5ba0b3b82_f550541c17eb429ba1b0618ba09d0a1b.png)
Indications sur la démonstration:
- Tout d'abord définissons l'application
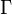
![\mathbb{Z} [X]](https://static.techno-science.net/illustration/Definitions/autres/8/8948f9796109cbb4f99d4dd5ba0b3b82_f550541c17eb429ba1b0618ba09d0a1b.png)
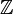
![\quad A[X] = \sum_{k=0}^n a_k X^{n-k} , \qquad \quad\Gamma (A) = \operatorname{pgcd}(a_0, a_1, ..., a_n)](https://static.techno-science.net/illustration/Definitions/autres/f/fb9342766a953d2cf4d4300c646ae9cc_8939d0f844baba8f292bddbdcff04f3c.png)
On vérifiera que pour tous
![\quad A, B \in\mathbb Z[X]](https://static.techno-science.net/illustration/Definitions/autres/3/3c28d2ba3ee67865feac9a02f493cb93_8ae19fde46071b20b9b43f649070fa97.png)
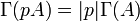
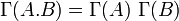
- Supposons alors que
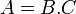
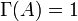
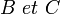
![\mathbb Q [X]](https://static.techno-science.net/illustration/Definitions/autres/9/9918bced8e53444100ccab7a8a59f47d_2cec35570b28ace18388d52b9029d78c.png)
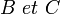
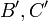
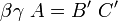
Mais
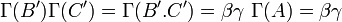
En posant
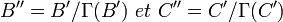
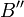
![\quad C''\in\mathbb Z [X]](https://static.techno-science.net/illustration/Definitions/autres/9/921e993cdda2be0ba007bde6564e6c9b_f3e9ca07a33c90254378fb5306a7123a.png)
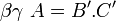
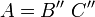
- Le cas général où l'on n'a plus nécessairement
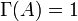
- Remarque
Si
![\quad A, B, C \in \mathbb Z [X]](https://static.techno-science.net/illustration/Definitions/autres/5/5a59beefb74d4f7ed300a641930960ed_a0664c6624727f6e05000f658ddb34bd.png)