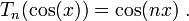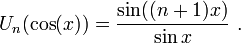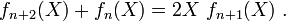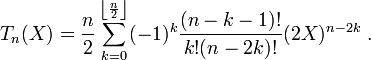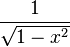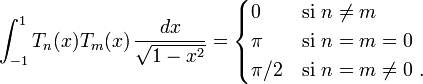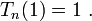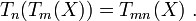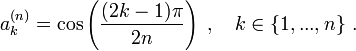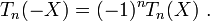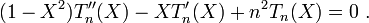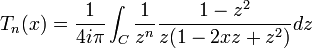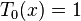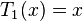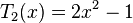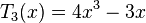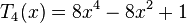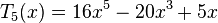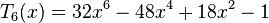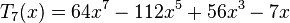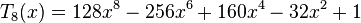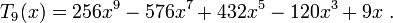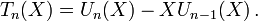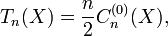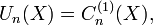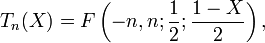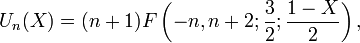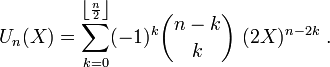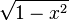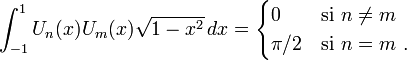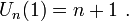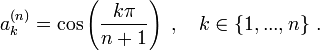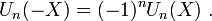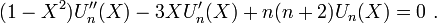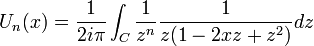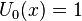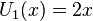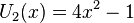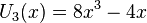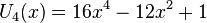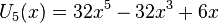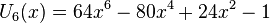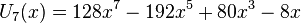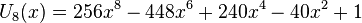Samedi 26 Avril 2025
Rechercher 🔍

Polynôme de Tchebychev - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Propriétés des polynômes de Tchebychev de 1re espèce - Quelques relations avec d'autres fonctions spéciales - Propriétés des polynômes de Tchebychev de 2e espèce - Bibliographie - Intérêt

Introduction

Les polynômes de Tchebychev sont nommés d'après le mathématicien Pafnouti Tchebychev. Ils forment deux familles de polynômes, indexés par leur degré.

Le polynôme de Tchebychev de première espèce Tn est défini par la propriété suivante : pour tout nombre réel x,

T_{n}(\cos(x))=\cos(nx)~.

Le polynôme de Tchebychev de seconde espèce Un est défini par :

U_{n}(\cos(x))=\frac{\sin((n+1) x)}{\sin x}~.

Chacune de ces deux suites forme une famille de polynômes orthogonaux par rapport à une certaine fonction poids, et vérifie la relation de récurrence suivante :

f_{n+2}(X)+f_{n}(X)=2X\ f_{n+1}(X)~.

Propriétés des polynômes de Tchebychev de 1re espèce

  • Pour tout entier n strictement positif,
T_n(X)=\frac{n}{2}\sum_{k=0}^{\left\lfloor \frac{n}2\right\rfloor}(-1)^k \frac{(n-k-1)!}{k!(n-2k)!}(2X)^{n-2k}~.
  • Les Tn sont orthogonaux pour le poids
\frac{1}{\sqrt{1-x^2}}

sur l'intervalle ]−1,1[, et on sait calculer leur norme. Plus précisément,

\int_{-1}^1 T_n(x)T_m(x)\,\frac{dx}{\sqrt{1-x^2}}= \begin{cases} 0&\text{si}~n\ne m\\ \pi&\text{si}~n=m=0\\ \pi/2&\text{si}~n=m\ne 0~. \end{cases}
T_n(1)=1~.
  • Quels que soient les entiers naturels m et n,
T_n(T_m(X))=T_{mn}(X)~.
  • Pour tout entier n strictement positif, le coefficient dominant de Tn est 2n-1 et ses n racines sont
a_k^{(n)}=\cos\left(\frac{(2k-1)\pi}{2n}\right)\;,\quad k\in\{1,...,n\}~.
  • La parité dépend de n :
T_{n}(-X)=(-1)^nT_{n}(X)~.
  • Ils vérifient l'équation différentielle suivante :
(1-X^2)T_{n}''(X)-XT_n'(X)+n^2T_n(X)=0~.
  • Représentation intégrale :
T_n(x)=\frac{1}{4i\pi}\int_C\frac{1}{z^n}\frac{1-z^2}{z(1-2xz+z^2)}dz

avec C un contour dans plan complexe autour de zéro, dans le sens positif, les zéros de z − 2xz + z2 étant en dehors de C.

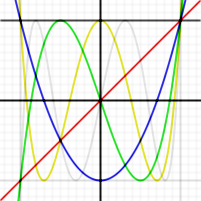
Les premiers polynômes de Tchebychev de première espèce sur le domaine −1¼ < x < 1¼, −1¼ < y < 1¼; la fonction constante T0, et T1, T2, T3, T4 et T5.

Les premiers polynômes de Tchebychev de première espèce sont :

T_0(x) = 1 \,
T_1(x) = x \,
T_2(x) = 2x^2 - 1 \,
T_3(x) = 4x^3 - 3x \,
T_4(x) = 8x^4 - 8x^2 + 1 \,
T_5(x) = 16x^5 - 20x^3 + 5x \,
T_6(x) = 32x^6 - 48x^4 + 18x^2 - 1 \,
T_7(x) = 64x^7 - 112x^5 + 56x^3 - 7x \,
T_8(x) = 128x^8 - 256x^6 + 160x^4 - 32x^2 + 1 \,
T_9(x) = 256x^9 - 576x^7 + 432x^5 - 120x^3 + 9x~.

Quelques relations avec d'autres fonctions spéciales

T_n(X)=U_n(X)-X U_{n-1}(X)\,.
T_n(X)=\frac{n}2C_{n}^{(0)}(X),
U_n(X)=C_{n}^{(1)}(X),

avec C_n^{(k)} un polynôme de Gegenbauer et

T_{n}(X)=F\left(-n,n;\frac{1}{2};\frac{1-X}{2}\right),
U_{n}(X)=(n+1)F\left(-n,n+2;\frac{3}{2};\frac{1-X}{2}\right),

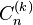
avec F la fonction hypergéométrique.

Propriétés des polynômes de Tchebychev de 2e espèce

  • Pour tout entier n strictement positif,
U_n(X)=\sum_{k=0}^{\left\lfloor \frac{n}2\right \rfloor}(-1)^k \binom{n-k}{k}~(2X)^{n-2k}~.
  • Les Un sont orthogonaux pour le poids
\sqrt{1-x^2}

sur l'intervalle ]−1,1[. Plus précisément,

\int_{-1}^1 U_n(x)U_m(x)\sqrt{1-x^2}\,dx = \begin{cases} 0&\text{si}~n\ne m\\ \pi/2 &\text{si}~n=m~. \end{cases}
  • Pour tout entier naturel n,
U_{n}(1) = n+1~.
  • Pour tout entier n strictement positif, les n racines de Un sont
a_k^{(n)}=\cos\left(\frac{k\pi}{n+1}\right)\;,\quad k\in\{1,...,n\}~.
  • La parité dépend de n :
U_n(-X)=(-1)^nU_n(X)~.
  • Ils vérifient l'équation différentielle suivante :
(1-X^2)U_n''(X)-3XU_n'(X)+n(n+2)U_n(X)=0~.
  • Représentation intégrale :
U_n(x)=\frac1{2i\pi}\int_C\frac1{z^n}\frac1{z(1-2xz+z^2)}dz

avec C un contour dans plan complexe autour de zéro, dans le sens positif, les zéros de z − 2xz + z2 étant en dehors de C.

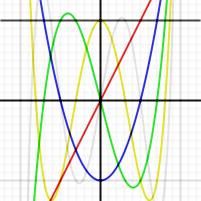
Les premiers polynômes de Tchebychev de seconde espèce sur le domaine −1¼ < x < 1¼, −1¼ < y < 1¼; la fonction constante U0, et U1, U2, U3, U4 et U5.

Les premiers polynômes de Tchebychev de seconde espèce sont :

U_0(x) = 1 \,
U_1(x) = 2x \,
U_2(x) = 4x^2 - 1 \,
U_3(x) = 8x^3 - 4x \,
U_4(x) = 16x^4 - 12x^2 + 1 \,
U_5(x) = 32x^5 - 32x^3 + 6x \,
U_6(x) = 64x^6 - 80x^4 + 24x^2 - 1 \,
U_7(x) = 128x^7 - 192x^5 + 80x^3 - 8x \,
U_8(x) = 256x^8 - 448 x^6 + 240 x^4 - 40 x^2 + 1 \,
U_9(x) = 512x^9 - 1024 x^7 + 672 x^5 - 160 x^3 + 10 x~.

Bibliographie

  • Polynômes de Tchebychev sur Math-Linux.
  • (en) Abramowitz and Stegun, Handbook of Mathematical Functions, chap. 22.

Intérêt

Tchebychev a découvert ceux-ci en travaillant sur le problème de convergence des interpolations de Lagrange. On peut démontrer que pour minimiser l'erreur engendrée par l'interpolation (cf phénomène de Runge), il faut choisir les racines des polynômes de Tchebychev comme points d'interpolation. 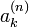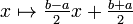Dans ce contexte, ces a_k^{(n)} données ci-dessus, éventuellement ajustés à un autre intervalle d'interpolation [a,b] considéré (par une transformation affine x\mapsto\tfrac{b-a}{2}x+\tfrac{b+a}{2} ), sont appelés les abscisses de Tchebychev.

Les polynômes de Tchebychev sont impliqués dans le calcul de filtres en électronique analogique, les filtres de Tchebychev.

Ils peuvent également servir à démontrer le théorème de Weierstrass (Toute fonction continue sur un intervalle est limite uniforme d'une suite de polynômes).

- Introduction - Propriétés des polynômes de Tchebychev de 1re espèce - Quelques relations avec d'autres fonctions spéciales - Propriétés des polynômes de Tchebychev de 2e espèce - Bibliographie - Intérêt
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
miniature
Comment des impacts géants vaporisent les corps planétaires ☄️
miniature
Les Américains riches vivent moins longtemps que les Européens pauvres 💰
miniature
Attention à ce riz naturellement riche en arsenic 🍚
miniature
L'intelligence artificielle contre la mort subite 💀
miniature
L'inévitable formation d'un océan de magma basal sur Terre 🔥
miniature
Découverte d'une plante étrange sans chlorophylle 🌱
miniature
Existe-t-il des mélodies naturelles ? 🎶
miniature
Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽
miniature
L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡
miniature
1
Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺
miniature
Imprimer en 3D avec la lumière du soleil ☀️
miniature
La pollution atmosphérique nuit gravement au cerveau 🧠
miniature
Le trou noir supermassif Ansky vient de se réveiller ⚫
miniature
1
Voici ce qui rend notre cerveau vraiment unique 🧠
miniature
Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩
miniature
Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬
miniature
La physique révèle les secrets d'un strike parfait au bowling 🎳
miniature
Le TDAH associé à la démence 🧠
miniature
Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️
miniature
Le régime cétogène montre des surprises sur le cholestérol 🧐
miniature
Un tango observationnel révèle une Super-Terre 🔭
miniature
Cette expérience montre que la graisse brune augmente fortement la longévité 🕒
Page générée en 0.119 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise