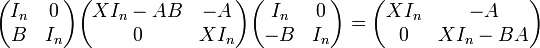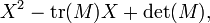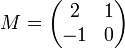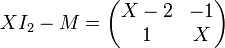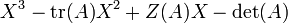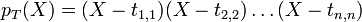Polynôme caractéristique - Définition

Propriétés

• Le polynôme p_M(X) d'une matrice carrée M d'ordre n est unitaire (son coefficient dominant est égal à 1) et son degré est égal à n.

• La matrice M et sa transposée ont le même polynôme caractéristique.

• Le théorème de Cayley-Hamilton affirme qu'en remplaçant X par M dans p_M(X), on obtient la matrice nulle: p_M(M) = 0. Ce qui signifie que le polynôme caractéristique est un polynôme annulateur de M. Par conséquent, il est possible de démontrer que le polynôme minimal divise le polynôme caractéristique de M.

• Deux matrices semblables ont le même polynôme caractéristique. La réciproque n'est pas vraie en général : deux matrices ayant même polynôme caractéristique ne sont pas nécessairement semblables.

• Une matrice M est semblable à une matrice triangulaire si et seulement si son polynôme caractéristique peut être complètement décomposé en produit de facteurs de degré un à coefficients dans . En fait, M est même semblable à une matrice de Jordan dans ce cas.

• Propriété de commutation :

Exemples

• Pour une matrice M d'ordre 2, le polynôme caractéristique s'exprime simplement comme

mais peut aussi se calculer directement à partir de la définition.

Déterminons par exemple le polynôme caractéristique p_M(X) de la matrice

C'est le déterminant de la matrice

On a donc

p_M(X) = (X − 2)(X) − 1( − 1) = X² − 2X + 1.

• Pour une matrice A d'ordre 3, le polynôme caractéristique s'exprime comme

où

,

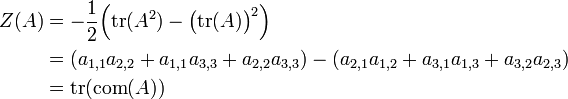
avec a_i,j l'élément en position (i, j) dans la matrice A.

Matrice triangulaire

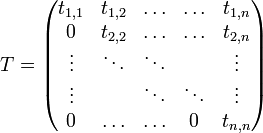
Dans le cas d'une matrice triangulaire (supérieure) d'ordre n, matrice de la forme :

le déterminant p_T(X) = det(XI_n − T) qui exprime le polynôme caractéristique se factorise :

Le même raisonnement s'applique bien sûr au cas d'une matrice triangulaire inférieure. D'une façon générale, les valeurs propres d'une matrice triangulaire coïncident donc effectivement avec ses éléments diagonaux, comme annoncé au .

Matrice compagnon

Soit un polynôme à coefficients dans . La matrice d'ordre n

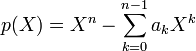
qui admet p(X) comme polynôme caractéristique (et polynôme minimal), est appelée matrice compagnon du polynôme (ou selon certains ouvrages, sa transposée). Une des méthodes utilisées en calcul numérique pour calculer des valeurs approchées des racines d'un polynôme est d'en construire la matrice compagnon puis de calculer des valeurs approchées des valeurs propres de cette matrice à l'aide d'une méthode itérative.