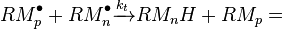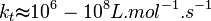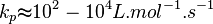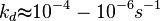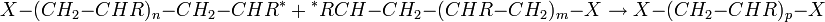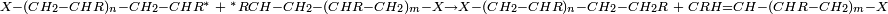Polymérisation radicalaire - Définition
La liste des auteurs de cet article est disponible ici.
Aspect cinétique
| Etape | Réaction | Vitesse associée |
|---|---|---|
| | Etape lente: | |
| Etape rapide: | | |
| | ||
| | | |
| Le temps de demi réaction de la polymérisation:
| ||
| | Recombinaison: | et si AEQS: va = vt alors: |
| Dismutation: | ||
A est l'amorceur qui se décompose en un composé R, M est le monomère.
En général:
Ces valeurs dépendent de la température via la Loi d'Arrhenius et de la longueur de la chaîne.
On peut également introduire la longueur de chaîne cinétique
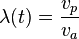
- terminaison par dismutation: DPn = λ
- terminaison par recombinaison: DPn = 2λ
On peut ainsi calculer la concentration en monomère à introduire en fonction du DPn (lié à la masse molaire moyenne) voulu.
Terminaison
Les réactions de terminaison mettent en jeu deux macro-radicaux en croissance.
Dans le premier cas, la réaction de recombinaison, deux macro-radicaux reforment une liaison covalente :
où p = n + m + 2.
Dans le deuxième cas, la réaction de dismutation, les deux macro-radicaux donnent lieu à une réaction de transfert d'hydrogène, suivie d'une recombinaison. Le résultat global peut s'écrire :
La proportion relative de ces deux modes de terminaison dépend essentiellement du type de monomère employé, de l'accessibilité des sites radicalaires c'est-à-dire de l'encombrement stérique des sites actifs.
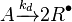
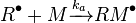
![v_a = k_a[R^ \bullet][M]](https://static.techno-science.net/illustration/Definitions/autres/4/467b0e08d5eb901b528d7a1539e1e5ad_9d7a2932c8d5d958a79d6b95aaf28bbc.png)
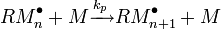
![v_p = -\frac {\mathrm{d}[M]} {\mathrm{d}t} = k_p{\color{Tan}[RM_n^ \bullet]}[M]](https://static.techno-science.net/illustration/Definitions/autres/2/27c1730c6842911eb3d39a8fcf71ce34_b35c94286bafcacc7380039062f78a7e.png)
![\textstyle t_{1/2} = \frac {ln(2)} {k_p{\color{Tan}[RM_n^ \bullet]}}](https://static.techno-science.net/illustration/Definitions/autres/4/4b8091b88bf03c9d4f9e789a9bf331ca_f25eff13f0ca4cb0ed87ba783b1ea458.png)
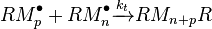
![v_t = 2k_t[RM_n^ \bullet]^2](https://static.techno-science.net/illustration/Definitions/autres/1/1aa0a60cf9c4a66f005e5acc0f2354ee_8647804ab0ba973161abc1b6bd530f6d.png)
![\scriptstyle {\color{Tan}[RM_n^ \bullet]} = \left(\frac{fk_d[A]}{k_t}\right)^{\frac{1}{2}}](https://static.techno-science.net/illustration/Definitions/autres/6/6dab02e331e470568be9089e2b9d6c7b_54c3927c768190a8a0c5245b03bc6ffa.png)