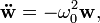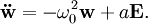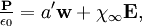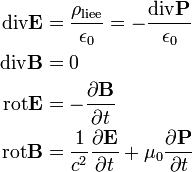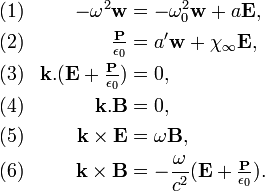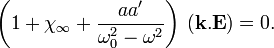Polariton - Définition
La liste des auteurs de cet article est disponible ici.
Polaritons phononiques
Modélisation du couplage entre le champ électromagnétique et les phonons
Pour pousser plus loin l'analogie ci-dessus, on modélise le couplage entre la lumière et les phonons optiques de manière simplifiée, tout en restant dans le cadre de la physique classique. On suppose un cristal infini dont la maille primitive contient deux ions, chargés +/– et bougeant en sens opposé, leur déplacement par rapport à l'équilibre étant représenté par le vecteur
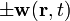
![\mathbf w(\mathbf r, t)=\mathbf w_0 \exp[i(\mathbf{k.r}-\omega t)]](https://static.techno-science.net/illustration/Definitions/autres/8/85ca8d232af4c41874011f8beb6a0475_89f3098971e4796d59413012205a865b.png)
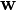
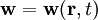
où ω0 est la fréquence des phonons optiques – dans cette équation, le champ w peut être longitudinal ou transverse. Cette équation n'est valable que si l'on néglige le couplage entre les phonons et le champ électromagnétique. Ce dernier agit sur les atomes par une force de Lorentz :
En retour, les ions constituent un dipôle susceptible de rayonner. La polarisation est donnée par
où
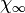
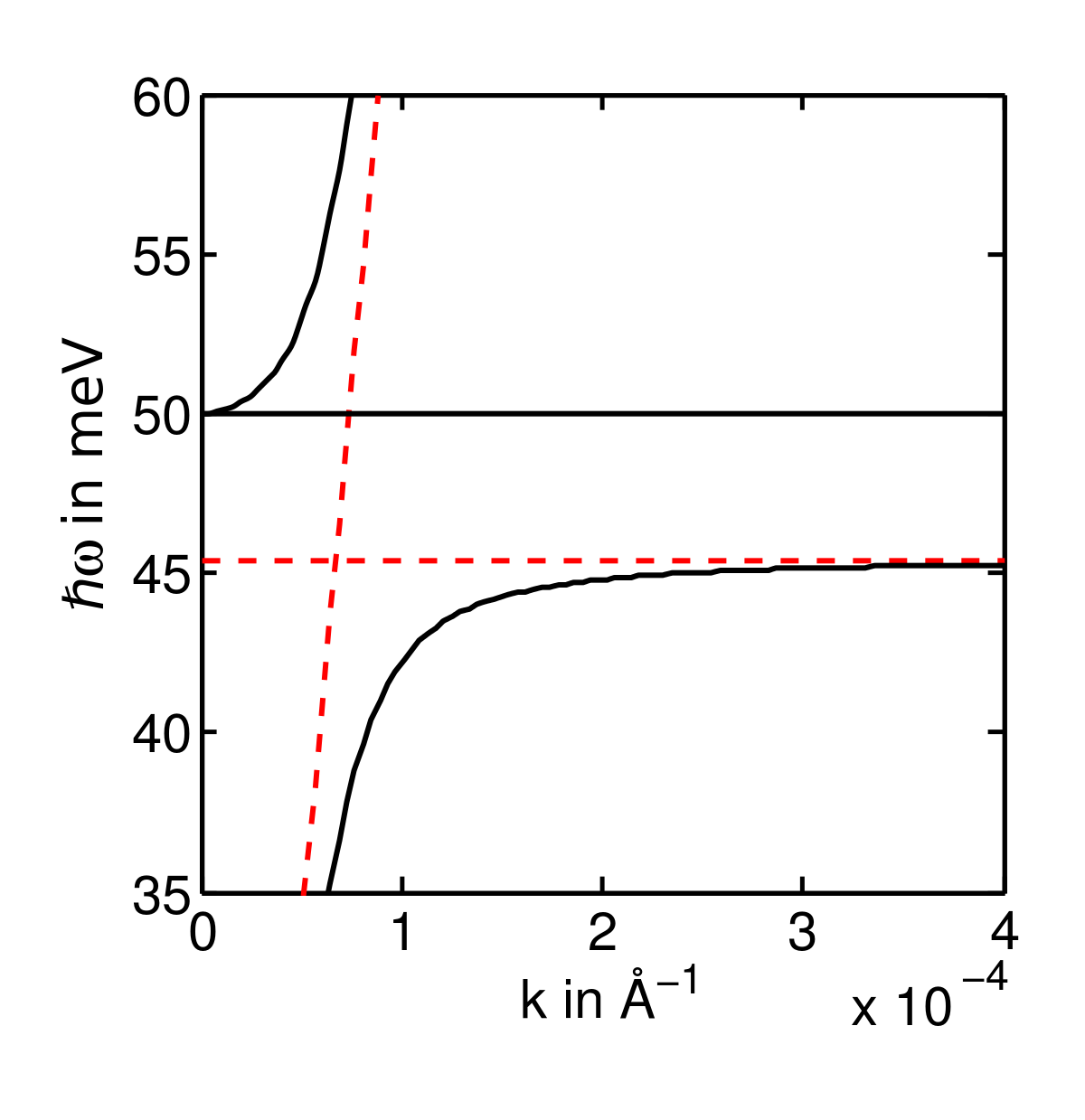
Recherche de modes propres
On obtient donc un système d'équations où la dynamique du champ électromagnétique est couplée à la dynamique du champ de déformation, via les constantes a et a'. On peut donc appliquer la procédure de seconde quantification utilisée en optique quantique pour trouver les photons à partir des champs E et B dans le vide. Cette procédure commence par rechercher les modes propres du système d'équations. On recherche donc des solutions où tous les champs varient comme exp[i(k.r–ωt)]. Les équations deviennent alors
Il n'existe pas de mode propre purement mécanique, car si
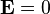
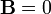
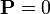
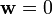
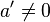
En exprimant
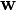
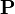
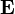
Les deux termes de ce produit peuvent être nuls, ce qui conduit à deux situations possibles :
- des ondes longitudinales où
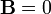
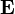
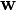
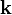
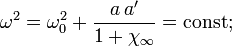
- des ondes transverses où
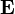
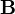
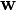
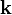
![\mathbf{k}^2 = \frac{\omega^2}{c^2}\left[ 1+\chi_\infty + \frac{a \, a'}{\omega_0^2-\omega^2} \right] .](https://static.techno-science.net/illustration/Definitions/autres/c/c420739f9e294eb44ecb8918d873ef5a_ede89c810504bdb9256886e322d89723.png)