Dimanche 27 Avril 2025
Rechercher 🔍

Point de Lagrange - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Historique - Calcul de la position des points de Lagrange - Définition - Pertinence du concept - Stabilité - Applications

Définition

Un objet de faible masse situé exactement en ces points n'en bouge plus relativement aux deux autres corps, et tourne de concert avec eux (par exemple une planète et le Soleil).

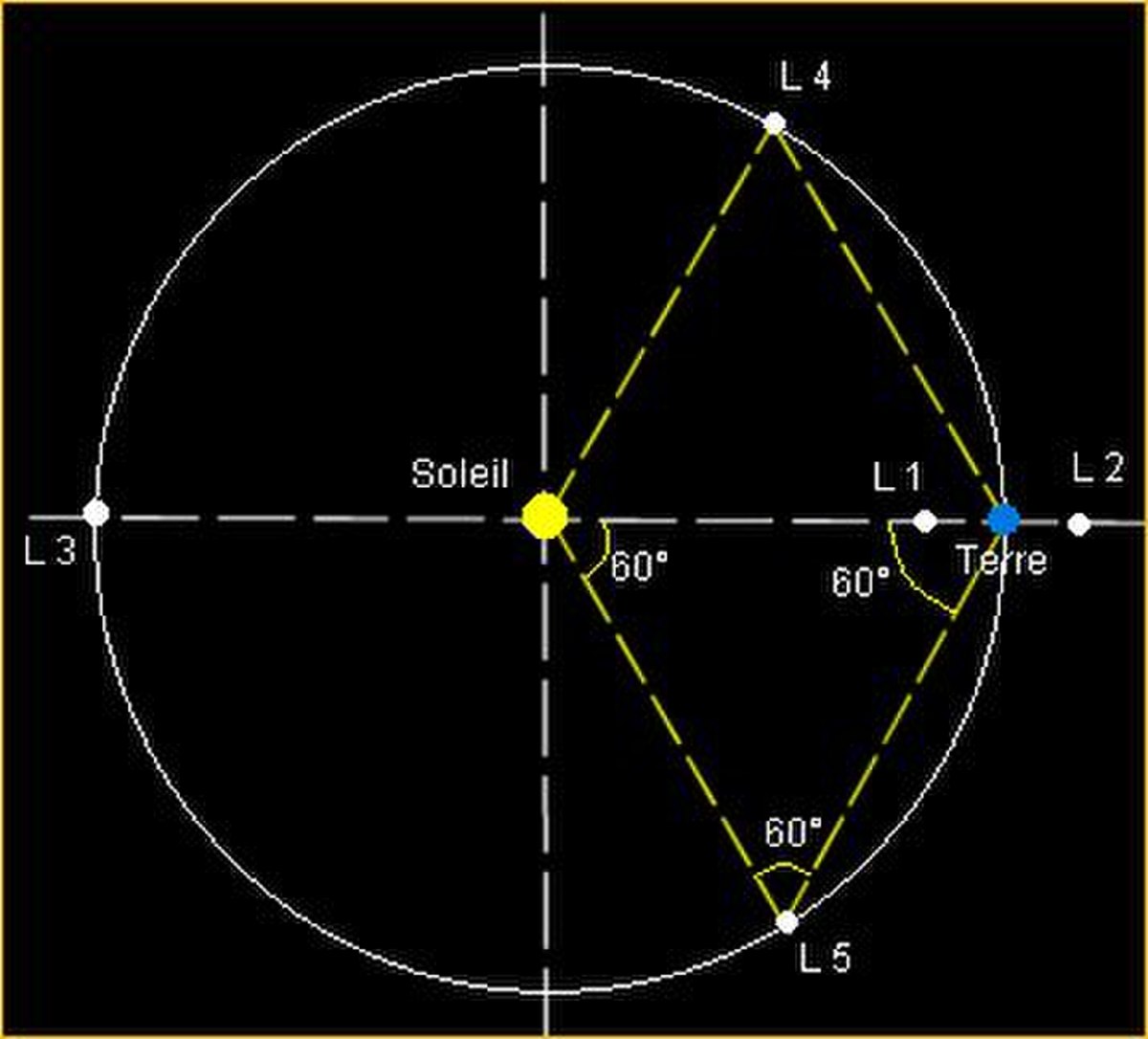
Trois des points de Lagrange sont situés sur l'axe reliant les deux corps. Dans le cas d'un grande dissymétrie de masse entre ceux-ci, deux points sont situés proches et de part et d'autre du corps peu massif, alors que le troisième est quasiment situé à l'opposé du corps peu massif par rapport au corps massif.

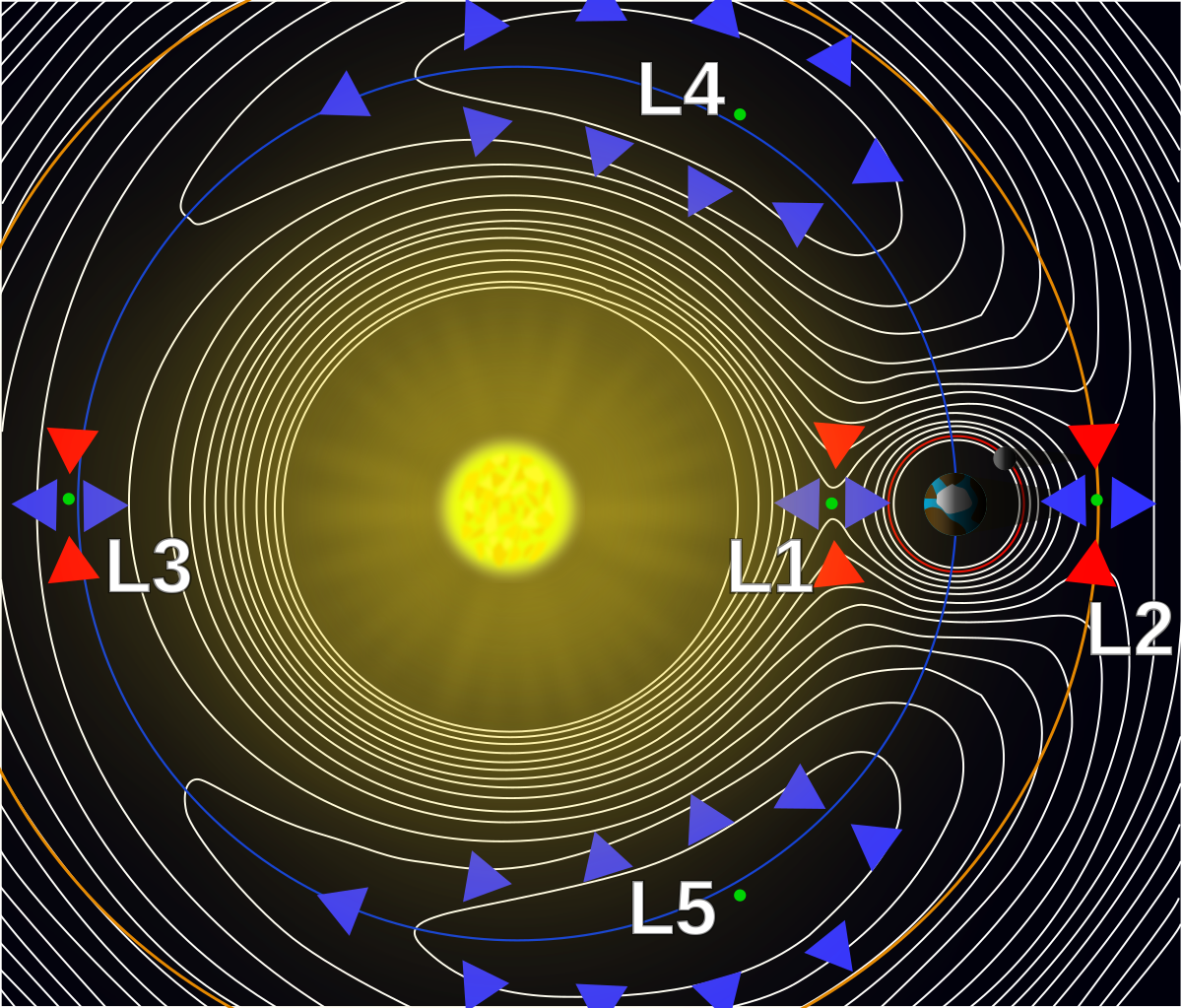
Si on donne en exemple les points de Lagrange du système Soleil-Terre, ces cinq points sont notés et définis comme suit (échelle non respectée) :

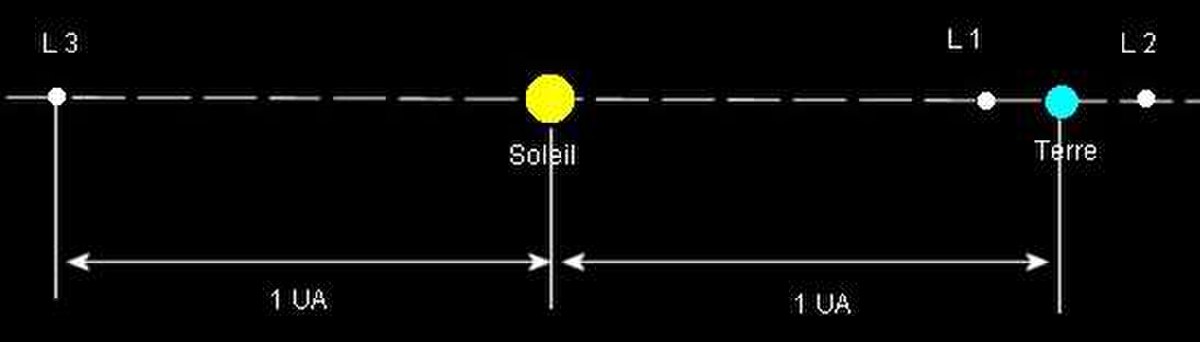
  • L : sur la ligne définie par les deux masses, entre celles-ci, la position exacte dépendant du rapport de masse entre les deux corps ; dans le cas où l'un des deux corps a une masse beaucoup plus faible que l'autre, le point L est situé nettement plus près du corps peu massif que du corps massif.
  • L : sur la ligne définie par les deux masses, au-delà de la plus petite. Dans le cas où l'un des deux corps a une masse beaucoup plus faible, la distance de L à ce corps est comparable à celle entre L et ce corps.
  • L : sur la ligne définie par les deux masses, au-delà de la plus grande. Dans le cas où l'un des deux corps est notablement moins massif que l'autre, la distance entre L et le corps massif est comparable avec celle entre les deux corps.
Les deux derniers points de Lagrange forment avec les deux corps des triangles équilatéraux.
  • L et L : sur les sommets des deux triangles équilatéraux dont la base est formée par les deux masses. Sans qu'il y ait de consensus précis, L est celui des deux points en avance sur l'orbite de plus petite des masses, dans son orbite autour de la grande, et L est en retard. Ces points sont parfois appelés points de Lagrange triangulaires ou points Troyens, du fait que c'est le lieu où se trouvent les astéroïdes troyens du système Soleil-Jupiter. Contrairement aux trois premiers points, ces deux derniers ne dépendent pas des masses relatives des deux autres corps.

Pertinence du concept

Le calcul ci-dessus fait référence à une configuration où les deux corps du système sont en orbite circulaire. Néanmoins, le concept de point de Lagrange prévaut pour tout type d'orbite, y compris elliptique. On peut donc définir ces points dans tout système à deux corps liés gravitationnellement. Par contre, les trajectoires, stables ou instables, autour des différents points de Lagrange dépendent explicitement de la circularité ou non de l'orbite des deux corps du système.

Stabilité

Lagrange points2.svg
Les points L4 et L5 bien que situés à des maxima du potentiel sont paradoxalement stables. L1, L2 et L3 qui sont des points-col sont instables.

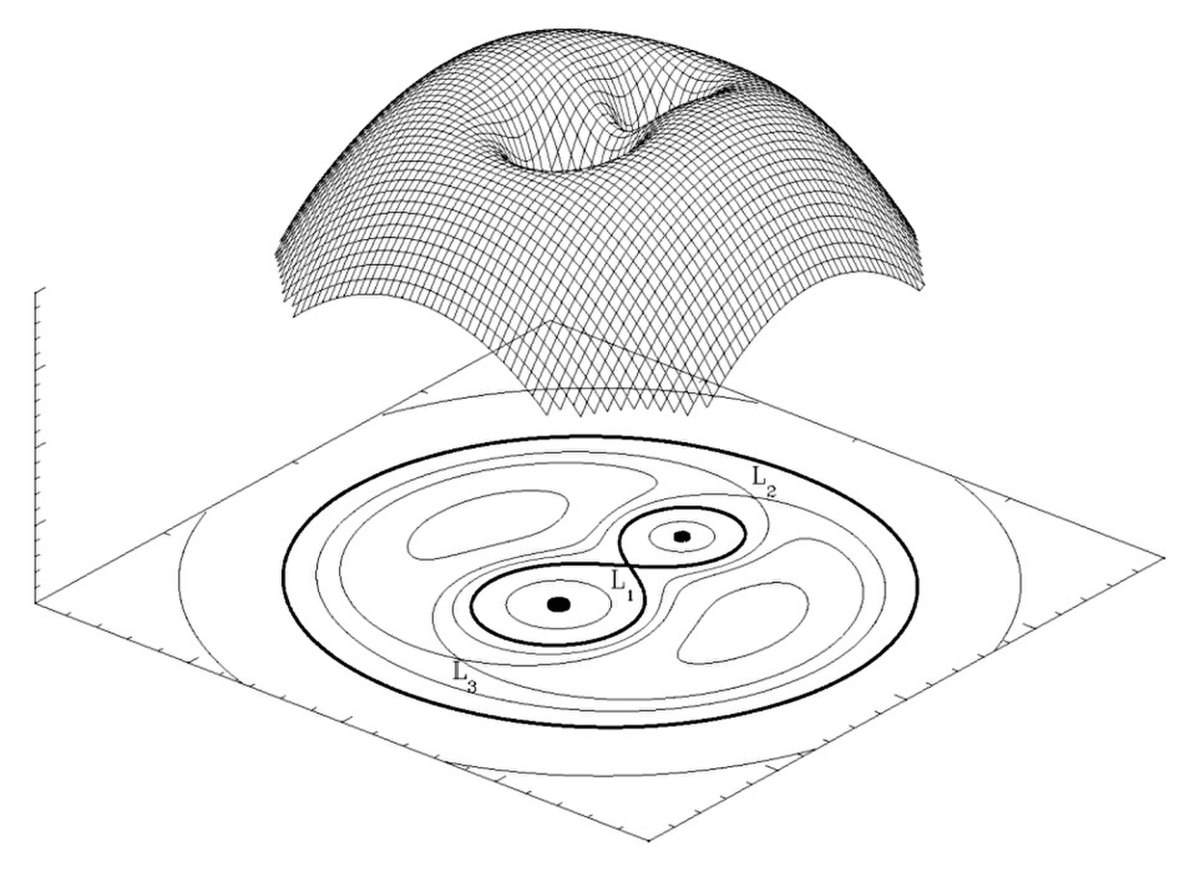
Le calcul ci-dessus n'indique en rien si les points de Lagrange sont stables. La stabilité ou non de ces points est du reste peu intuitive. Dans le référentiel tournant avec les deux corps, une particule d'épreuve peut être vue comme soumise à un potentiel incluant la contribution gravitationnelle et celle de la force centrifuge. Ce potentiel, noté Ω, s'écrit ainsi

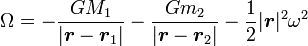
\Omega = - \frac{G M_1}{|\boldsymbol{r} - \boldsymbol{r}_1|} - \frac{G m_2}{|\boldsymbol{r} - \boldsymbol{r}_2|} - \frac{1}{2} |\boldsymbol{r}|^2 \omega^2 .

Tous les termes de ce potentiel sont négatifs et décroissent à mesure que l'on s'éloigne des masses (pour les deux premiers termes) ou du centre de gravité du système (pour le second). On peut ainsi montrer que les points de Lagrange L et L sont des maxima locaux du potentiel Ω (voir ci-dessous) et que les trois autres points sont des points selles. D'ordinaire, une position d'équilibre (déterminée par l'annulation des dérivées du potentiel) est stable uniquement si on se situe dans des minima locaux du potentiel. Cependant, étant donné que l'on est dans un référentiel tournant, le référentiel est non inertiel. Un objet se déplaçant dans ce référentiel, par exemple au voisinage d'une position d'équilibre, va être soumis à la force de Coriolis, et son mouvement ne dépend pas uniquement de la forme du potentiel. Pour étudier la stabilité des points de Lagrange, il faut donc tenir compte de la force de Coriolis.

Pour calculer la stabilité des points de Lagrange, il faut ainsi étudier l'équation du mouvement d'un objet situé au voisinage d'un de ces points. En notant δR le vecteur de coordonnées δX et δY donnant l'écart d'un tel objet à un des points de Lagrange (que l'on suppose confiné au plan orbital, l'équation du mouvement s'écrit

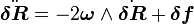
\ddot{\boldsymbol{\delta R}} = -2 \boldsymbol{\omega} \wedge \dot {\boldsymbol {\delta R}} + \boldsymbol {\delta f} ,

où δf représente la force par unité de masse exercée sur l'objet. Cette force est petite du fait qu'au point de Lagrange la force (constituée d'une composante gravitationnelle et de la force centrifuge) est nulle et que l'on se place à proximité d'un tel point. Cette force peut se calculer en termes d'un développement limité. Par exemple, pour la composante X, on a

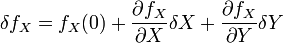
\delta f_X = f_X (0) + \frac{\partial f_X}{\partial X} \delta X + \frac{\partial f_X}{\partial Y} \delta Y .

Le premier terme correspond à la force s'exerçant au point de Lagrange, force qui est nulle par construction. Par ailleurs, la force dérivant d'un potentiel, on peut exprimer les dérivées de la force en termes de dérivées secondes du potentiel :

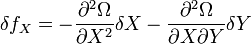
\delta f_X = - \frac{\partial^2 \Omega}{\partial X^2} \delta X - \frac{\partial^2 \Omega}{\partial X \partial Y} \delta Y .

On peut ainsi exprimer l'équation du mouvement en termes des composantes selon

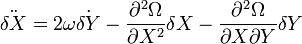
\ddot{\delta X} = 2 \omega \dot{\delta Y} - \frac{\partial^2 \Omega}{\partial X^2} \delta X - \frac{\partial^2 \Omega}{\partial X \partial Y} \delta Y ,
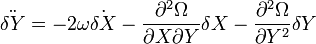
\ddot{\delta Y} = - 2 \omega \dot{\delta X}- \frac{\partial^2 \Omega}{\partial X \partial Y} \delta X - \frac{\partial^2 \Omega}{\partial Y^2} \delta Y .

Ce groupe d'équation peut être mis sous la forme d'un système de quatre équations différentielles du premier ordre :

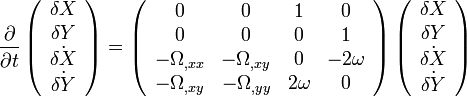
\frac{\partial}{\partial t}\left(\begin{array}{c} \delta X \\ \delta Y \\ \dot{\delta X} \\ \dot{\delta Y} \end{array} \right) = \left(\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -\Omega_{,xx} & - \Omega_{,xy} & 0 & -2 \omega \\ - \Omega_{,xy} & -\Omega_{,yy} & 2 \omega & 0 \end{array}\right) \left(\begin{array}{c} \delta X \\ \delta Y \\ \dot{\delta X} \\ \dot{\delta Y} \end{array} \right) ,

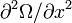
où les dérivées partielles du potentiel Ω ont été notée en indice précédé d'un virgule (par exemple, Ω correspond à \partial^2 \Omega / \partial x^2 ).

La stabilité du point de Lagrange considéré est obtenue en recherchant les solutions de cette équation. Pour cela, il suffit de trouver des solutions de type exponentielle, en eΓt. On va ainsi procéder à la diagonalisation de la matrice ci-dessus, que l'on notera A. Les valeurs propres trouvées vont correspondre aux quantités Γ ci-dessus, les écarts à la position d'équilibre étant alors une certaine combinaison d'au plus quatre exponentielles. La stabilité du système est assuré par le fait que les exponentielles ne croissent pas au cours du temps, c'est-à-dire que les quantités Γ sont soit négatives, soit complexes à partie réelle négatives. En fait, il n'est pas nécessaire de diagonaliser complètement la matrice, il suffit d'en trouver les valeurs propres, c'est-à-dire les solutions de l'équation

det(A − λI) = 0.

Ce déterminant s'écrit

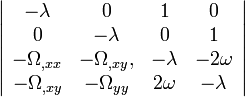
\left|\begin{array}{cccc} - \lambda & 0 & 1 & 0 \\ 0 & -\lambda & 0 & 1 \\ -\Omega_{,xx} & - \Omega_{,xy}, & - \lambda & - 2 \omega \\ - \Omega_{,xy} & - \Omega_{yy} & 2 \omega & -\lambda \end{array} \right| ,

et il vaut

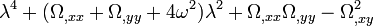
\lambda^4 + (\Omega_{,xx} + \Omega_{,yy} + 4 \omega^2) \lambda^2 + \Omega_{,xx} \Omega_{,yy} - \Omega_{,xy}^2 .

Cette équation peut se ramener à une équation polynomiale du second ordre en λ2. Les solutions de l'équation de départ sont donc deux couples de nombres opposés deux à deux. Pour que deux nombres opposés soient négatifs ou nuls ou alors de partie réelle négative ou nulle, il faut obligatoirement qu'ils soient des nombres imaginaires purs, donc que les solutions de l'équation en λ2 soient réelles et négatives. Pour que ces solutions soient réelles, il faut donc que le discriminant soit positif, soit ici

(\Omega_{,xx} + \Omega_{,yy} + 4 \omega^2)^2 - 4 (\Omega_{,xx} \Omega_{,yy} - \Omega_{,xy}^2) > 0.

Une fois ceci obtenu, il faut que les deux solutions réelles soient négatives, ce qui implique que simultanément leur somme soit négative et leur produit positif, ce qui implique

Ω,xx + Ω,yy + 4ω2 > 0,
\Omega_{,xx} \Omega_{,yy} - \Omega_{,xy}^2 > 0.

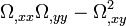
La stabilité d'un point de Lagrange est soumise à la réalisation de ces trois contraintes. Parmi ces contraintes, la dernière a une interprétation simple : le signe de la quantité \Omega_{,xx} \Omega_{,yy} - \Omega_{,xy}^2 détermine si la position considérée est un extrémum local ou un point selle. En l'occurrence, la positivité de cette quantité implique qu'elle doive être un extrémum local, condition nécessaire mais non suffisante à la stabilité du point de Lagrange. Quand cette quantité est négative, on a un point selle et le point de Lagrange est instable. Par contre, de façon plus surprenante, un point de Lagrange peut être stable s'il correspond à un maximum local du potentiel, c'est-à-dire que Ω +  Ω peut être négatif, pourvu que cette quantité ne dépasse pas la valeur critique de -4 ω2. En pratique, c'est ce qui se produit dans certains cas pour les points de Lagrange L et L. L'interprétation physique de cette situation est que la stabilité est alors assurée par la force de Coriolis. Un objet légèrement décalé d'un tel point va s'en éloigner dans un premier temps en façon radiale, avant de voir sa trajectoire incurvée par la force de Coriolis. Si le potentiel est partout décroissant autour du point, alors il est possible que la force de Coriolis force l'objet à tourner autour du point de Lagrange, à l'instar des nuages dans une dépression qui ne se dirigent pas vers le cœur de la dépression, mais sont contraints à une trajectoire circulaire autour de celui-ci.

Préliminaire

Pour étudier la stabilité des points de Lagrange, on va être amené à calculer les dérivées successives du potentiel. Ce potentiel fait intervenir la distance |r - r|. Il faut donc connaître les dérivées des différentes puissance d'une telle quantité. En coordonnées cartésiennes, cette quantité s'écrit

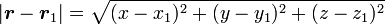
|{\boldsymbol{r}} - {\boldsymbol{r}}_1| = \sqrt{(x-x_1)^2 + (y - y_1)^2 + (z - z_1)^2} .

Sa dérivée par rapport à l'une des coordonnées x, y, z, collectivement notées x s'écrit donc

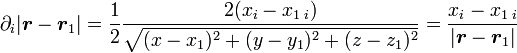
\partial_i |{\boldsymbol{r}} - {\boldsymbol{r}}_1| = \frac{1}{2} \frac{2 (x_i - x_{1\;i})}{\sqrt{(x-x_1)^2 + (y - y_1)^2 + (z - z_1)^2}} = \frac{x_i - x_{1\;i}}{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|} .

La dérivée d'une puissance p quelconque de cette grandeur est donc

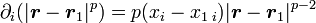
\partial_i (|{\boldsymbol{r}} - {\boldsymbol{r}}_1|^p) = p (x_i - x_{1\;i}) |{\boldsymbol{r}} - {\boldsymbol{r}}_1|^{p - 2} .

En adaptant ce résultat aux dérivées secondes des quantités intervenant dans le potentiel, on a

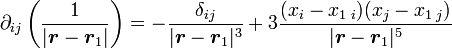
\partial_{ij} \left(\frac{1}{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|}\right) = - \frac{\delta_{ij}}{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|^3} + 3 \frac{(x_i - x_{1\;i}) (x_j - x_{1\;j})}{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|^5} ,

ce qui pour le potentiel complet donne

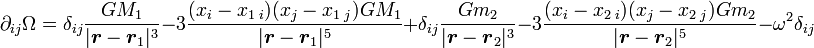
\partial_{ij} \Omega = \delta_{ij}\frac{G M_1}{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|^3} - 3 \frac{(x_i - x_{1\;i}) (x_j - x_{1\;j}) G M_1}{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|^5} + \delta_{ij}\frac{G m_2}{|{\boldsymbol{r}} - {\boldsymbol{r}}_2|^3} - 3 \frac{(x_i - x_{2\;i}) (x_j - x_{2\;j}) G m_2}{|{\boldsymbol{r}} - {\boldsymbol{r}}_2|^5} - \omega^2 \delta_{ij} ,

où δ représente le symbole de Kronecker. C'est la valeur de ces dérivées partielles qu'il faut calculer pour déterminer la stabilité des différents points de Lagrange. C'est pour les points de Lagrange L et L que ce calcul est le plus simple.

Cas des points de Lagrange L et L

Ces points se caractérisent par le fait que leur distance aux deux corps est identique et égale à R :

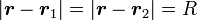
|{\boldsymbol{r}} - {\boldsymbol{r}}_1| = |{\boldsymbol{r}} - {\boldsymbol{r}}_2| = R .

Par ailleurs, on peut utiliser la troisième loi de Kepler pour passer des quantités du type G M / R3 à ω, et on connaît les coordonnées exactes des points de Lagrange. En évaluant les dérivées du potentiels au points de Lagrange L ou L, on a

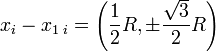
x_i - x_{1\;i} = \left(\frac{1}{2} R, \pm \frac{\sqrt{3}}{2} R \right) ,

et

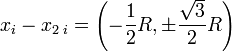
x_i - x_{2\;i} = \left(- \frac{1}{2} R, \pm \frac{\sqrt{3}}{2} R \right) ,

le signe + s'appliquant pour L et le signe - pour L. Au final, la matrice recherchée a pour composantes

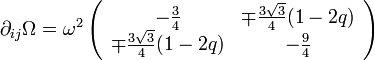
\partial_{ij} \Omega = \omega^2 \left(\begin{array}{cc} -\frac{3}{4} & \mp \frac{3\sqrt{3}}{4}(1-2q) \\ \mp \frac{3\sqrt{3}}{4}(1-2q) & -\frac{9}{4}\end{array} \right) .

Le déterminant de cette matrice vaut

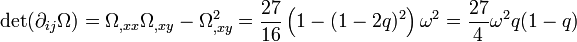
\det(\partial_{ij} \Omega) = \Omega_{,xx} \Omega_{,xy} - \Omega_{,xy}^2 = \frac{27}{16} \left(1 - (1 - 2 q)^2 \right) \omega^2 = \frac{27}{4} \omega^2 q (1 - q) ,

qui est toujours positif puisque q est confiné entre 0 et 1. Cette première condition de stabilité est établie. La seconde condition de stabilité s'écrit

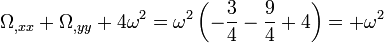
\Omega_{,xx} + \Omega_{,yy} + 4 \omega^2 = \omega^2\left(-\frac{3}{4} - \frac{9}{4} + 4 \right) = + \omega^2 ,

quantité là encore positive. Enfin, le discriminant donne

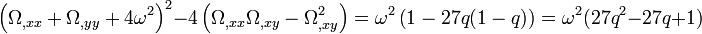
\left(\Omega_{,xx} + \Omega_{,yy} + 4 \omega^2\right)^2 - 4 \left(\Omega_{,xx} \Omega_{,xy} - \Omega_{,xy}^2\right) = \omega^2 \left(1 - 27 q (1 - q) \right) = \omega^2(27 q^2 - 27 q + 1) .

La stabilité des deux points est, au final, déterminée par la positivité de la quantité 27q2 − 27q + 1. Les zéros q, q de ce polynôme sont donnés par la formule usuelle, qui ici indique

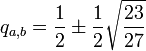
q_{a,b} = \frac{1}{2} \pm \frac{1}{2} \sqrt{\frac{23}{27}} .

Ce polynôme a ainsi des valeurs négatives sur la plage q \in \left]\frac{1}{2} - \frac{1}{2} \sqrt{\frac{23}{27}}, \frac{1}{2} + \frac{1}{2} \sqrt{\frac{23}{27}} \right[ \simeq ]0,\!03852, 0,\!96148[ . Ainsi, la stabilité de ces deux points de Lagrange n'est assurée que si la plus petite masse n'excède pas 3,852% de la masse totale, ou, de façon équivalente, que le rapport des deux masses n'excède pas 4,006%.

Cette condition est vérifiée pour toutes les configurations de type Soleil-Planète (où q n'excède pas environ un millième pour Jupiter), ou pour le système Terre-Lune (où q est de l'ordre de 1/80, soit 1,25%).

Cas des points de Lagrange L à L

Les trois points de Lagrange L à L sont situés sur l'axe reliant les deux corps. Dans la formule donne les dérivées secondes, les quantités y - y sont nulles, alors que leurs analogues en x s'identifient aux distances entre un des corps et le point de Lagrange considéré. En conséquence, la matrice des dérivées secondes s'écrit

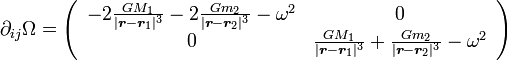
\partial_{ij} \Omega = \left(\begin{array}{cc} - 2\frac{G M_1}{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|^3} - 2\frac{G m_2}{|{\boldsymbol{r}} - {\boldsymbol{r}}_2|^3} - \omega^2 & 0 \\ 0 & \frac{G M_1}{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|^3} + \frac{G m_2}{|{\boldsymbol{r}} - {\boldsymbol{r}}_2|^3} - \omega^2 \end{array} \right) .

Le terme Ω est manifestement négatif. Le signe du déterminant de la matrice est déterminé par celui de Ω : si ce dernier est positif, alors le point de Lagrange est un point selle et il est instable. On peut réécrire ce terme en utilisant la troisième loi de Kepler :

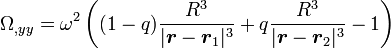
\Omega_{,yy} = \omega^2 \left((1 - q)\frac{R^3}{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|^3} + q \frac{R^3}{|{\boldsymbol{r}} - {\boldsymbol{r}}_2|^3} - 1 \right) .
Le cas de L

Le point de Lagrange L est situé entre les deux corps. Sa distance à ceux-ci, |r - r| et |r - r| est donc, à chaque fois, strictement inférieure à R. On a ainsi

\left.\Omega_{,yy}\right|_{L_2} = \omega^2 \left((1 - q)\frac{R^3}{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|^3} + q \frac{R^3}{|{\boldsymbol{r}} - {\boldsymbol{r}}_2|^3} - 1 \right) > \omega^2 \left( (1 - q) + q - 1 \right) = 0.

Cette quantité est donc strictement positive, ce qui assure que le déterminant est négatif, c'est-à-dire que L est un point selle, ce qui en fait un point instable.

Le cas de L et L

On pose, pour simplifier les notations,

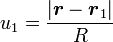
u_1 = \frac{|{\boldsymbol{r}} - {\boldsymbol{r}}_1|}{R} ,
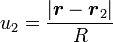
u_2 = \frac{|{\boldsymbol{r}} - {\boldsymbol{r}}_2|}{R} .

On s'intéresse donc au signe de la quantité

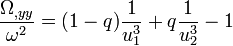
\frac{\Omega_{,yy}}{\omega^2} = (1 - q) \frac{1}{u_1^3} + q \frac{1}{u_2^3} - 1 ,

soit

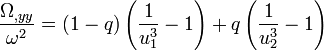
\frac{\Omega_{,yy}}{\omega^2} = (1 - q) \left(\frac{1}{u_1^3} - 1\right) + q \left(\frac{1}{u_2^3} - 1\right) ,

sachant que u et u sont reliés entre eux par le fait que leur différence est égale à 1 et qu'ils définissent un point de Lagrange, soit la relation

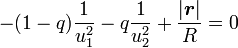
- (1 - q) \frac{1}{u_1^2} - q \frac{1}{u_2^2} + \frac{|{\boldsymbol{r}}|}{R} = 0 .

La distance du point de Lagrange au centre de gravité du système peut s'écrire, pour le point L,

,

relations que l'on peut combiner en

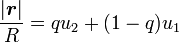
\frac{|{\boldsymbol{r}}|}{R} = q u_2 + (1 - q) u_1 .

La position du point L est donc donnée par

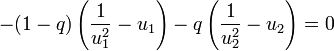
- (1 - q) \left(\frac{1}{u_1^2} - u_1\right) - q \left(\frac{1}{u_2^2} - u_2 \right) = 0 .

On pose alors

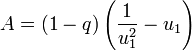
A = (1 - q) \left(\frac{1}{u_1^2} - u_1\right) ,
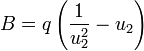
B = q \left(\frac{1}{u_2^2} - u_2 \right) .

On a donc, d'une part

A + B = 0,

et, d'autre part

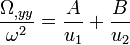
\frac{\Omega_{,yy}}{\omega^2} = \frac{A}{u_1} + \frac{B}{u_2} .

Autrement dit,

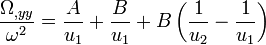
\frac{\Omega_{,yy}}{\omega^2} = \frac{A}{u_1} + \frac{B}{u_1} + B \left(\frac{1}{u_2} - \frac{1}{u_1} \right) .

Le premier terme du membre de droite est nul en vertu de la relation A + B = 0. Il reste donc

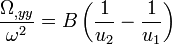
\frac{\Omega_{,yy}}{\omega^2} = B \left(\frac{1}{u_2} - \frac{1}{u_1} \right) .

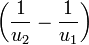
Or, pour le point L, on est situé plus près du corps 2 que du corps 1. Par conséquent, u est plus petit que u, et, par conséquent, \left(\frac{1}{u_2} - \frac{1}{u_1} \right) est positif. Le signe de la dérivée seconde correspond donc à celui de B, qui lui-même est déterminé par la valeur de u : si cette quantité est supérieure à 1, alors B est négatif, alors que, dans le cas contraire, B est positif, ce qui implique que le point est instable. Le point de Lagrange L est situé au-delà du corps 2. La force totale (gravitationnelle plus centrifuge) s'exerçant dans cette région est d'abord tournée vers le corps 2 quand on est proche de celui-ci, puis s'annule en L et est après dirigée à l'opposé de L. Au point tel que u vaut 1, la composante de cette force, selon l'axe reliant les deux corps, est donnée (à une constante multiplicative positive près) par

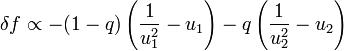
\delta f \propto - (1 - q) \left(\frac{1}{u_1^2} - u_1\right) - q \left(\frac{1}{u_2^2} - u_2 \right) ,

avec, ici,

u2 = 1,
u1 = 2,

soit

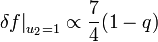
\left.\delta f \right|_{u_2 = 1} \propto \frac{7}{4} (1 - q) .
Cette quantité étant strictement positive, le point u = 1 de l'axe est situé au-delà du point L. En conséquence, au point L, u est inférieur à 1, donc B est positif, donc le point est bien un point selle, ce qui assure de son instabilité. Une démonstration strictement analogue peut être faite pour le point L, ce qui achève la démonstration de leur instabilité du fait de leur caractère de point selle.
 

Temps caractéristiques en L et L pour les systèmes à grande hétérogénéité de masse

Une des applications les plus importantes de l'instabilité des points de Lagrange, L et L, réside dans le fait que des satellites artificiels peuvent être envoyés en ces points du système Terre-Soleil (voir ci-dessous). Pour de tels satellites, des corrections de trajectoires régulières doivent être appliquées afin de conserver le satellite au voisinage du point. Ce temps caractéristique peut être évalué dans le cas où le rapport de masse des deux corps du système est élevé. Dans ce cas, le temps caractéristique γ-1 d'instabilité est donné par

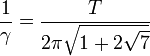
\frac{1}{\gamma} = \frac{T}{2 \pi \sqrt{1 + 2\sqrt{7}}} ,

où T est la période orbitale du système. Dans le cas du système Terre-Soleil, où T est légèrement supérieur à 365 jours, le temps caractéristique d'instabilité est alors de 23 jours et 4 heures.

Par ailleurs, la composante stable de la trajectoire se fait à la pulsation

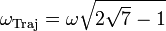
\omega_{\rm Traj} = \omega \sqrt{2 \sqrt{7} - 1} ,

soit, de façon équivalente, avec la période

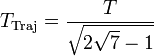
T_{\rm Traj} = \frac{T}{\sqrt{2 \sqrt{7} - 1}} ,

ce qui, dans le même cas de figure que ci-dessus, donne une période de 176 jours.

L'équation donnant les valeurs propres du système est toujours

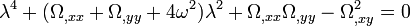
\lambda^4 + (\Omega_{,xx} + \Omega_{,yy} + 4 \omega^2) \lambda^2 + \Omega_{,xx} \Omega_{,yy} - \Omega_{,xy}^2 = 0 ,

avec, pour les points L et L,

Ω,xy = 0,
Ω,xx = − 2Ω,yy − 3ω2,
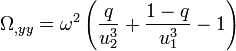
\Omega_{,yy} = \omega^2 \left(\frac{q}{u_2^3} + \frac{1 - q}{u_1^3} - 1\right) .

en se restreignant aux termes d'ordre le plus bas en q, u vaut 1, et u est déterminé par la relation donnée par le premier tableau de cette page. On a ainsi

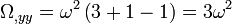
\Omega_{,yy} = \omega^2 \left(3 + 1 - 1\right) = 3 \omega^2 ,
Ω,xx = − 9ω2.

L'équation polynomiale devient alors

λ4 − 2ω2λ2 − 27ω4 = 0,

dont les solutions sont

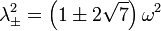
\lambda_\pm^2 = \left(1 \pm 2 \sqrt{7}\right) \omega^2 .

La solution positive à cette équation indique que les écarts au point d'équilibre croissent exponentiellement au cours du temps selon la relation

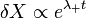
\delta X \propto e^{\lambda_+ t} ,

avec

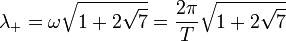
\lambda_+ = \omega \sqrt{1 + 2 \sqrt{7}} = \frac{2 \pi}{T} \sqrt{1 + 2 \sqrt{7}} .

Le temps caractéristique associé est donc

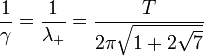
\frac{1}{\gamma} = \frac{1}{\lambda_+} = \frac{T }{2 \pi \sqrt{1 + 2 \sqrt{7}}} .

De la même façon, il existe des trajectoires périodiques dont la pulsation est donnée par les racines complexes de l'équation, soit

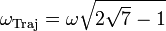
\omega_{\rm Traj} = \omega \sqrt{2 \sqrt{7} - 1} ,

c'est-à-dire une période de

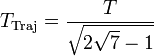
T_{\rm Traj} = \frac{T}{\sqrt{2 \sqrt{7} - 1}} .
 

La structure des orbites en présence d'instabilité

Une fois les valeurs propres d'un point instable connues, une trajectoire au voisinage d'un point de Lagrange va être une combinaison linéaire des vecteurs propres associés aux valeurs propres. En notant λ' l'une de ces valeurs propres, le vecteur propre associé a pour composantes

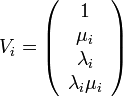
V_i = \left(\begin{array}{c} 1 \\ \mu_i \\ \lambda_i \\ \lambda_i \mu_i \end{array}\right) ,

avec

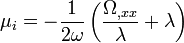
\mu_i = - \frac{1}{2 \omega} \left(\frac{\Omega_{,xx}}{\lambda} + \lambda \right) ,

et une trajectoire est de la forme

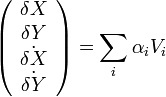
\left(\begin{array}{c} \delta X \\ \delta Y \\ \dot{\delta X} \\ \dot{\delta Y} \end{array}\right) = \sum_i \alpha_i V_i ,

où les quantités α sont des nombres quelconques déterminés par la valeur des δX, δY et de leur dérivée à un instant donné. Dans le cas des trois points de Lagrange instables, le déterminant de la matrice des dérivées secondes est négatif, ce qui implique que le discriminant de l'équation du second degré en λ2 possède des racines réelles de signe opposé, et, qu'au final, les valeurs propres recherchées sont deux nombres imaginaires purs opposés et deux nombres réels opposés. Une trajectoire générique comprend donc, dans le plan orbital, une composante périodique (liée aux racines imaginaires pures), une composante amortie (liée à la racine réelle positive), et une composante instable. Pour une position δX, δY donnée, il est toujours possible de choisir une vitesse telle que les deux vecteurs propres aux racines réelles ne contribuent pas à la solution correspondante. La trajectoire obtenue est alors périodique, la période étant donnée par la racine complexe. Une telle solution n'est cependant pas stable. Un écart de trajectoire infime va en réalité rajouter à la trajectoire une composante instable, qui va, peu à peu, éloigner la trajectoire de sa composante périodique. On dit que la trajectoire obtenue n'est pas dynamiquement stable. Ceci est une généralisation du fait qu'un objet situé exactement sur un point de Lagrange instable est dans une situation instable : un petit écart à cette position d'équilibre, inéluctablement généré par les perturbations causées par les autres corps du système, finira par éloigner l'objet de sa position initiale. La même chose se produit pour des trajectoires situées autour du point d'équilibre instable.

Calcul de la position des points de Lagrange
Applications
- Introduction - Historique - Calcul de la position des points de Lagrange - Définition - Pertinence du concept - Stabilité - Applications
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
miniature
Comment des impacts géants vaporisent les corps planétaires ☄️
miniature
Les Américains riches vivent moins longtemps que les Européens pauvres 💰
miniature
Attention à ce riz naturellement riche en arsenic 🍚
miniature
L'intelligence artificielle contre la mort subite 💀
miniature
L'inévitable formation d'un océan de magma basal sur Terre 🔥
miniature
Découverte d'une plante étrange sans chlorophylle 🌱
miniature
Existe-t-il des mélodies naturelles ? 🎶
miniature
Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽
miniature
L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡
miniature
1
Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺
miniature
Imprimer en 3D avec la lumière du soleil ☀️
miniature
La pollution atmosphérique nuit gravement au cerveau 🧠
miniature
Le trou noir supermassif Ansky vient de se réveiller ⚫
miniature
1
Voici ce qui rend notre cerveau vraiment unique 🧠
miniature
Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩
miniature
Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬
miniature
La physique révèle les secrets d'un strike parfait au bowling 🎳
miniature
Le TDAH associé à la démence 🧠
Page générée en 0.180 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise