Plus grand commun diviseur - Définition

Notations

Le PGCD de deux entiers a et b est souvent noté : PGCD(a,b) ou pgcd(a,b). De même, le pgcd d'une séquence d'entiers a_i sera notée pgcd(a_i) ou PGCD(a_i).

Certains auteurs notent le pgcd de deux entiers a et b sous la forme . Cette notation fait référence aux ensembles ordonnés : tout diviseur commun à a et b divise leur pgcd (voir ci-dessous).

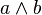
Les anglophones le nomment greatest common divisor, noté : gcd(a,b).

Exemple

On cherche le PGCD de 15 et 12.

Les diviseurs positifs de 15 sont : 1, 3, 5, 15.

Les diviseurs positifs de 12 sont : 1, 2, 3, 4, 6, 12.

On obtient donc d_12,15 = {1,3}

On en déduit pgcd(12, 15) = 3.

Pour trouver le PGCD de deux nombres plus grands, on peut utiliser l'algorithme d'Euclide

Cas du zéro

Certaines définitions du PGCD autorisent le calcul du PGCD d'un entier quelconque avec 0. Pour tout n entier, pgcd(0,n) = n.

Cette propriété reste vraie pour n=0.

Donc pgcd(0,0)=0 (c'est la réponse donnée par les calculatrices : elle ne peut se justifier par la définition du PGCD du premier paragraphe).

Ce n'est pas une simple convention, mais la conséquence de la définition formelle du PGCD.

En effet, ce résultat devient évident quand on adopte la (a) + (b) = (pgcd(a,b)) ("(a)" signifiant "idéal engendré par l'élément a") comme définition du PGCD, ce qui se fait sans problème si on travaille sur les nombres entiers, puisque leur ensemble est un anneau principal.

Il s'agit d'ailleurs du seul cas pour lequel il n'y a pas à choisir entre un PGCD positif et un négatif.

Propriétés

Soit

• 
• 
• 
• 
• 
• 
• 
• 
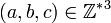
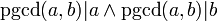
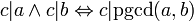
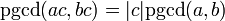
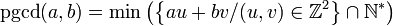
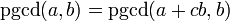
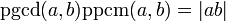
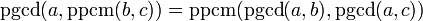
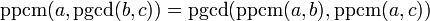
• , on peut étendre à un nombre arbitraire d'éléments
• Géométriquement, pgcd(a,b) est le nombre de points de coordonnées entières sur le segment d'extrémités des points (0,0) et (a,b), sans compter (0,0).

Calcul

On peut calculer le PGCD de deux nombres en écrivant leur décomposition en produit de facteurs premiers et en considérant le produit de certains facteurs premiers communs. Dans la pratique, on utilise rarement cette méthode du fait de sa lenteur, excepté dans les cas évidents (par exemple pour 4 et 6, on trouve immédiatement 4=2*2 et 6=2*3, d'où PGCD(4,6)=2).

Une méthode beaucoup plus efficace est l'algorithme d'Euclide.

Généralisations

PGCD de fractions

Dans ce paragraphe, on utilise la définition suivante: d est un pgcd de a et b si d divise a et b et d est divisible par tout élément divisant a et b. (paragraphe 2)

Premier point de vue: c'est le plus évident: on se place dans le corps des rationnels. Alors pour p1/q1 et q2/p2 deux rationnels non tous deux nuls, tout rationnel non nul est un PGCD de p1/q1 et q2/p2 (Q étant un corps, tout rationnel autre que 0 divise 1, et 1 divise tout rationnel). Par convention, on choisit 1 comme PGCD. Dans le cas où les deux fractions sont nulles, le PGCD vaut encore 0.

Note: on montre que A est un corps si et seulement si A est un anneau unitaire dont les seuls idéaux sont {0} et A. On comprend facilement, avec la définition du paragraphe 2.1, que deux éléments non tous deux nuls de A admettent n'importe quel élément non nul de A comme PGCD, et on choisit 1 (le neutre de la seconde loi) par convention. La notion de PGCD n'a donc pas beaucoup d'intérêt dans un corps!

Deuxième point de vue: il consiste à considèrer qu'une fraction p/q en divise une autre p'/q' non pas s'il existe une fraction a/b telle que p/q*a/b=p'/q' (toujours vrai si p ne vaut pas 0: prendre a=q*p' et b=p*q') mais seulement s'il existe un entier c tel que p/q*c=p'/q'.

De façon analogue au paragraphe sur les idéaux, un pgcd de p1/q1 et q2/p2 est une fraction p/q telle que . Mais attention, les objets manipulés ici ne sont pas des idéaux, ni des pseudo sous-anneaux de Q, seulement des sous-groupes.

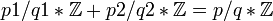
Finalement, on trouve p=+/- pgcd(p1,p2) et q=ppcm(q1,q2).

De même, on a ppcm(p1/q1,p2/q2)= +/- ppcm(p1,p2)/pgcd(q1,q2)

Le PGCD obtenu suivant le deuxième point de vue est également un PGCD possible quand on se place sur le corps Q. Les calculatrices et les logiciels de calcul choisissent l'un ou l'autre suivant le choix des programmeurs (par exemple Maple adopte le premier point de vue, la Casio Graph 100+ et la TI-92 le second).

Un inconvénient du second point de vue est que le PGCD d'une famille infinie de rationnels n'existe pas toujours. Par exemple la famille des fractions 1/n, n allant de 1 à l'infini parmi les entiers, n'admet pas de PGCD.

Cas des réels

On peut encore étendre les définitions précédentes avec des nombres réels: le premier point de vue conduit à un PGCD de 1 pour tout couple de réels non tous deux nuls.

Le second point de vue dit que pour deux réels quelconques a et b, s'il existe un réel c tel que a=u*c et b=v*c avec u et v rationnels, on choisit PGCD(a,b)=|c|*PGCD(u,v), suivant la définition des PGCD de rationnels vue ci-dessus (2e point de vue).

Pour deux réels a et b tels que a/b soit irrationnel (si b=0 on est dans la situation précédente) on est obligé de revenir au premier point de vue d'où PGCD(Pi, )=1; à noter que le PPCM le même problème, mais il est déterminé par PGCD(a,b)*PPCM(a,b)=|a*b|. (PPCM(Pi, )=Pi* )

Chaque calculateur se plaçant dans la continuité de son comportement concernant les rationnels, Maple répond suivant le premier point de vue, la Casio Graph 100+ selon le second ; la Ti-92 n'a pas de réponse.

Polynômes à coefficients réels

Le PGCD dans l'anneau vérifie la définition donnée plus haut. Mais cette fois il y a une infinité de PGCD possibles pour 2 polynômes : en effet tout PGCD des polynômes A et B multiplié par un réel non nul est aussi un PGCD de A et B. Pour définir un PGCD unique il y a deux conventions possibles: ou bien on pose par convention que le PGCD doit être un polynôme unitaire, ou bien on choisit le polynôme dont le coefficient dominant est le PGCD des coefficients dominants de A et B, en employant la définition du paragraphe précédent pour les PGCD de réels.

À titre d'exemple, le logiciel (propriétaire) de calcul formel Maple choisit la première option quand les polynômes sont à coefficients entiers, la seconde sinon, tandis que les calculatrices Casio optent toujours pour la seconde convention.

Si l'on ne dispose pas de moyen automatisé (logiciel ou calculatrice), on peut toujours trouver « manuellement » le PGCD de 2 polynômes en transposant pour ces polynômes l'algorithme d'Euclide servant à trouver le PGCD de deux nombres entiers (voir ici comment on peut effectuer la division de 2 polynômes).

Dans les anneaux commutatifs

Par extension, le plus grand commun diviseur peut être défini plus généralement pour les éléments d'un anneau commutatif arbitraire, pas forcément unitaire (certains diraient: pseudo-anneau). Le plus grand commun diviseur d'une famille a_i d'éléments de A non tous nuls est le plus grand diviseur commun aux a_i au sens de la division.

L'existence d'un tel élément (tout comme du PPCM) est certaine dans un anneau factoriel, pas toujours dans d'autres anneaux.

Par exemple, dans l'anneau , 4 et admettent 2 et comme diviseurs, mais aucun élément divisible simultanément par 2 et ne les divise.

Le PGCD de a et b n'est pas toujours unique, mais si A est intègre alors deux quelconques PGCD de a et b sont des éléments associés.

Dans le pseudo-anneau 2 * Z / 20Z, [8] et [12] admettent comme pgcd possibles [4], [8], [12], [16] ([2]*[4]=[8], [4]*[8]=[32]=[12], [8]*[12]=[96]=[16], [4]*[16]=[64]=[4]), qui ne sont pas associés.

Dans un anneau principal, il existe c et d éléments de A (non uniques) tels que ac + bd = pgcd(a,b) (théorème de Bachet-Bézout)

Si A est un anneau euclidien alors une forme de l'algorithme d'Euclide peut être utilisée pour calculer le PGCD.

L'unicité peut dans certains cas être rétablie en posant une contrainte supplémentaire. Par exemple dans l'anneau des polynômes à coefficients complexes, le PGCD est unique si on exige qu'il soit un polynôme unitaire.

D'ailleurs dans le cas des nombres entiers, l'unicité du PGCD est obtenue avec la convention "le PGCD est un nombre positif". Sans cette convention, la définition ci-dessus donne deux PGCD distincts, opposés.

Tout ce qui précède se généralise à un nombre arbitraire ou même infini d'éléments, sauf l'algorithme d'Euclide.

Définition par les idéaux

La définition de ce paragraphe est un peu plus générale que celle du paragraphe précédent, et permet de définir des PGCD dans des cas où ils ne pourraient l'être suivant la définition précédente.

Dans l'anneau commutatif A, on note (x) l'idéal principal engendré par l'élément x, ie l'intersection de tous les idéaux de A contenant x, (l'ensemble des éléments xy, y décrivant A si A est unitaire).

Pour a et b éléments de A, (a)+(b) est également un idéal.

Alors d est un pgcd de a et b ssi (d) est le plus petit idéal engendré par un seul élément et incluant (a)+(b), ie (a)+(b) ⊂(d) et pour tout x ⊂ A, (a)+(b) ⊂ (x) (ce qui équivaut à "x est un diviseur de a et b" si A est unitaire) ⇒ (d) ⊂ (x) (ce qui équivaut à "x est un diviseur de d" si A est unitaire).

Dans le pseudo-anneau (anneau non unitaire) 2Z, 8 et 12 ont pour PGCD possibles 4 et -4… En effet, (8)+(12) ⊂ (4) = (-4) = 4Z, et pourtant il n'existe pas dans 2Z d'élément x tel que 4*x=12.

Dans un anneau principal, ce qui précède équivaut à (a)+(b) = (d)

Comme plus haut, il n'y a pas unicité du pgcd.

Ici encore, on peut étendre à un nombre arbitraire voire infini d'éléments.

Anneaux non-commutatifs

Dans un anneau non-commutatif, un élément peut admettre des "diviseurs à droite" et des "diviseurs à gauche". On peut dans certain cas définir un PGCD à droite et/ou un PGCD à gauche. Mais l'existence de l'un n'implique pas forcément celle de l'autre, et l'existence commune n'implique pas forcément l'égalité.

Demander à un calculateur électronique le PGCD de deux matrices n'est pas forcément interprété au sens de l'algèbre linéaire. Par exemple une TI-92 interrogée sur le PGCD de deux matrices de même taille répond en donnant la matrice composée des PGCD des éléments de même position des deux matrices.