Plan d'expérience - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Position du problème - Limites des plans expérimentaux exhaustifs - En sciences appliquées (plans expérimentaux) - Les plans factoriels - Exemple

Les plans factoriels

Parmi les différents plans expérimentaux, les plans factoriels sont courants car ils sont les plus simples à mettre en œuvre et ils permettent de mettre en évidence très rapidement l'existence d'interactions entre les facteurs.

L'hypothèse de base est d'assigner à chaque facteur (normalisé) sa valeur la plus basse ( $- 1$ ) et sa valeur la plus haute ( $+ 1$ ). Ainsi, pour $k$ facteurs, on se retrouve avec un ensemble de $2 k$ valeurs possibles.

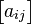
Sans entrer dans les détails, la matrice d'expérience $\begin{bmatrix} a_{ij}\end{bmatrix}$ possède alors des propriétés intéressantes (on a par exemple: $a T$ $\cdot$ $a$ = $k$ $\cdot$ $1$ ) qui sont largement exploitées par les logiciels qui établissent des plans expérimentaux. En particulier, l'ajout d'expériences supplémentaires ainsi que des algorithmes de randomisation efficace du plan d'expérience initial permettent de mettre en évidence des biais systématiques et de les supprimer ou alors de mettre en évidence l'influence d'une variable cachée dont il faut tenir compte.

Pour reprendre l'exemple ci-dessus, on se retrouve avec un plan à 12 expériences (2 températures extrêmes, 2 concentrations extrêmes et 3 paires d'électrodes).

Travaillons avec la température et la concentration normalisée:

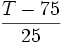
$t$ = $\frac {T-75} {25}$

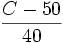
$c$ = $\frac {C-50} {40}$

On cherche maintenant uniquement des dépendances linéaires en $t$ et en $c$ , c'est-à-dire une relation du type:

$I X$ ( $t$ , $c$ ) = $b 1$ $t$ + $b 2$ $c$ + $b 3 t$ $c$ pour $X$ = $1$ , $2$ ou $3$ selon le type d'électrode.

En effectuant les mesures du courant aux 4 points (50 °C,10%) , (50 °C,90%) , (100 °C,10%), (100 °C,90%) correspondant aux points ( $- 1$ , $- 1$ ),( $- 1$ , $+ 1$ ), ( $+ 1$ , $- 1$ ) et ( $+ 1$ , $+ 1$ ) dans l'espace des facteurs réduits, on a, pour chaque type d'électrode, on est ramené à un plan factoriel $22$

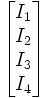
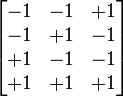
$\begin{bmatrix} I_1 \\ I_2 \\ I_3 \\ I_4\end{bmatrix}$ = $\begin{bmatrix} -1 & -1 & +1 \\ -1 & +1 & -1 \\ +1 & -1 & -1 \\ +1 & +1 & +1\end{bmatrix}$ $\cdot$ $\begin{bmatrix} b_1 \\ b_2 \\ b_3\end{bmatrix}$

On vérifie effectivement que $a T$ $\cdot$ $a$ = $k$ $\cdot$ $1$ , et on obtient la résolution du système:

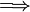
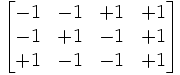
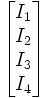
$\Longrightarrow$ $\begin{bmatrix} b_1 \\ b_2 \\ b_3\end{bmatrix}$ = $\frac {1} {4}$ $\begin{bmatrix} -1 & -1 & +1 & +1 \\ -1 & +1 & -1 & +1 \\ +1 & -1 & -1 & +1\end{bmatrix}$ $\cdot$ $\begin{bmatrix} I_1 \\ I_2 \\ I_3 \\ I_4 \end{bmatrix}$

Soit:

$b 1$ = $\frac {1} {4}$ (- $I 1$ - $I 2$ + $I 3$ + $I 4$ )

$b 2$ = $\frac {1} {4}$ (- $I 1$ + $I 2$ - $I 3$ + $I 4$ )

$b 3$ = $\frac {1} {4}$ ( $I 1$ - $I 2$ - $I 3$ + $I 4$ )

Ainsi, moyennant quelques précautions, on a ramené une étude d'un processus non analytique constitué de 162 expériences distinctes à un processus d'une douzaine d'expériences, qui donne des résultats intéressants sur les intervalles considérés, en particulier sur l'existence et l'amplitude des interactions entre les différents facteurs.

Exemple

Supposons que l'on souhaite caractériser un processus électrolytique par la mesure du courant entre les électrodes.

Pour une solution d'électrolyte donnée, un modèle grossier laisse supposer que ce courant va dépendre de trois facteurs principaux: (1) la dilution de la solution $C$ , comprise entre 10% et 90%, (2) la température de la solution $T$ , comprise entre 50 °C et 100 °C, et (3) la nature des électrodes utilisées (étain, or et en platine). Dans ces conditions, en prenant des pas de 10% pour la concentration et de 10 °C pour la température, le plan expérimental exhaustif sera constitué de 9x6x3, soit 162 expériences indépendantes qu'il faudra faire dans des conditions par ailleurs identiques.

En supposant que chaque expérience prend 1 heure (en comptant le temps de préparation), l'étude de ce simple processus ne demanderait pas moins de 5 semaines de travail à plein temps (35h par semaine). De plus, des expériences étalées sur un aussi grand laps de temps pourrait faire intervenir des facteurs non-connus mais variant sur la durée de cette étude et pouvant fausser les résultats.

On comprend aisément que les points relevés ci-dessus deviennent dramatiques dès que l'on a affaire à des processus un peu plus complexes et le coût expérimental d'une étude exhaustive devient vite prohibitif, voir inapplicable. C'est un problème courant dans les processus industriels qui exigent une reproductibilité et un contrôle qualité total.

La manière correcte d'aborder un plan d'expérience optimal est de procéder d'une manière tout à fait analogue au principe de la droite de régression en supposant que l'on a des dépendances linéaires (ou tout au plus quadratiques) du processus dans chacune de ces variables ainsi que des interactions entre les variables. On se basera le plus souvent sur des hypothèses simples et/ou des expériences limites pour se donner une idée de l'existence ou non de dépendances croisées.

Reprenons le processus décrit plus haut en supposant que en plus de $T$ et $C$ , on définisse $m$ comme une grandeur physique qui caractérise la matière de l'électrode (par exemple son poids moléculaire ou son électrovalence, etc.):

On souhaite le décrire par une formule simplifiée du type:

F(T,C,m)=

$b 1$ $\cdot$ $T 2$ + $b 2$ $\cdot$ $C 2$ + $b 3$ $\cdot$ $m 2$ + $b 4$ $\cdot$ $T$ + $b 5$ $\cdot$ $C$ + $b 6$ $\cdot$ $m$ + $b 7$ $\cdot$ $T$ $\cdot$ $C$ + $b 8$ $\cdot$ $T$ $\cdot$ $m$ + $b 9$ $\cdot$ $C$ $\cdot$ $m$ + $b 10$ $\cdot$ $T$ $\cdot$ $C$ $\cdot$ $m$ + $b 11$ $\cdot$ $T 2$ $\cdot$ $C$ + $b 12$ $\cdot$ $T 2$ $\cdot$ $m$ + $b 13$ $\cdot$ $C 2$ $\cdot$ $T$ + $b 14$ $\cdot$ $C 2$ $\cdot$ $m$ + $b 15$ $\cdot$ $T$ $\cdot$ $m 2$ + $b 16$ $\cdot$ $C$ $\cdot$ $m 2$

Pour simplifier, on supposera raisonnablement que les termes en $T 2$ $\cdot$ $C$ , $T 2$ $\cdot$ $m$ , $C 2$ $\cdot$ $T$ , $C 2$ $\cdot$ $m$ , $T$ $\cdot$ $m 2$ et $C$ $\cdot$ $m 2$ sont négligeables par rapport aux termes du premier ordre, ce qui revient à dire que les coefficients $b 11$ , $b 12$ , $b 13$ , $b 14$ , $b 15$ et $b 16$ sont nuls (en général, le terme en $T$ $\cdot$ $C$ $\cdot$ $m$ est aussi négligeable).

Il reste alors 10 variables $b 1$ , .. , $b 10$ à déterminer pour avoir une connaissance analytique du processus dans les intervalles spécifiés.

On « choisit » 10 points dans l'espace ( $T$ , $C$ , $m$ ), pour lesquels on effectue l'expérience, obtenant ainsi les valeurs de ${F i}$ pour chacun de ces points. On veillera évidemment à ce que tous les autres paramètres de l'expérience restent constants.

NB : on travaille de préférence avec des variables réduites, c’est-à-dire des variables T, C et m qui sont sans dimensions et normalisées à 1 sur leur intervalle de définition

Il en résulte le système de 10 équations à 10 inconnues:

$F i$ = $a i 1$ $\cdot$ $b 1$ + $a i 2$ $\cdot$ $b 2$ + $a i 3$ $\cdot$ $b 3$ + $a i 4$ $\cdot$ $b 4$ + $a i 5$ $\cdot$ $b 5$ + $a i 6$ $\cdot$ $b 6$ + $a i 7$ $\cdot$ $b 7$ + $a i 8$ $\cdot$ $b 8$ + $a i 9$ $\cdot$ $b 9$ + $a i 10$ $\cdot$ $b 10$

avec $i$ = 1,..,10.

Les $a i j$ sont obtenus simplement en remplaçant $T, C$ et $m$ par leur valeurs aux points où l'on a fait les expériences.

En écriture matricielle:

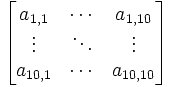
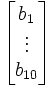
$\begin{bmatrix} F_1 \\ \vdots \\ F_{10} \end{bmatrix}$ = $\begin{bmatrix} a_{1,1} & \cdots & a_{1,10} \\ \vdots & \ddots & \vdots \\ a_{10,1} & \cdots & a_{10,10} \end{bmatrix}$ $\cdot$ $\begin{bmatrix} b_1 \\ \vdots \\ b_{10}\end{bmatrix}$

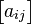
Pour résoudre ce système, il faut inverser la matrice $\begin{bmatrix} a_{ij}\end{bmatrix}$ :

$\begin{bmatrix} b_1 \\ \vdots \\ b_{10} \end{bmatrix}$ = ${\begin{bmatrix} a_{1,1} & \cdots & a_{1,10} \\ \vdots & \ddots & \vdots \\ a_{10,1} & \cdots & a_{10,10} \end{bmatrix}}^{-1}$ $\cdot$ $\begin{bmatrix} F_1 \\ \vdots \\ F_{10}\end{bmatrix}$

La théorie des plans expérimentaux permet à partir de modèles spécifiques plus ou moins complexes de déterminer précisément en quels points les mesures doivent être faites.

En sciences appliquées (plans expérimentaux)

- Introduction - Position du problème - Limites des plans expérimentaux exhaustifs - En sciences appliquées (plans expérimentaux) - Les plans factoriels - Exemple

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭

C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱

Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥

Etude scientifique: ces aliments nous font vieillir 🍽️

Pourquoi notre visage est-il plus petit et délicat que celui des Néandertaliens ? 🤔

A 18 ans, il découvre 1,5 million d'objets célestes inconnus avec son algorithme d'IA 🌟

Que sont ces objets rouges et aplatis, qualifiés d'UFOs par les astronomes ? 🔭

Une méthode simple pour améliorer les performances en mathématiques 🧮

Que sont ces étranges éclairs rouges photographiés au-dessus de l'Himalaya ? ⚡

Nous descendons non pas d'un, mais d'au moins deux groupes anciens 🧬

Un nuage géant de 160 000 soleils découvert dans notre Voie lactée 🔭

Connaissez-vous le rat-kangourou musqué, ce marsupial à la démarche unique ? 🦘

Comment une poignée de traders a fait s'effondrer deux cryptomonnaies 📉

Première cartographie titanesque d'un cerveau, avec 500 millions de connexions neuronales 🧠

Cette double supernovae proche est inexorable, voici la date... qui va vous surprendre 💥

Un océan phosphorescent: comment s'explique ce phénomène rare et féerique ? 🌊

Page générée en 0.127 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise