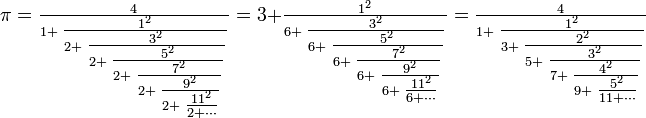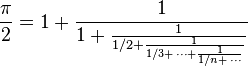Pi - Définition

Propriétés avancées

Approximations numériques

Comme π est transcendant, il n'existe pas d'expression du nombre qui fasse uniquement appel à des nombres et des fonctions algébriques. Les formules de calcul de π utilisant l'arithmétique élémentaire impliquent généralement les sommes infinies. Ces formules permettent d'approximer π avec le moins d'erreur que l'on désire, sachant que plus on rajoute de termes dans le calcul, plus le résultat sera proche de π.

Par conséquent, les calculs numériques doivent utiliser des approximations de π. Dans de nombreux cas, les approximations 3,14 ou 22/7 suffisent, bien que les ingénieurs utilisent souvent 3,1416 (5 chiffres significatifs) ou 3,14159 (6 chiffres significatifs) pour plus de précision. Les approximations 22/7 et 355/113, avec 3 chiffres significatifs et 7 respectivement, sont obtenus à partir de l'écriture en fraction continue de π.

L'approximation de π en 355/113 est la meilleure qui puisse être exprimée avec uniquement 3 ou 4 chiffres au numérateur et au dénominateur, la meilleure approximation suivante étant 103993/33102, qui en exige un nombre beaucoup plus important ; ceci venant de l'apparition du nombre élevé 292 dans le développement en fraction continue de π.

La première approximation numérique de π fut certainement 3. Dans les cas où une situation ne demande que peu de précision, cette valeur peut servir d'approximation convenable. Si 3 est une estimation par défaut, c'est parce qu'il est le rapport entre le périmètre d'un hexagone régulier inscrit dans un cercle et le diamètre de ce cercle.

Fractions continues

La séquence des dénominateurs partiels du développement en fraction continue de π ne fait apparaître aucun schéma évident :

,

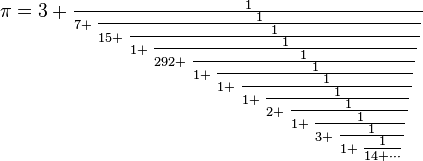
ce qui est une notation équivalente à

Cependant, il existe des fractions continues généralisées représentant π dont la structure est régulière :

π/2 peut aussi être écrit sous une forme de fraction continue généralisée, faisant intervenir la suite des inverses des nombres entiers :

Questions ouvertes

De nombreuses questions se posent encore : π et e sont deux nombres transcendants mais sont-ils algébriquement indépendants ou bien existe-t-il une équation polynomiale à deux variables et à coefficients entiers dont le couple (π, e) soit solution ? La question est encore en suspens. En 1929, Alexandre Gelfond prouve que e^π est transcendant et en 1996, Yuri Nesterenko prouve que π et e^π sont algébriquement indépendants.

Comme dit , on ignore encore si π est un nombre normal, ou même un nombre univers en base 10.